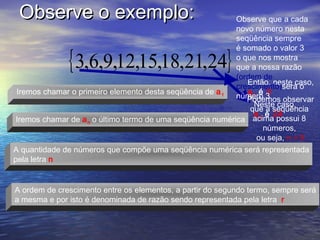
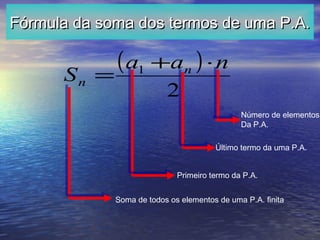
O documento explica o conceito de progressão aritmética, definindo-a como uma sequência numérica onde cada termo subsequente é obtido pela soma de um valor constante ao termo anterior. A fórmula para calcular qualquer termo é apresentada como an = a1 + (n - 1)r, onde a1 é o primeiro termo, n é a posição do termo e r é a razão. A fórmula para calcular a soma dos termos é dada por Sn = (a1 + an)n/2. Exemplos ilustram o uso das fórmulas.

1. PROGRESSÃO ARITMÉTICA
PROFESSORA: MICHELE BOULANGER

2. DEFINIÇÃO
É uma seqüência lógica de informações que
possuem um critério específico e uma ordem
PROGRESSÃO estabelecida para o surgimento de seus
valores. Uma progressão pode ser
crescente ou decrescente
Indica uma relação numérica que será
orientada sobre forma de soma. A aritmética
ARITMÉTICA consiste em realizar operações utilizando o
sistema de contagem na forma de adição.

3. PROGRESSÃO ARITMÉTICA
É uma seqüência numérica orientada
sobre forma de soma onde, cada termo a
partir do segundo, terá um mesmo valor
acrescido em sua seqüência, sendo este
valor o mesmo para todos os elementos e
chamado de razão.

4. Observe o exemplo: Observe que a cada
novo número nesta
seqüência sempre
{ 3,6,9,12,15,18,21,24}
é somado o valor 3
o que nos mostra
que a nossa razão
(ordem de
Então, neste caso,
crescimento)será o
Iremos chamar o primeiro elemento desta seqüência de a 1 a1 é 3
número 3
Podemos observar
Neste caso,
que a seqüência
a n é 24
Iremos chamar de a n o último termo de uma seqüência numérica acima possui 8
números,
ou seja, n = 8
A quantidade de números que compõe uma seqüência numérica será representada
pela letra n
A ordem de crescimento entre os elementos, a partir do segundo termo, sempre será
a mesma e por isto é denominada de razão sendo representada pela letra r

5. Fórmula do termo geral de uma P.A.
an = a1 + ( n − 1) ⋅ r
Razão da P.A.
Número de elementos da P.A.
Primeiro termo da P.A.
Último termo de uma P.A. ou termo procurado

6. Exemplo1:
Determine o 70º elemento de uma P.A. onde o primeiro termo
é 5 e a razão é 8
an = a1 + ( n − 1) ⋅ r
O primeiro procedimento é anotar as informações fornecidas na questão. A partir
O primeiro procedimento é anotar as informações fornecidas na questão. A partir
DADOS:
destas informações iremos desvendar o valor desconhecido utilizando a fórmula
destas informações iremos desvendar o valor desconhecido utilizando a fórmula
do termo geral de uma P.A.
do termo geral de uma P.A.
a1= 5 an = 5 + ( 70 −1) ⋅ 8
Agora basta substituir os valores
fornecidos na questão. Lembre-se
n = 70 que a resolução desta fórmula
r=8 an = 5 + 69 ⋅ 8 segue os princípios de resolução
de uma equação de 1º grau.
an = ?
an = 5 + 552
Utilizamos a interrogação para indicar o valor que desejamos encontrar,
an = 557
ou seja, o último termo desta P.A. que no caso é o 70º elemento.

7. Exemplo2:
Determine o 1º elemento de uma P.A. que possui 120 números
onde o último termo é 570 e a razão é 4
an = a1 + ( n − 1) ⋅ r
Novamente o procedimento é anotar as informações fornecidas na questão para
Novamente o procedimento é anotar as informações fornecidas na questão para
DADOS:
substituir os seus valores na fórmula do termo geral de uma P.A.
substituir os seus valores na fórmula do termo geral de uma P.A.
an= 570
570 = a1 + (120 − 1) ⋅ 4
n = 120
r=4 570 = a1 + 119 ⋅ 4 Neste momento iremos lembrar
do princípio de resolução de
a1 = ? 570 = a + 4761
uma equação onde a letra deve
ficar isolada em um dos lados
570 – 476 =a 1
da equação. Neste caso, o
número +476 irá para o 1º
Utilizamos a interrogação para indicar o valor de desejamos encontrar,
94 = a
ou seja, o primeiro termo desta P.A.membro (antes do sinal de igual) mas,
1 para tanto, é necessário mudar o
sinal de positivo para negativo.

8. IMPORTANTE:
Existem algumas questões que procuram
identificar a soma de todos os termos de
uma P.A. Neste tipo de questão, iremos
levar em conta que esta P.A. representa
um conjunto finito de elementos, ou seja,
podemos definir o primeiro e o último
termo desta seqüência.

9. Fórmula da soma dos termos de uma P.A.
Sn =
( a1 +an ) ⋅ n
2
Número de elementos
Da P.A.
Último termo da uma P.A.
Primeiro termo da P.A.
Soma de todos os elementos de uma P.A. finita

10. Exemplo3:
Determine a soma dos 50 primeiros elementos de uma P.A. onde
o primeiro elemento é 8 e o último 102
(a +a ) ⋅n
Novamente, o procedimento é anotar as informações fornecidas na questão.
Novamente, o procedimento é anotar as informações fornecidas na questão.
DADOS:
Porém, neste caso, a questão deseja saber o valor da SOMA de todos os termos,
S =
Porém, neste caso, a questão deseja saber 1 valor da SOMA de todos os termos,
o n
logo iremos utilizar para esta resolução, a fórmula da soma de elementos de uma
n
logo iremos utilizar para esta resolução, a fórmula da soma de elementos de uma
P.A. finita 2
a=8
P.A. finita
1
( 8 + 102) ⋅ 50
an = 102 S =n
2
n = 50 110 ⋅ 50
Sn =
Sn = ? 2
5500
Sn =
Utilizamos a interrogação para indicar o valor que desejamos encontrar,
2
ou seja, a soma de todos os termos de uma P.A.
S n = 2750

11. Exemplo4:
Determine a soma dos 38 primeiros elementos de uma P.A. onde
a razão é 3 e o primeiro elemento 5.
Neste tipo de questão é preciso se atentar para o que realmente o (problemaquer
a1 +a ) ⋅ n
DADOS: ( )
Neste tipo de questão é preciso se atentar para o que realmente oprobleman quer
= a1 + n − 1 ⋅ r
saber. Observado isto,aede posse da informação que a SOMA = o alvo do
Sn
saber. Observado isto,en de posse da informação que a SOMAserá o alvo do
será 2
nosso cálculo, partimos para outro questionamento: Onde está o valor do último
nosso cálculo, partimos para outro questionamento: Onde está o valor do último
termo desta P.A.?
a=5
termo desta P.A.?
(5 +116 ⋅ 38)
an = 5 + ( 38 − 1) ⋅ 3
1
Sn =
n = 38 2
O valor de a será substituído
r=3 an = 5 + 37 ⋅ 3 Sn =
121 ⋅ 38
n
na fórmula da soma.
an = ? an = 5 + 111 2
4598
Sn = ? Sn =
Neste tipoan = 116 2
de problema, iremos utilizar duas fórmulas para chegar ao
resultado desejado. Primeiro utilizamos a fórmula do termo geral de
= isto, utilizaremos
S Após2299
uma P.A. onde o valor de a será encontrado. n
n
a fórmula da soma dos termos de uma P.A. finita.