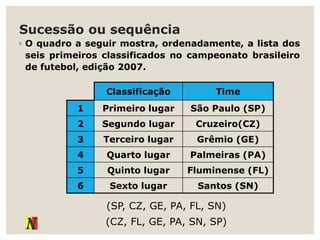
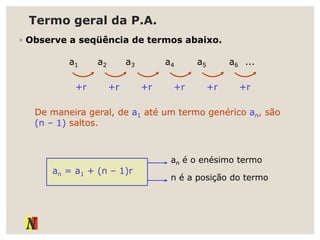
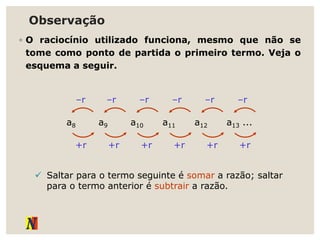
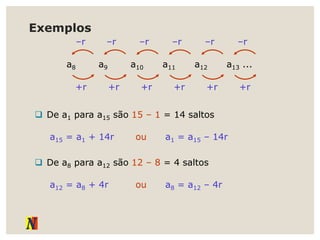
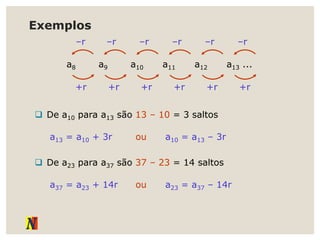
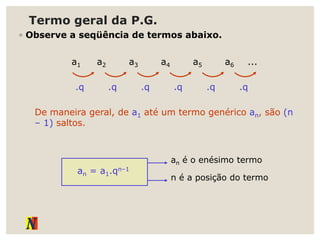
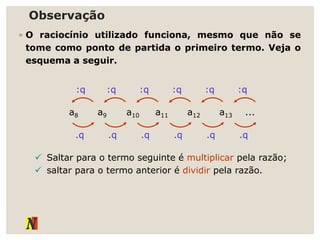
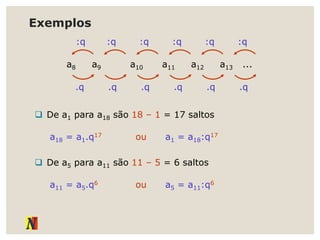
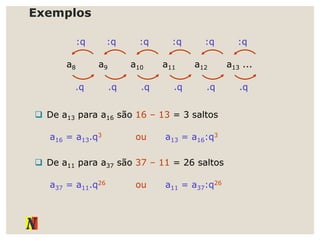
O documento explora progressões aritméticas e geométricas, exemplificando propostas de mesadas entre Denise e Pedro. Ele também discute sequências numéricas, definições, representações e suas aplicações, incluindo leis de recorrência e termos gerais. Adicionalmente, apresenta exemplos práticos de progressões aritméticas e suas somas.