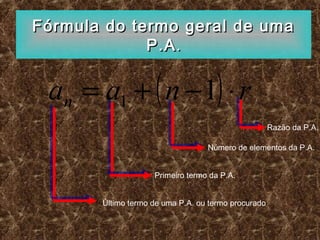
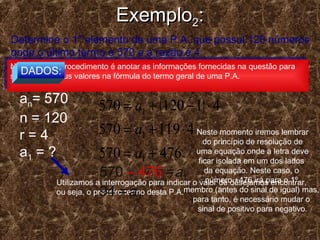
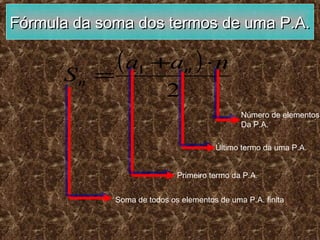
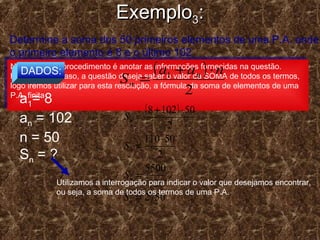
O documento descreve o conceito de sequência e progressão aritmética (P.A). Uma sequência é um conjunto de objetos organizados em ordem definida. Uma P.A. é uma sequência numérica onde cada termo, após o primeiro, é igual à soma do anterior com uma razão constante. O documento fornece fórmulas para calcular termos gerais, soma de termos e determinar termos equidistantes de uma P.A.

1. SequênciasSequências
ouou
sucessõessucessões
Prof. Newton

2. Uma sequência ,ou sucessão , é umUma sequência ,ou sucessão , é um
conjunto de objetos de qualquer naturezaconjunto de objetos de qualquer natureza
organizados ou escritos numa ordem bemorganizados ou escritos numa ordem bem
definida.definida.
Por exemplo, a sequência formada pelosPor exemplo, a sequência formada pelos
números ímpares:números ímpares:
(1;3;5;7;9;....)(1;3;5;7;9;....)
Ou a sequência formada pelos dia daOu a sequência formada pelos dia da
semana:semana:
(domingo; segunda-feira, terça-feira, quarta-(domingo; segunda-feira, terça-feira, quarta-
feira,quinta-feira, sexta-feira, sábado)feira,quinta-feira, sexta-feira, sábado)

3. Uma sequência pode ser classificadaUma sequência pode ser classificada
comocomo finitafinita..
Por exemplo, podemos falar na sequênciaPor exemplo, podemos falar na sequência
dos meses do ano:dos meses do ano:
(Janeiro, fevereiro,março..., dezembro)(Janeiro, fevereiro,março..., dezembro)
EE infinita,,
Por exemplo a sequência dos númerosPor exemplo a sequência dos números
pares escritos em ordem crescente:pares escritos em ordem crescente:
(2,4,6,8,10,12....)(2,4,6,8,10,12....)

4. Para representar uma sequência,Para representar uma sequência,
escrevemos seus elementos, ou termos ,escrevemos seus elementos, ou termos ,
entre parênteses. Por exemplo, paraentre parênteses. Por exemplo, para
representar a sequência dos númerosrepresentar a sequência dos números
pares, fazemos assim:pares, fazemos assim:
(2,4,6,8,10,12,14,...)(2,4,6,8,10,12,14,...)

5. É importante destacar que , ao contrárioÉ importante destacar que , ao contrário
do que ocorre num conjunto, qualquerdo que ocorre num conjunto, qualquer
alteração na ordem dos elementos de umaalteração na ordem dos elementos de uma
sequência altera a própria sequência.sequência altera a própria sequência.
Por exemplo:Por exemplo:
{2,4,6,8}={4,2,8,6}{2,4,6,8}={4,2,8,6}
MasMas
(2;4;6;8)≠(4;2;8;6)(2;4;6;8)≠(4;2;8;6)

6. Uma sequência genérica pode serUma sequência genérica pode ser
representada por:representada por:
(a; a; a; a;...;a;...)(a; a; a; a;...;a;...)
1 2 3 4 n1 2 3 4 n
NoteNote que os índices associados à letraque os índices associados à letra aa
indicam as posições dos termos naindicam as posições dos termos na
sequencia, isto é,sequencia, isto é,

7. a -a - representa o 1° termorepresenta o 1° termo
11
aa -- representa o 2° termorepresenta o 2° termo
22
..
..
..
a -a - representa o n-ésimo termorepresenta o n-ésimo termo
nn

8. Por exemplo, na sequênciaPor exemplo, na sequência
(1;4;9;16;25;36;...)(1;4;9;16;25;36;...)
aa = 1,= 1, a =a = 4,4, aa == 9, a9, a = 16 e assim por= 16 e assim por
1 2 3 41 2 3 4
diante.diante.

9. Três termos consecutivos de umaTrês termos consecutivos de uma
sequência qualquer podem sersequência qualquer podem ser
representados porrepresentados por
a ; a ; aa ; a ; a
n-1n-1 nn n+1n+1
Dizemos também que:Dizemos também que:
aa é o antecessor deé o antecessor de aa
n-1n-1 nn
aa é o sucessor deé o sucessor de aa
n+1n+1 nn

10. Assim, na sequênciaAssim, na sequência
(1;4;9;16;25;36;...)(1;4;9;16;25;36;...)
9 é o9 é o antecessorantecessor de 16 e 25 é ode 16 e 25 é o sucessorsucessor
de 16.de 16.
Determinação de uma sucessão:Determinação de uma sucessão:
As sucessões são dadas, em sua maioria,As sucessões são dadas, em sua maioria,
por meio de uma regra chamadapor meio de uma regra chamada lei delei de
formaçãoformação e que nos permite calculare que nos permite calcular
qualquer termo da sucessão.qualquer termo da sucessão.

11. Exemplos:Exemplos:
Escrever a sucessão em queEscrever a sucessão em que a = 2.na = 2.n ee
nn
nn ЄЄ {1,2,3,4}{1,2,3,4}
Solução:Solução:
aa= 2.1= 2.1 =2;=2;aa= 2.2=4;= 2.2=4;aa== 2.3=6;2.3=6;aa= 2.4= 8= 2.4= 8
1 2 3 41 2 3 4
A sucessão procurada é:A sucessão procurada é:
( 2;4;6;8)( 2;4;6;8)

12. Progressões aritméticas:Progressões aritméticas:
Chama-se progressão aritmética (P.A)Chama-se progressão aritmética (P.A)
toda sequência numérica em que cadatoda sequência numérica em que cada
termo, a partir do segundo, é igual à somatermo, a partir do segundo, é igual à soma
de seu antecessor com um númerode seu antecessor com um número
constante r.constante r.
a = a + r (n ≥ 2)a = a + r (n ≥ 2)
n n-1n n-1
A constante r é a razão da P.AA constante r é a razão da P.A

13. Vejamos estes exemplos:Vejamos estes exemplos:
a) (2 ; 6 ; 10 ; 14 ; 18;...) P.A de razão 4a) (2 ; 6 ; 10 ; 14 ; 18;...) P.A de razão 4
+4 +4 +4 +4+4 +4 +4 +4
b) (5 ; 2 ; -1 ; -4 ; -7 ; ...) P.A de razão -3b) (5 ; 2 ; -1 ; -4 ; -7 ; ...) P.A de razão -3
-3 -3 -3 -3-3 -3 -3 -3
c) (6 ; 6; 6; 6; 6; 6 ;...) P.A de razão 0c) (6 ; 6; 6; 6; 6; 6 ;...) P.A de razão 0

14. Observações!!!!Observações!!!!
Uma P.A. pode ser definida como umaUma P.A. pode ser definida como uma
sequência em que a diferença entre cadasequência em que a diferença entre cada
termo e seu antecessor é constante. Istotermo e seu antecessor é constante. Isto
é,é,
a = a + r a – a = r (n ≥ 2)a = a + r a – a = r (n ≥ 2)
n n-1 n n-1n n-1 n n-1

15. Por exemplo, na p.aPor exemplo, na p.a
(2; 9; 16; 23; 30...) de razão 7(2; 9; 16; 23; 30...) de razão 7
tem-se:tem-se:
aa -- aa = 9 - 2= 9 - 2 aa –– aa = 7= 7
2 1 2 12 1 2 1
aa -- aa = 16 - 9= 16 - 9 aa –– aa = 7= 7
3 2 3 23 2 3 2
aa -- aa = 23 -19= 23 -19 aa –– aa = 7= 7
4 3 4 34 3 4 3

16. Uma p.a de razão r é dita:Uma p.a de razão r é dita:
Crescente , se r › 0Crescente , se r › 0
ex.:ex.: (2 ; 6 ; 10 ; 14 ; 18;...)(2 ; 6 ; 10 ; 14 ; 18;...)
p.a de razão 4p.a de razão 4
Decrescente, se r‹0Decrescente, se r‹0
ex.: (5 ; 2 ; -1 ; -4 ; -7 ; ...)ex.: (5 ; 2 ; -1 ; -4 ; -7 ; ...)
p.a de razão -3p.a de razão -3
Constante, se r=0Constante, se r=0
ex.: (6 ; 6; 6; 6; 6; 6 ;...)ex.: (6 ; 6; 6; 6; 6; 6 ;...)

17. Termo geral de uma P.ATermo geral de uma P.A
O termo geral de uma p.a é dado pelaO termo geral de uma p.a é dado pela
fórmula:fórmula:
a = a + (n-1) . ra = a + (n-1) . r
n 1n 1
Sua tradução para a linguagem comum é aSua tradução para a linguagem comum é a
seguinte:seguinte:
““ Para obter o enésimo termo de uma p.a,Para obter o enésimo termo de uma p.a,
basta somar n-1 vezes à razão aobasta somar n-1 vezes à razão ao
primeiro termo. “primeiro termo. “

18. Por exemplo, para determinar o 10° termoPor exemplo, para determinar o 10° termo
de uma p.a basta somar 9 vezes a razãode uma p.a basta somar 9 vezes a razão
ao 1° termo. Logo, na p.a,ao 1° termo. Logo, na p.a,
(1;4;7;10;13;16;19;...) p.a de razão 3(1;4;7;10;13;16;19;...) p.a de razão 3
Temos:Temos:
aa == a + 9r aa + 9r a == 1 + 9. 31 + 9. 3 .: a.: a=28=28
10 1 1010 1 10
1010
Da mesma forma que ,Da mesma forma que ,
aa == a +50r aa +50r a = 1 + 50.3 .:= 1 + 50.3 .: aa= 151= 151
51 1 5151 1 51
5151

19. Termos equidistantes de umaTermos equidistantes de uma
P.AP.A
Numa sequência finita o primeiro e oNuma sequência finita o primeiro e o
último termo são chamados extremos.Porúltimo termo são chamados extremos.Por
exemplo,1 e 15 são os extremos da p.a,exemplo,1 e 15 são os extremos da p.a,
(1;3;5;7;9;11;13;15)(1;3;5;7;9;11;13;15)
Dizemos que dois termos são de umaDizemos que dois termos são de uma
sequência são equidistantes dossequência são equidistantes dos
extremos se o número de termos queextremos se o número de termos que
antecede um é igual ao número de termosantecede um é igual ao número de termos
que sucedem o outro.que sucedem o outro.

20. Então , na p.a do exemplo dado, temos:Então , na p.a do exemplo dado, temos:
(1;3;5;7;9;11;13;15)(1;3;5;7;9;11;13;15)
Onde os pares de termos 3 e 13, 5 e 11, 7Onde os pares de termos 3 e 13, 5 e 11, 7
e 9 são equidistantes dos extremos.e 9 são equidistantes dos extremos.
Propriedade:Propriedade:
Numa p.a finita, a soma de quaisquer dois
termos equidistantes dos extremos é igual
a soma dos extremos.

21. Utilizando ainda o exemplo dado temos :Utilizando ainda o exemplo dado temos :
(1;3;5;7;9;11;13;15)(1;3;5;7;9;11;13;15)
Onde:Onde:
1 e 15 são os extremos, sua soma é dada1 e 15 são os extremos, sua soma é dada
por: 1+15= 16. A partir daí temos,por: 1+15= 16. A partir daí temos,
3 e 13 , 5 e 11 ,7 e 9 são termos3 e 13 , 5 e 11 ,7 e 9 são termos
equidistantes desta p.a.Sua soma é dadaequidistantes desta p.a.Sua soma é dada
por:por:
3+13 = 5+11 = 7+9 = 1+15 =16.3+13 = 5+11 = 7+9 = 1+15 =16.

22. Soma dos termos de uma p.a finitaSoma dos termos de uma p.a finita
A soma dos n primeiros termos de umaA soma dos n primeiros termos de uma
p.a finita é dada pela fórmula:p.a finita é dada pela fórmula:
s = (a + a). ns = (a + a). n
n 1 nn 1 n
22
Por exemplo:Por exemplo:
Calcular a soma dos 15 primeiros termosCalcular a soma dos 15 primeiros termos
de uma p.a onde,de uma p.a onde, aa = 12 e= 12 e rr= 3= 3
11

23. Solução:Solução:
Antes de calcular a soma temos de acharAntes de calcular a soma temos de achar
aa ..
1515
aa = 12 + 14.3 .:= 12 + 14.3 .: aa =56=56
15 1515 15
Daí a soma dos 15 termos da p.a éDaí a soma dos 15 termos da p.a é
s = (12 + 56) . 15 /2 .:= (12 + 56) . 15 /2 .: ss =510=510
1515 1515

24. Exercícios:Exercícios:
1-Determine o 21°, 73° e 139° termos da1-Determine o 21°, 73° e 139° termos da
p.a (-17,-11;-5;...)p.a (-17,-11;-5;...)
2-calcule o primeiro termo de uma p.a , nos2-calcule o primeiro termo de uma p.a , nos
seguintes casos:seguintes casos:
a) a= 92 e r=3 b) a= 81 e r = -4a) a= 92 e r=3 b) a= 81 e r = -4
34 8134 81
3-Quantos termos possui a seguinte p.a?3-Quantos termos possui a seguinte p.a?
(-19;-15;...;205)(-19;-15;...;205)

25. PROGRESSÃOPROGRESSÃO
ARITMÉTICAARITMÉTICA
PROFESSOR: Newton Lima

26. DEFINIÇÃODEFINIÇÃO
PROGRESSÃO
É uma sequência lógica de informações que
possuem um critério específico e uma ordem
estabelecida para o surgimento de seus
valores. Uma progressão pode ser
crescente ou decrescente!
ARITMÉTICA
Indica uma relação numérica que será
orientada sobre forma de soma. A aritmética
consiste em realizar operações utilizando o
sistema de contagem na forma de adição.

27. PROGRESSÃO ARITMÉTICAPROGRESSÃO ARITMÉTICA
É uma sequência numéricaÉ uma sequência numérica
orientada sobre forma de somaorientada sobre forma de soma
onde, cada termo a partir doonde, cada termo a partir do
segundo, terá um mesmo valorsegundo, terá um mesmo valor
acrescido em sua sequência, sendoacrescido em sua sequência, sendo
este valor o mesmo para todos oseste valor o mesmo para todos os
elementos e chamado de razão.elementos e chamado de razão.

28. Observe o exemplo:Observe o exemplo:
{ }24,21,18,15,12,9,6,3
O primeiro elemento da sequência é chamado de a1
an é o último termo de uma sequência numérica
O número de elementos de uma sequência numérica será
representado pela letra n
A ordem de crescimento entre os elementos, ou razão, a partir do
segundo termo, sempre será a mesma e será representada pela letra
r
Então, neste caso,
a1 é 3
Neste caso,
an é 24
Podemos observar
que a seqüência
acima possui 8
números,
ou seja, n = 8
Observe que a cada
novo número nesta
seqüência sempre
é somado o valor 3
o que nos mostra
que a nossa razão
(ordem de
crescimento)será o
número 3

29. Fórmula do termo geral de umaFórmula do termo geral de uma
P.AP.A..
( ) rnaan ⋅−+= 11
Último termo de uma P.A. ou termo procurado
Primeiro termo da P.A.
Número de elementos da P.A.
Razão da P.A.

30. ExemploExemplo11::
( ) rnaan ⋅−+= 11
Determine o 70º elemento de uma P.A. onde o primeiro termo
é 5 e a razão é 8
O primeiro procedimento é anotar as informações fornecidas na questão. A partir
destas informações iremos desvendar o valor desconhecido utilizando a fórmula
do termo geral de uma P.A.
O primeiro procedimento é anotar as informações fornecidas na questão. A partir
destas informações iremos desvendar o valor desconhecido utilizando a fórmula
do termo geral de uma P.A.
DADOS:
a1= 5
n = 70
r = 8
an = ?
Utilizamos a interrogação para indicar o valor que desejamos encontrar,
ou seja, o último termo desta P.A. que no caso é o 70º elemento.
Agora basta substituir os valores
fornecidos na questão. Lembre-se
que a resolução desta fórmula
segue os princípios de resolução
de uma equação de 1º grau.
( )
557
5525
8695
81705
=
+=
⋅+=
⋅−+=
n
n
n
n
a
a
a
a

31. ExemploExemplo22::
( ) rnaan ⋅−+= 11
Determine o 1º elemento de uma P.A. que possui 120 números
onde o último termo é 570 e a razão é 4
Novamente o procedimento é anotar as informações fornecidas na questão para
substituir os seus valores na fórmula do termo geral de uma P.A.
Novamente o procedimento é anotar as informações fornecidas na questão para
substituir os seus valores na fórmula do termo geral de uma P.A.
DADOS:
an= 570
n = 120
r = 4
a1 = ?
Utilizamos a interrogação para indicar o valor de desejamos encontrar,
ou seja, o primeiro termo desta P.A.
( )
476570
4119570
41120570
1
1
1
+=
⋅+=
⋅−+=
a
a
a
Neste momento iremos lembrar
do princípio de resolução de
uma equação onde a letra deve
ficar isolada em um dos lados
da equação. Neste caso, o
número +476 irá para o 1º
membro (antes do sinal de igual) mas,
para tanto, é necessário mudar o
sinal de positivo para negativo.
570 – 476 =a1
94 = a1

32. IMPORTANTE:IMPORTANTE:
Existem algumas questões que procuram
identificar a soma de todos os termos de
uma P.A. Neste tipo de questão, iremos
levar em conta que esta P.A. representa
um conjunto finito de elementos, ou seja,
podemos definir o primeiro e o último
termo desta seqüência.

33. Fórmula da soma dos termos de uma P.A.Fórmula da soma dos termos de uma P.A.
( )
2
1 naa
S n
n
⋅+
=
Soma de todos os elementos de uma P.A. finita
Primeiro termo da P.A.
Último termo da uma P.A.
Número de elementos
Da P.A.

34. ExemploExemplo33::
Determine a soma dos 50 primeiros elementos de uma P.A. onde
o primeiro elemento é 8 e o último 102
Novamente, o procedimento é anotar as informações fornecidas na questão.
Porém, neste caso, a questão deseja saber o valor da SOMA de todos os termos,
logo iremos utilizar para esta resolução, a fórmula da soma de elementos de uma
P.A. finita
Novamente, o procedimento é anotar as informações fornecidas na questão.
Porém, neste caso, a questão deseja saber o valor da SOMA de todos os termos,
logo iremos utilizar para esta resolução, a fórmula da soma de elementos de uma
P.A. finita
DADOS:
a1= 8
an = 102
n = 50
Sn = ?
( )
2
1 naa
S n
n
⋅+
=
( )
2750
2
5500
2
50110
2
501028
=
=
⋅
=
⋅+
=
n
n
n
n
S
S
S
S
Utilizamos a interrogação para indicar o valor que desejamos encontrar,
ou seja, a soma de todos os termos de uma P.A.

35. ExemploExemplo44::
( ) rnaan ⋅−+= 11
( )
2
1 naa
S n
n
⋅+
=
( )
116
1115
3375
31385
=
+=
⋅+=
⋅−+=
n
n
n
n
a
a
a
a
Determine a soma dos 38 primeiros elementos de uma P.A. onde
a razão é 3 e o primeiro elemento 5.
Neste tipo de questão é preciso se atentar para o que realmente o problema quer
saber. Observado isto, e de posse da informação que a SOMA será o alvo do
nosso cálculo, partimos para outro questionamento: Onde está o valor do último
termo desta P.A.?
Neste tipo de questão é preciso se atentar para o que realmente o problema quer
saber. Observado isto, e de posse da informação que a SOMA será o alvo do
nosso cálculo, partimos para outro questionamento: Onde está o valor do último
termo desta P.A.?
DADOS:
a1= 5
n = 38
r = 3
an = ?
Sn = ?
Neste tipo de problema, iremos utilizar duas fórmulas para chegar ao
resultado desejado. Primeiro utilizamos a fórmula do termo geral de
uma P.A. onde o valor de an será encontrado. Após isto, utilizaremos
a fórmula da soma dos termos de uma P.A. finita.
( )
2299
2
4598
2
38121
2
381165
=
=
⋅
=
⋅+
=
n
n
n
n
S
S
S
S
O valor de an será substituído
na fórmula da soma.

36. Um pouco de exercício!!!Um pouco de exercício!!!

37. Progressão AritméticaProgressão Aritmética
• Determine o primeiro termo de uma PADetermine o primeiro termo de uma PA
onde aonde a33 = 8 e r = -3= 8 e r = -3
an = a1 + (n-1) x r
8 = a1 + (3-1) x (-3)
8 = a1 + 2 x (-3)
8 = a1 + (-6)
8 = a1 -6
a1 = 8+6 14

38. Progressão AritméticaProgressão Aritmética
• Determine a razão da PA(3, 9, 15,...)Determine a razão da PA(3, 9, 15,...)
r = a2
- a1
a2
=9
a1
=3
Dados:
r = 9 – 3
r = 6