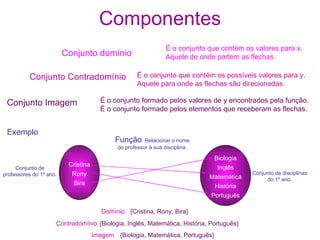
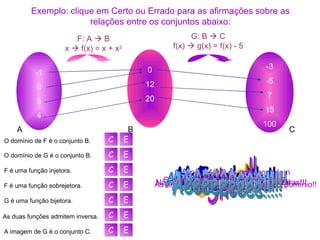
O documento explica os principais conceitos de funções matemáticas, incluindo: conjunto domínio, conjunto contradomínio, conjunto imagem, funções injetoras, sobrejetoras e bijetoras e funções compostas. Um exemplo de função é dado relacionando professores e disciplinas que lecionam.

1. Funções Prof. Cristina Neves 2º Bimestre resumão para estudar

2. Componentes Conjunto domínio Conjunto Contradomínio Conjunto Imagem É o conjunto que contém os valores para x. Aquele de onde partem as flechas. É o conjunto que contém os possíveis valores para y. Aquele para onde as flechas são direcionadas. É o conjunto formado pelos valores de y encontrados pela função. É o conjunto formado pelos elementos que receberam as flechas. Exemplo Cristina Rony Bira Biologia Inglês Matemática História Português Conjunto de professores do 1º ano. Conjunto de disciplinas do 1º ano. Função : Relacionar o nome do professor à sua disciplina. Domínio Contradomínio Imagem {Cristina, Rony, Bira} {Biologia, Inglês, Matemática, História, Português} {Biologia, Matemática, Português}

3. Função Composta Função Injetora Função Sobrejetora Função Bijetora Função Inversa Todos os elementos do domínio devem se corresponder a elementos distintos do contradomínio. Cada x se corresponde a um y diferente. O conjunto imagem é o próprio conjunto contradomínio , sem sobrar nem faltar elementos!! É injetora e sobrejetora ao mesmo tempo. Para uma função ter sua inversa, ela deve primeiro ser bijetora . Invertemos os papéis dos conjuntos domínio e imagem, isto é, quem era domínio passa a ser imagem ( quem era x, passa a ser y ) e quem era imagem passa a ser domínio ( quem era y passa a ser x ). Ocorre quando relacionamos duas ou mais funções ao mesmo tempo, levando em conta os valores já calculados de y. Assim, se temos duas funções, F e G, teremos o seguinte encadeamento: x  f(x)  g(f(x)) Tipos

4. Exemplo: clique em Certo ou Errado para as afirmações sobre as relações entre os conjuntos abaixo: -1 0 3 4 0 12 20 -3 -5 7 15 100 F: A  B x  f(x) = x + x 2 G: B  C f(x)  g(x) = f(x) - 5 A B C O domínio de F é o conjunto B. O domínio de G é o conjunto B. A imagem de G é o conjunto C. F é uma função injetora. F é uma função sobrejetora. G é uma função bijetora. As duas funções admitem inversa. Ops... O domínio de f é o conjunto A. Beleza!!! Issooo!!! Nãããooo!!! As setas partem de B, então ele é o domínio!! Opa!! -1 e 0 se correspondem ao mesmo elemento de B. Show!! Moleza heim!! Se liga!! Todos os elementos de B recebem flechas!! Nã-nã-não!! G não é sobrejetora!! Tá fácil isso!!! Nãããããããoooo!!!! Elas não são bijetoras!!! C E C E C E C E C E C E C E Ai, que orgulho!!! Nada disso, C é o contradomínio de G. Aêêêêêêêêê!!!!!