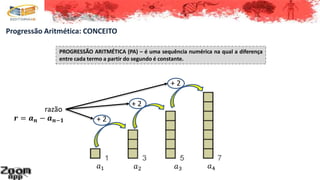
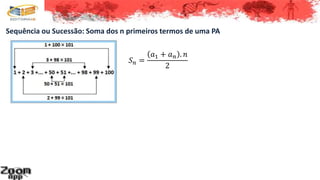
Este documento discute progressões aritméticas, que são sequências numéricas onde a diferença entre cada termo é constante. Ele define progressões aritméticas e explica suas propriedades principais, incluindo como calcular o termo geral, interpolar termos e somar os primeiros termos de uma progressão aritmética.

1. Matemática
Progressão Aritmética

2. Sequências Numéricas:
1. Sequências Numéricas;
a. Sequência ou Sucessão;
b. Leis de Formação;
2. Progressão Aritmética;
a. Conceitos;
b. Razão “r”;
c. Termo Geral;
d. Propriedades de uma PA;
e. Interpolação;
f. Soma dos n primeiros termos de uma PA;
3. Progressão Geométrica;
a. Condição de Existência;
b. Razão “q”;
c. Termo Geral;
d. Propriedades de uma PG;
e. Interpolação;
f. Soma dos n primeiros termos de uma PG;
g. Soma dos Infinitos termos de uma PG.

3. PROGRESSÃO ARITMÉTICA (PA) – é uma sequência numérica na qual a diferença
entre cada termo a partir do segundo é constante.
Progressão Aritmética: CONCEITO
+ 2
+ 2
+ 2
razão
𝑎1 𝑎2 𝑎3 𝑎4
𝒓 = 𝒂 𝒏 − 𝒂 𝒏−𝟏

4. Progressão Aritmética: Termo Geral de uma PA

5. Sequência ou Sucessão: PROPRIEDADES DE UMA PA
Em uma PA de pelo menos 3
termos, podemos obter
qualquer termo , com exceção
dos extremos, como a média
aritmética dos termos
antecedentes e consequentes.
𝑎 𝑛 =
𝑎 𝑛−1 + 𝑎 𝑛+1
2
Em uma PA, a soma de
qualquer valores equidistantes
equivale também a soma dos
extremos.
𝑎 𝑘−1 + 𝑎 𝑘+1 = 𝑎1 + 𝑎 𝑛
Em uma PA de quantidade
ímpar de termos, o termo
médio ou central será a média
aritmética dos extremos.
𝑇. 𝑀 =
𝑎1 + 𝑎 𝑛
2

6. Sequência ou Sucessão: Interpolação Aritmética
Interpolação aritmética – Para interpolar (colocar entre polos ou extremos) n
termos entre dois números 𝑎1 𝑒 𝑎 𝑛, de modo a formar uma PA, deve-se dividir o
intervalo 𝒂 𝒏 − 𝒂 𝟏 em 𝒏 + 𝟏 partes iguais a fim de se obter a razão r.
Exemplo: Dada uma tábua de 35cm deve-se executar 10 furos sendo que o
primeiro e o último devem distar 4cm das extremidades. Qual a distância
entre cada furo intermediário:
𝑎1 = 4𝑐𝑚; 𝑎10 = 31𝑐𝑚.
𝑎10 = 𝑎1 + 𝑛 − 1 . 𝑟 → 31 = 4 + 10 − 1 . 𝑟 → 𝑟 = 3𝑐𝑚

7. Sequência ou Sucessão: Soma dos n primeiros termos de uma PA
𝑆 𝑛 =
𝑎1 + 𝑎 𝑛 . 𝑛
2

8. Fim da Apresentação.