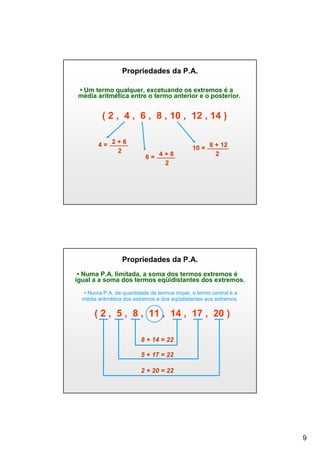
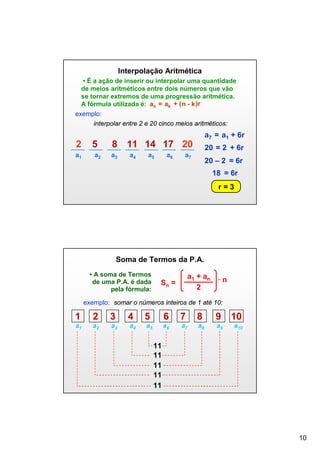
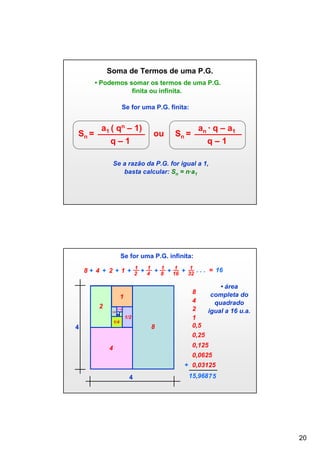
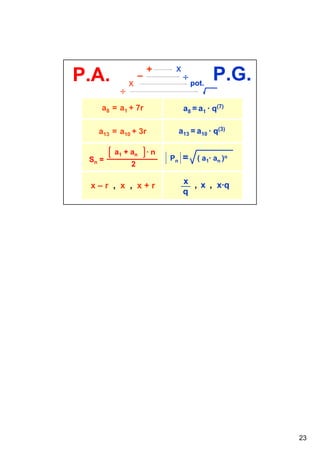
O documento descreve o conceito de sequências numéricas e progressão aritmética (P.A.). As principais informações são: (1) Uma sequência numérica é uma ordem pré-estabelecida de números; (2) Uma P.A. é uma sequência onde cada termo subsequente é igual ao anterior somado a uma constante chamada razão; (3) A fórmula do termo geral de uma P.A. é an = a1 + (n-1)r, onde a1 é o primeiro termo e r é a razão.

1. Seqüências Numéricas
É uma seqüência composta por números
que estão dispostos em uma determinada
ordem pré-estabelecida.
Alguns exemplos de seqüências numéricas:
• (2, 4, 6, 8, 10, 12, ... )
• (0, 1, 2, 3, 4, 5, ...)
• (1, 4, 9, 16, 25, 36, ...)
• (10, 15, 20, 25, 30)
é uma seqüência de números pares
positivos.
é uma seqüência de números
naturais.
é uma seqüência de quadrados
perfeitos.
é uma seqüência de números
múltiplos de 5, maiores que
cinco e menores que 35.
Vale para qualquer seqüência numérica:
(a1, a2, a3, a4, ... , an) seqüência finita.
(a1, a2, a3, a4, ... , an, ... ) seqüência infinita.
primeiro
termo
segundo
termo
terceiro
termo
quarto
termo
enésimo
termo
1

2. Para obtermos os elementos de uma seqüência é preciso
ter uma lei de formação da seqüência.
Por exemplo: an = 2n + 1, n Î N*
Determine os cinco primeiros elementos dessa seqüência:
an = 2n + 1
primeiro termo
n=1
a1 = 21 + 1
a1 = 3
segundo termo
n=2
a2 = 22 + 1
a2 = 5
n=3
23
a3 = 9
terceiro termo
quarto termo
n=4
quinto termo
n=5
a3 =
+1
24
a4 = + 1
a5 = 25 + 1
a4 = 17
a5 = 33
Logo a seqüência será: ( 3, 5, 9, 17, 33, ...)
Progressão Aritmética – P.A.
Observe as seqüências numéricas abaixo:
12
• ( 2, 4, 6, 8, 10, ___ , ... )
r= 2
13
• ( -7, -3, 1, 5, 9, ___ )
r= 4
40
• ( 90, 80, 70, 60, 50, ___, ... )
r = -10
• ( 2, -3, -8, -13, -18, -23 )
___
r = -5
8
• ( 8, 8, 8, 8, 8, ___ , ...)
r= 0
razão positiva
P.A. crescente
razão negativa
P.A. decrescente
razão nula
P.A. constante
Note que as seqüências acima obedecem uma lógica: cada
termo, após o primeiro, é igual ao anterior somado sempre
um mesmo número. Este número é chamado de razão (r).
2

3. Para encontrar a razão de uma P.A.
Basta diminuir qualquer termo de seu anterior:
+r
+r
+r
+r
( 2 , 6 , 10 , 14 , 18, ...)
a1
a2
a3
a4
a5
a2 - a1 = r
a3 - a2 = r
a4 - a3 = r
6–2=4
10 – 6 = 4
14 – 10 = 4
Progressão Aritmética – P.A.
Observe um exemplo de P.A. abaixo:
+r
+r +r
É uma P.A. onde r = 3
+r
( 2 , 5 , 8 , 11 , 14 , ... , ___ , ...)
a1
a2
a3 a4
a5
an
a2 = a1 + ( 1 ) r
a3 = a1 + ( 2 ) r
a17 = a1 + (16 ) r
a4 = a1 + ( 3 ) r
a52 = a1 + ( 51 ) r
Fórmula do
Termo Geral
an = a1 + (n - 1)r
a5 = a1 + ( 4 ) r
a91 = a1 + ( 91 - 1 ) r
a6 = a1 + ( 5 ) r
a91 = a1 + 90∙r
3

4. É uma P.A de razão 6!
a1 = 2
Quanto vale a91?
a91 = a1 + 90r
a91 = 2 + 90(6)
a91 = 2 + 540
a91 = 542
20 26 32 38 44 50 56 62 68
( 2, 8, 14, __, __, __, __, __, __, __, __, __,
__, __, __, __, __, 104 110 116 122 128 134 140
74 80 86 92 98 __, __, __, __, __, __, __,
__, __, __, __, __, __, __, __, __, __, __, __,
146 152 158 164 170 176 182 188 194 200 206 212
218 224 230 236 242 248 254 260 266 272 278 284
__, __, __, __, __, __, __, __, __, __, __, __,
__, __, __, __, __, __, __, __, __, __, __, __,
290 296 302 308 314 320 326 332 338 344 350 356
__, __, __, __, __, __, __, __, __, __, __, __,
362 368 374 380 386 392 398 404 410 416 422 428
__, __, __, __, __, __, __, __, __, __, __, __,
434 440 446 452 458 464 470 476 482 488 494 500
506 512 518 524 530 536 542 548 554 560 566 572
__, __, __, __, __, __, __, __, __, __, __, __,
__, __, __, __, __, __, __,
578 584 590 596 602 608 614 ... )
Termo Geral de uma P.A.
Fórmula do Termo Geral
an = a1 + (n - 1)r
enésimo
termo
razão da
P.A.
primeiro
termo
posição do
enésimo termo
4

5. Exemplo de Exercício de P.A.
Sabendo que uma P.A. tem a1 = 8 e sua
razão é igual a 5, determine a13:
Fórmula do
Termo Geral
an = a1 + (n - 1)r
a13
= a1 + (13 - 1)r
a13 = a1 + 12r
a13 = 8 + 12(5)
a13 = 8 + 60
a13
a13 = 68
( 8, 13, 18, 23, 28, 33, 38, 43, 48, 53, 58, 63, 68, ...)
Progressão Aritmética – P.A.
Pela fórmula do termo geral podemos relacionar qualquer termo
da P.A. com outro termo anterior. Observe:
+r
+r
+r
+r
+r
+r
+r
+r
( 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , ... , ___ , ... )
a1
a2
a3 a4
a7 = a1 + ( 6 ) r
a7 = a5 + ( 2 ) r
a7 = a2 + ( 5 ) r
a5
a6
a7
a8
a9
an
Podemos relacionar quaisquer
dois termos da P.A.
an = ak + ( n - k )r
a7 = a4 + ( 3 ) r
a9 = a3 + ( 6 ) r
5

6. Exemplo de Exercício de P.A.
Sabendo que uma P.A. tem a9 = 22
e a5 = 10 determine sua razão e o
primeiro termo:
an = ak + (n - k)r
a9 = a5 + (9 - 5)r
-2
1
4
7 10 13 16 19 22
a9 = a5 + 4r
a1
a2
a3
a4
22 = 10 + 4r
a5
a6
a7
a8
a9
22 – 10 = 4r
a5 = a1 + (5 - 1)r
12 = 4r
a5 = a1 + 4r
r = 12/4
10 = a1 + 4∙(3)
r=3
10 = a1 + 12
10 - 12 = a1
a1 = - 2
Exercícios de Sala: pág. 2
01) A seqüência (19 – 6x, 2 + 4x, 1 + 6x) são termos consecutivos
de uma P.A. Então o valor de x é:
a3 – a2 = r
19 – 6x
2 + 4x
1 + 6x
a1
a2
a3
a3 – a2 = a2 – a1
(1 + 6x) – (2 + 4x) = (2 + 4x) – (19 – 6x)
1 + 6x – 2 – 4x = 2 + 4x – 19 + 6x
a2 – a1 = r
a3 – a2 = a2 – a1
Para confirmar!
(19 – 6x, 2 + 4x, 1 + 6x)
( 19 – 6·2 , 2 + 4·2 , 1 + 6·2 )
2x – 1 = 10x – 17
( 19 – 12 , 2 + 8 , 1 + 12 )
8x = 16
( 7 , 10 , 13 )
x=2
6

7. Exercícios de Sala: pág. 2
02) Em uma P.A., a5 = 30 e a16 = 118. Calcular a razão da P.A.:
a5 = 30
an = ak + ( n - k )r
a16 = 118
a16 = a5 + ( 16 – 5 )r
118 = 30 + 11r
11r = 118 – 30
11r = 88
r = 88/11
r=8
Exercícios de Sala: pág. 2
03) Determine a razão de uma P.A. com 10 termos, sabendo que
a soma dos dois primeiros é 5 e a soma dos dois últimos é 53?
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10
an = a1 + (n - 1)r
a2 = a1 + r
a1 + a2 = 5
2a1 + r = 5 (-1)
a9 + a10 = 53
a9 = a1 + 8r
2a1 + 17r = 53
a10 = a1 + 9r
a1 + a1 + r = 5
a1 + 8r + a1 + 9r = 53
Fórmula do
Termo Geral
-2a1 – r = -5
+
2a1 + 17r = 53
16r = 48
r=3
7

8. Representações Especiais
Para facilitar a resolução de problemas em P.A. podemos utilizar
os seguintes artifícios:
• para três termos em P.A.
x–r , x , x+r
razão = r
• para quatro termos em P.A.
x – 3r , x – r , x + r , x + 3r
razão = 2r
• para cinco termos em P.A.
x – 2r , x – r , x , x + r , x + 2r
razão = r
Exemplo:
Três números estão em P.A.. A soma deles é 12 e o produto 18.
O termo do meio é:
x–r , x , x+r
(x – r) + (x) + (x + r) = 12
x – r + x + x + r = 12
x + x + x = 12
3x = 12
x = 12/3
x=4
8

9. Propriedades da P.A.
• Um termo qualquer, excetuando os extremos é a
média aritmética entre o termo anterior e o posterior.
( 2 , 4 , 6 , 8 , 10 , 12 , 14 )
4= 2+6
2
6= 4+8
2
10 = 8 + 12
2
Propriedades da P.A.
• Numa P.A. limitada, a soma dos termos extremos é
igual a a soma dos termos eqüidistantes dos extremos.
• Numa P.A. de quantidade de termos ímpar, o termo central é a
média aritmética dos extremos e dos eqüidistantes aos extremos.
( 2 , 5 , 8 , 11 , 14 , 17 , 20 )
8 + 14 = 22
5 + 17 = 22
2 + 20 = 22
9

10. Interpolação Aritmética
• É a ação de inserir ou interpolar uma quantidade
de meios aritméticos entre dois números que vão
se tornar extremos de uma progressão aritmética.
A fórmula utilizada é: an = ak + ( n - k )r
exemplo:
interpolar entre 2 e 20 cinco meios aritméticos:
2
a1
5
a2
a7 = a1 + 6r
8 11 14 17 20
a3
a4
a5
a6
20 = 2 + 6r
a7
20 – 2 = 6r
18 = 6r
r=3
Soma de Termos da P.A.
• A soma de Termos
de uma P.A. é dada
pela fórmula:
a1 + an
2
Sn =
·n
exemplo: somar o números inteiros de 1 até 10:
1
2
3
4
5
6
7
8
9
10
a1
a2
a3
a4
a5
a6
a7
a8
a9
a10
11
11
11
11
11
10

11. Soma de Termos da P.A.
• A soma de Termos
de uma P.A. é dada
pela fórmula:
a1 + an
2
Sn =
·n
exemplo: somar o números inteiros de 1 até 10:
1
2
3
4
5
6
7
8
9
10
a1
a2
a3
a4
a5
a6
a7
a8
a9
a10
a1 = 1
S10 =
a10 = 10
n = 10
S10 =
1 + 10
2
11 · 10
· 10
5
2
S10 = 55
Exercícios de Sala: pág. 5
01) Quantos meios aritméticos devemos interpolar entre 100 e 124
para que a razão seja 4?
100 104 108
a1
112
116
an = ak + ( n - k )r
an = a1 + (n – 1)r
124 = 100 + (n – 1)4
24 = (n – 1)4
24/4 = (n – 1)
6 = (n – 1)
120
124
an
se n = 7 ,
então a P.A.
tem 7 termos,
logo vamos
interpolar 5
meios
aritméticos.
n=7
11

12. (a + b)2 = (a + b)(a + b)
(a + b)2 = a2 + ab + ab + b2
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(a + b)(a – b) = a2 – ab + ab - b2
(a + b)(a – b) = a2 - b2
Exercícios de Sala: pág. 5
02) O perímetro de um triângulo retângulo mede 60m. Sabendo que
seus lados estão em P.A., o valor da hipotenusa, é:
(x – r) + (x) + (x + r) = 60
20 + r
20 – r
x – r + x + x + r = 60
3x = 60
20
(20 +
r)2
400 + 40r +
x = 60/3
= (20 – r)2 + (20)2
r2
= 400 – 40r +
40r = – 40r + 400
r2
x = 20
+ 400
25
15
80r = 400
r=5
20
12

13. Exercícios de Sala: pág. 5
03) Marque no cartão resposta a ÚNICA proposição correta. A
soma dos múltiplos de 10, compreendidos entre 1 e 1995, é:
01. 198.000
02. 19.950
04. 199.000
08. 1.991.010
16. 19.900
1 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 1995
10 20 30
a1
Sn =
1980 = ( n – 1 )10
198 = ( n – 1 )
n = 199
a1 + an
1990
an
·n
2
an = a1 + ( n – 1 ) r
1990 = 10 + ( n – 1 )10
1970 1980
Sn =
10 + 1990
2
· 199
Sn = 2000 · 199
2
Sn = 1000 ∙ 199
Sn = 199000
Progressão Geométrica – P.G.
Observe as seqüências numéricas abaixo:
P.G.
64
• ( 2, 4, 8, 16, 32, ___ , ... )
q= 2
-1
• ( -81, -27, -9, -3, ___ )
q = 1/3
crescente
a1 < 0 e 0 < q < 1
125
• ( 1000, 500, 250, ____ , ... )
q = 1/2
a1 > 0 e 0 < q < 1
• ( -10, -30, -90, -270, -810 )
____
q= 3
P.G.
a1 < 0 e q > 1 decrescente
• ( 5, -10, 20, -40, 80, -160 )
____
q = -2
q<0
P.G. alternante
8
• ( 8, 8, 8, 8, 8, ___ , ...)
q= 1
q=1
P.G. constante
a1 > 0 e q > 1
Observe que cada termo, após o primeiro, é igual ao
anterior multiplicado sempre um mesmo número. Este
número é chamado de razão (q).
13

14. Para encontrar a razão de uma P.G.
Basta dividir qualquer termo de seu anterior:
∙q
∙q
∙q
∙q
( 2 , 4 , 8 , 16 , 32, ...)
a1
a2
a3
a4
a5
a2
=q
a1
a3
=q
a2
a4
=q
a3
4
=2
2
8
=2
4
16
=2
8
Progressão Geométrica – P.G.
Observe um exemplo de P.G. abaixo:
∙q
∙q
∙q
É uma P.G. onde q = 3
∙q
( 1 , 3 , 9 , 27 , 81 , ... , ___ , ...)
a1
a2
a3 a4
a5
a2 = a1 ∙ q ( 1 )
a3 = a1 ∙ q ( 2 )
a12 = a1 ∙ q (11 )
a4 = a1 ∙ q ( 3 )
a61 = a1 ∙ q (60 )
an
Fórmula do
Termo Geral
an = a1 ∙ q ( n - 1 )
a5 = a1 ∙ q ( 4 )
a6 = a1 ∙ q ( 5 )
14

15. Progressão Geométrica – P.G.
Pela fórmula do termo geral podemos relacionar qualquer termo
da P.G. com outro termo anterior. Observe:
∙q
∙q
∙q
∙q
∙q
( 2 , 4 , 8 , 16 , 32 , 64 , ... ___ , ... )
a1
a2
a3
a6 = a1 ∙ q ( 5 )
a6 = a4 ∙ q
a4
a5
a6
an
Podemos relacionar quaisquer
dois termos da P.G.
(2 )
a6 = a2 ∙ q ( 4 )
an = ak ∙ q ( n - k )
a6 = a3 ∙ q ( 3 )
a9 = a5 ∙ q ( 4 )
Exercícios de Sala: pág. 7
01) A seqüência (2x + 5, x + 1, x/2, ...) é uma
progressão geométrica de termos positivos.
O décimo terceiro termo dessa seqüência é:
2x + 5
a1
,
x+1 ,
x/2
a2
a3
(a2)2 = a1 ∙ a3
a2
=q
a1
a3
=q
a2
a2
a
= 3
a1
a2
(a2)2 = a1 ∙ a3
(x + 1)2 = (2x + 5) ∙ ( x )
2
2x + 5 , x + 1 , x/2
2(2) + 5 , (2) + 1 , 2/2
x2 +2x +1 = x2 + 5x
2
9 , 3 , 1 , ...
4x + 2 = 5x
2 = 5x – 4x
x=2
15

16. Exercícios de Sala: pág. 7
Fórmula do
Termo Geral
01) A seqüência (2x + 5, x + 1, x/2, ...) é uma
progressão geométrica de termos positivos.
O décimo terceiro termo dessa seqüência é:
2x + 5
,
x+1 ,
a1
a2
a3
9 ,
3 ,
an = a1 ∙ q ( n - 1 )
x/2
1 , ...
a13 = a1 ∙ q
q = 1/3
a13 = 32 ∙ 3-12
(12)
a13 = 32 + (-12)
a13 = 9 ∙ ( 1 )(12)
3
32
a13 = 32 - 12
3-1
a13 = 3 -10
Exercícios de Sala: pág. 7
a2
=q
a1
02) Determine o número de termos da
P.G. (3, 6, ... , 768):
( 3 , 6 , . . . , 768)
256
128
64
32
16
8
4
2
1
2
2
2
2
2
2
2
2
28
a1
a2
an
an = a1 ∙ q ( n - 1 )
6
=q
3
q=2
768 = 3 ∙ 2( n - 1 )
768 = 2( n - 1 )
3
256 = 2( n - 1 )
A P.G. tem nove termos!
28 = 2( n - 1 )
8=n-1
8+1=n
n=9
16

17. Exercícios de Sala: pág. 7
03) Em uma progressão geométrica
o primeiro termo é 2 e o quarto é
54. O quinto termo dessa P.G. é:
a1 = 2 e a4 = 54
an = a1 ∙ q ( n - 1 )
a4 = a1 ∙ q(4 - 1)
54 = 2 ∙ q3
54
= q3
2
a5 = a4 ∙ q
27 = q3
√27 = q
3
a5 = 54 ∙ 3
a5 = 162
q=3
Representações Especiais
Para facilitar a resolução de problemas em P.G. podemos utilizar
os seguintes artifícios:
• para três termos em P.G.
x , x , x∙q
q
razão = q
• para quatro termos em P.G.
x , x , x∙q , x∙q3
q
q3
razão = q2
17

18. Propriedades da P.G.
• Numa P.G. de três termos (a1, a2, a3) podemos dizer
que o termo central é a média geométrica entre o
anterior (a1) e o posterior (a3), ou seja:
( a1
,
a2
,
a3 )
(a2)2 = a1 ∙ a3
Propriedades da P.G.
• Numa P.G. limitada, o produto dos extremos é igual
ao produto dos termos eqüidistantes dos extremos.
( 2 , 4 , 8 , 16 , 32 , 64 )
8 ∙ 16 = 128
4 ∙ 32 = 128
2 ∙ 64 = 128
18

19. Interpolação Geométrica
• É a ação de inserir ou interpolar uma quantidade
de meios geométricos entre dois números que vão
se tornar extremos de uma progressão geométricos.
A fórmula utilizada é:
(n-k)
an = ak ∙ q
exemplo:
interpolar entre 1 e 243 quatro meios geométricos:
1
a1
3
a2
a6 = a1 ∙ q5
9 27 81 243
a3
a4
a5
243 = 1 ∙ q5
a6
243 = q5
243
√ =q
5
q=3
Produto dos termos de uma P.G.
• O módulo do produto dos termos de uma P.G.
finita é dado pela fórmula:
Pn = (a1∙ an)n
19

20. Soma de Termos de uma P.G.
• Podemos somar os termos de uma P.G.
finita ou infinita.
Se for uma P.G. finita:
Sn =
a1 ( qn – 1)
q–1
ou
an ∙ q – a1
Sn =
q–1
Se a razão da P.G. for igual a 1,
basta calcular: Sn = n∙a1
Se for uma P.G. infinita:
1
1
1
1
1
8 + 4 + 2 + 1 + 2 + 4 + 8 + 16 + 32 . . . = 16
1
2
1/16
1/8
1/2
1/4
8
4
• área
8
completa do
4
quadrado
2
igual a 16 u.a.
1
0,5
0,25
0,125
4
0,0625
+ 0,03125
4
15,968 7 5
20

21. Se for uma P.G. infinita:
Dada uma P.G. em que
0 < | q | < 1, sua soma
pode ser calculada
pela fórmula:
a1
S∞ =
1-q
1
1
1
1
1
8 + 4 + 2 + 1 + 2 + 4 + 8 + 16 + 32 . . . = 16
a1 a2 a3
S∞ =
a1
1-q
a4
a5
S∞ =
a6
a7
8
1-½
sempre que q = ½
Exercícios de Sala: pág. 10
01) A soma de três termos em P.G.
vale 14 e o produto 64. Calcule a
razão dessa P.G.:
x
∙ x ∙ x∙q = 64
q
x∙x∙x∙q
= 64
q
a9 . . .
S∞ =
8
½
S∞ = 16
S∞ = 2∙a1
x
+ x + x∙q = 14
q
4
+ 4 + 4∙q = 14
q
4
+ 4∙q = 10
q
4 + 4q2 = 10q
q
q
x3 = 64
x = 3 64
√
a8
x = 4
4q2 – 10q + 4 = 0 ¸(2)
2q2 – 5q + 2 = 0
se q = ½
se q = 2
8 , 4 , 2
q’ = ½
ou
q” = 2
2 , 4 , 8
21

22. Exercícios de Sala: pág. 10
02) Numa P.G. de 10 termos, sabe-se que S10 = 3069 e que a
razão vale 2, o valor do quinto termo é:
Sn =
S10 =
a1 ( qn – 1)
a1 = 3 e q = 2
q–1
a5 = a1 ∙ q 4
a1 ( 210 – 1)
a5 = 3 ∙ 24
2–1
a5 = 3 ∙ 16
3069 = a1 ( 1024 – 1)
3069 = a1 ( 1023)
3069
= a1
1023
a5 = 48
a1 = 3
Exercícios de Sala: pág. 10
03) A solução da equação: x +
S∞ =
15 =
a1
1-q
x
1-⅓
x
x
x
+
+
+ . . . = 15 é:
27
3
9
• trata-se da soma de
infinitos termos de uma
P.G. onde a1 = x e q = ⅓
15 =
x
⅔
5
15 ∙ 2 = x
3
x = 10
22

23. P.A.
¸
x
–
+
x
¸
pot.
P.G.
a8 = a1 + 7r
a8 = a1 ∙ q(7)
a13 = a10 + 3r
a13 = a10 ∙ q(3)
Sn =
a1 + an
·n
2
x–r , x , x+r
Pn
=
( a1∙ an )n
x , x , x∙q
q
23