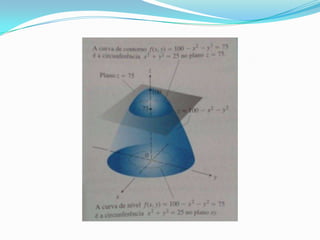
O documento define funções de duas variáveis reais e fornece exemplos para ilustrar conceitos como domínio, imagem e curvas de nível. O primeiro exemplo calcula o valor de uma função para um ponto específico e determina seu domínio e imagem. O segundo exemplo representa graficamente uma função através de curvas de nível e traça três curvas de nível específicas.

1. Isadora G. Toledo
Jacqueline T. Itano

2. Definição
 Suponha que D seja um conjunto de pares ordenados de
números reais (x, y). Uma função real f de duas variáveis
em D é uma regra que associa um único número real
w=f(x,y) a cada par ordenado (x,y) em D. O conjunto D é o
domínio de f, e o conjunto de valores de w assumidos por
f é a sua imagem.
 As variáveis independentes x e y são as variáveis de
entrada da função, e a variável dependente w é a variável
de saída da função.

3. EXEMPLO 1
Seja a função dada por f(x,y) = √x² + y². Determine
f(1,2), Dom f e Im f.
SOLUÇAO:
F (1,2)
f(1,2)= √1² + 2²
f(1,2) = √5

4. Domínio de f
O domínio de uma função de duas variáveis é o
conjunto de pares ordenados do R² para os quais a função
tem sentido, neste caso, para os quais a f(x,y)= √x² + y² é
um número real. Como x² + y² ≥ 0, para qualquer (x ,y) ∈
R², o Dom f = R²

5. Imagem de f
A imagem de f é o conjunto formado pelas imagens
de todos os elementos do domínio de f, neste caso, como
a imagem de qualquer (x,y) ∈ R² par é dada por
f(x,y) = √ x²+y² ≥ 0, a im f = R

6. O gráfico de f é uma superfície do R³ que apareça abaixo:

8. Definição
 Outro método de representar uma função de duas
variáveis geometricamente é similar a representação de
uma paisagem tridimensional por um mapa topológico
bidimensional. Suponha que a superfície Z = f(x,y) seja
interceptada por um plano Z = K e que a curva de
intersecção seja projetada no plano xy. A curva projetada
tem por equação f (x,y) = K e é chamada de curva de
nível.

9. EXEMPLO 2
Represente graficamente f(x,y) = 100 – x² -y² e trace
as curvas de nível f(x,y) = 0, f(x,y) = 51 e f(x,y) = 75 no
domínio de f no plano.
SOLUÇÃO:
O domínio de f é o plano xy inteiro, e a imagem de f
é o conjunto de números reais menores ou iguais a 100. O
gráfico é o paraboloide z = 100 – x² - y².

11. A curva de nível f(x,y) = 0 é o conjunto de pontos no plano
xy nos quais
f(x,y) = 100 – x² - y² = 0,
ou x² + y² = 100,
o qual a circunferência de raio 10 centrada na origem.
Similarmente, as curvas de nível f(x,y) = 51 e f(x,y)=75 são
as circunferências
f(x,y) = 100 – x² - y² = 51,
ou x² + y² = 49
f(x,y) = 100 – x² - y² = 75,
ou x² + y² = 25
A curva de nível f(x,y) = 100 consiste apenas na origem
(Ainda é uma curva de nível.)

13. REFERÊNCIAS BIBLIOGRÁFICAS
 ANTON, Howard. Cálculo: um novo horizonte. 6.ed.
Porto Alegre : Bookman, 2000. 2 v.
 STEWART, J. Cálculo. Vol. I. 4.ed. São Paulo: Pioneira
Thomson Learning, 2003.