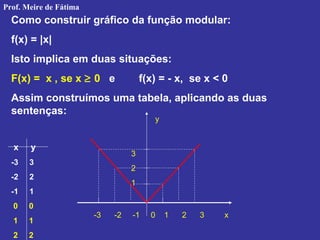
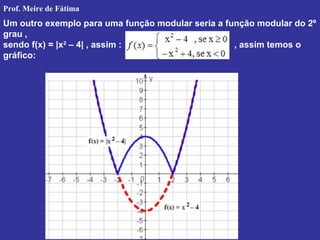
O documento discute funções modulares, definindo módulo como a distância entre dois pontos no eixo real e apresentando propriedades e exemplos de funções modulares como |x|, |x-1|, |x2-4|. Também aborda equações e inequações modulares, mostrando como resolvê-las usando propriedades dos módulos como |x| ≤ a ⇔ -a ≤ x ≤ a.

1. Função modular
• Distância entre dois pontos do eixo real
• Consideremos uma pessoa localizada no ponto A de
abscissa 5 do eixo real, no qual a unidade adotada é o
quilômetro.
Prof. Meire de Fátima

2. -A distância da pessoa, em relação à
origem do referencial é de 5 km.
- Se a pessoa estivesse do outro lado ou
seja na posição –5 km, estaria também a
5 km de distância da origem, só que em
sentido contrário ao positivo ( adotado)
Prof. Meire de Fátima

3. Definição:
• Sejam A e B dois pontos do eixo real com
abscissas xa e x b , e indica-se por d AB ou
d BA a diferença x b - xa
d BA = x b - xa
A B
XA XB
Prof. Meire de Fátima

4. Módulo de um número real
• Módulo de um número real é a distância
entre dois pontos do eixo das abscissas.
• | x | = d AB = x b - xa = 5 – (0) = 5
• | x | = d CA = xA – x c = 0 – (-5) = 5
• | 5 | = 5
• | - 5 | = 5 -5 0 5
C A B
Prof. Meire de Fátima

5. PROPRIEDADES DOS MÓDULOS
• P1- | x | ≥ 0, qualquer que seja x R∈
• P2- | x | = 0 ↔ x = 0
• P3 - | x | = d ↔ x = ± d, com d R∈ +
• P4 - | x | . | y | = | xy | ∀ x, y ∈ R
• P5 - | x | n
= x n
⇒ n é par ∀ x, com x R e n∈ IN∈
P6- 0yeIRy}com{x,y},{x,,
||
||
≠⊂∀=
y
x
y
x
Prof. Meire de Fátima

6. Como construir gráfico da função modular:
f(x) = |x|
Isto implica em duas situações:
F(x) = x , se x ≥ 0 e f(x) = - x, se x < 0
Assim construímos uma tabela, aplicando as duas
sentenças:
x y
-3 3
-2 2
-1 1
0 0
1 1
2 2
-3 -2 -1 0 1 2 3 x
y
3
2
1
Prof. Meire de Fátima

7. Seja f(x) = | x – 1 |
x – 1 ≥ 0 x ≥ 1
| x – 1 | = 0
- ( x – 1 ) < 0
-x +1 < 0
-x < -1
x > 1
Dom(f) = IR
Im(f) = [0, +∞[
1
1
y
x
Prof. Meire de Fátima

8. Um outro exemplo para uma função modular seria a função modular do 2º
grau ,
sendo f(x) = |x2
– 4| , assim : , assim temos o
gráfico:
Prof. Meire de Fátima

9. EQUAÇÕES MODULARES
Observe a seguinte situação:
Uma indústria teve, no ano de 2007, um faturamento de R$ 400.000,00. No ano
de 2008, o faturamento dessa indústria apresentou uma diferença de R$
45.000,00, em relação ao ano anterior. Como não sabemos se a diferença de R$
45.000,00, foi para mais ou para menos. Então chegamos a seguinte situação:
F – 400.000,00 = 45.000,00 ou 400.000,00 – F = 45.000,00
Para representar estas duas equações ( F é a incógnita), podemos utilizar o
módulo considerando a diferença de R$ 45.000,00 como valor absoluto:
| F – 400.000,00| = 45.000,00 que é uma equação com a incógnita em módulo.
Obtemos então duas sentenças e resolvemos as duas:
| F – 400.000| = ± 45.000 F – 400.000 = + 45.000 ou F – 400.000 = - 45.000
F = 45.000 + 400.000 F = - 45.000 + 400.000
F = 445.000 F = 355.000
Assim o faturamento pode ter sido de R$ 445.000,00 ou de R$ 355.000,00
Prof. Meire de Fátima

10. Mais um exemplo:
Resolver a equação | x2
– 5x | = 6
| x2
– 5x | = ± 6
x2
– 5x = + 6
x2
– 5x = - 6
x2
– 5x = + 6 x2
– 5x = - 6
x2
– 5x - 6 = 0
∆= 49
X´ = 6 e x” = -1
x2
– 5x + 6 = 0
∆= 1
X’ = 3 e x” = 2
Logo, S = { -1, 2, 3, 6 }
Prof. Meire de Fátima

11. Agora, observe este exemplo:
|3x-4| ≤ -1
Como 3x – 4 é um número positivo, pois está em módulo, NÃO
HAVERÁ NENHUMA
SOLUÇÃO PARA A SITUAÇÃO ACIMA. POS, NÃO HÁ UM
NUMERO MAIOR QUE ZERO QUE SEJA MENOR OU IGUAL
A -1
ASSIM A SOLUÇÃO É O CONJUNTO VAZIO
S = ∅
Prof. Meire de Fátima

12. CONCLUINDO;
SE a é um número positivo, temos
| x | > a qualquer que seja a pertencente aos
números reais
SE a é um número negativo
|x | > a ⇒ ∀ x ∈ IR ⇒ S = IR
| x | < a ⇒ não existe x ∈ IR ⇒ S = vazio
Prof. Meire de Fátima

13. INEQUAÇÕES MODULARES
As inequações modulares do tipo |f(x)| > a ( ou com as
relações ≥ , ≤ , < ), com a ∈ IR, podem ser resolvidas por
meio das propriedades:
P8- |x| ≤ a ⇔ -a ≤ x ≤ a , ∀ a, com a ∈ I ≤ R.
Exemplo:
| x | ≤ 5 ⇔ -5 ≤ x ≤ 5
P9- |x| < a ⇔ -a < x < a , ∀ a, com a ∈ I ≤ R.
Exemplo:
|x| < 4 ⇔ -4 < x < 4
Prof. Meire de Fátima

14. P10 - |x| ≥ x ⇔ x ≤ - a ou x ≥ a, ∀ a, com a ∈ IR.
Exemplo:
|x| ≥ 6 ⇔ x ≤ -6 ou x ≥ 6
P11-| x | > a ⇔ x < - a ou x > a , ∀ a, com a ∈ IR.
Exemplo:
| x | > 2 ⇔ x < - 2 ou x > 2
Prof. Meire de Fátima

15. Resolver em IR a inequação | 3x –1 | ≤ 8
Pela propriedade P8, temos:
| 3x – 1 | ≤ 8 -8 ≤ 3x – 1 ≤ 8 .
Esta desigualdade é equivalente a:
3x – 1 ≤ 8 ou 3x – 1 ≥ -8
3x ≤ 8 +1 3x ≥ -8 + 1
3x ≤ 9 3x ≥ -7
x ≤ 3 x ≥ -7/3
O conjunto solução S do
sistema è:
-7/3
3
-7/3 3
S = { x ∈ IR / -7/3 ≤ x ≤ 3 }
I
II
I ∩II
Prof. Meire de Fátima

16. Resolver a inequação: | x2
– 5x | > 6
Pela propriedade P11 Temos:
| x2
– 5x | > 6 ⇒ x2
– 5x < - 6 ou x2
– 5x > 6
Resolvendo por Bháskara as duas inequações, obtemos:
x2
– 5x + 6 < 0 ou x2
– 5x - 6 > 0
X’ = 2 ou x” = 3 x’ = -1 ou x” = 6
Prof. Meire de Fátima

17. Agora é com você:
Resolva em IR as inequações modulares:
a) | 3x + 2 | ≥ 5
b) |x2
+ x – 1 | < 1
c) | 2x + 1 | ≤ 2
d) | 3x – 7 | < -1
e) 1 < | x | < 4
Vamos lá você consegue!
Prof. Meire.
Prof. Meire de Fátima