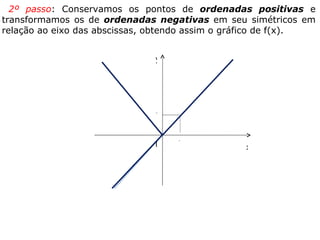
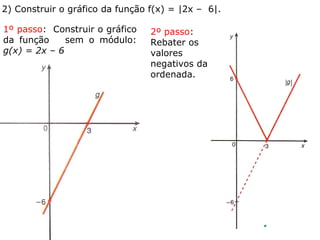
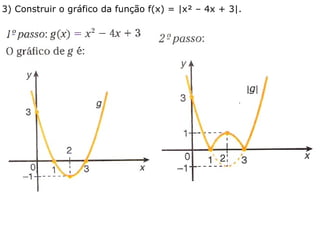
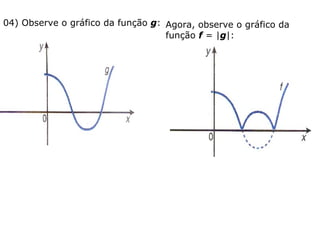
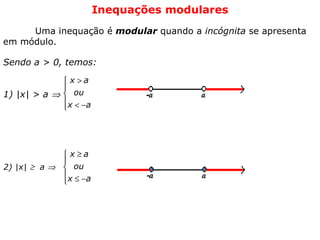
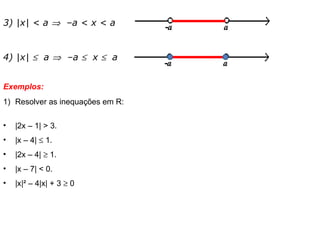
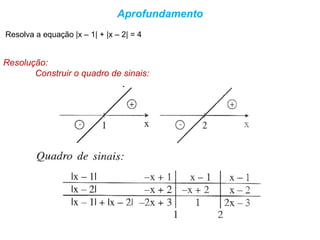
O documento discute o conceito de módulo de um número real, definido como a distância desse número à origem na reta real. Exemplos mostram como calcular o módulo de números e expressões algébricas. Também são apresentados gráficos de funções modulares e resoluções de equações e inequações modulares.

1. MÓDULO DE UM NÚMERO REAL Módulo (ou valor absoluto) de um número O módulo (ou valor absoluto) de um número real x , que se indica por | x | é definido da seguinte maneira: Então: x é positivo ou zero, | x | é igual ao próprio x . Exemplos: | 2 | = 2 ; | 1/2 | = | 1/2 | ; | 15 | = 15. x é negativo, | x | é igual a –x . Exemplos: |–2 | = –(–2) = 2 ; |–20 | = –(–20) = 20.

2. Exemplos: Calcular o valor dos módulos: | | 4 – 3 | – | 6 – 8 | | b) 4 – | 8 + 3 – 16 | c) | | 2 | – | 10 | | 2) Simplificar as expressões: E = | x – 3| + | x – 1|, para x = – 4. b) E = | x³ + x| - | x² - 3x + 1|, para x = – 2.

3. FUNÇÃO MODULAR Denomina-se função modular à função f(x) = |x| definida por: GRÁFICOS Exemplos: 01) Construir o gráfico da função f(x) = |x|. 1º passo : Construir o gráfico da função f sem o módulo. para x = 0, y = 0  (0,0) para x = 1, y = 1  (1, 1) 0 x y 1 1

4. 2º passo : Conservamos os pontos de ordenadas positivas e transformamos os de ordenadas negativas em seu simétricos em relação ao eixo das abscissas, obtendo assim o gráfico de f(x). 0 x y 1 1

5. 2) Construir o gráfico da função f(x) = |2x – 6|. 1º passo : Construir o gráfico da função sem o módulo: g(x) = 2x – 6 2º passo : Rebater os valores negativos da ordenada.

6. 3) Construir o gráfico da função f(x) = |x² – 4x + 3|.

7. 04) Observe o gráfico da função g : Agora, observe o gráfico da função f = | g |:

8. O módulo de um número real é sempre positivo ou nulo. O módulo de um número real nunca é negativo. Representando geometricamente, o módulo de um número real x é igual a distância do ponto que representa, na reta real, o número x ao ponto 0 de origem. Assim: Se | x | < a (com a > 0) significa que a distância entre x e a origem é menor que a , isto é, x deve estar entre – a e a , ou seja, | x | < a  -a < x < a . Se | x | > a (com a > 0) significa que a distância entre x e a origem é maior que a , isto é, deve estar à direita de a ou à esquerda de – a na reta real, ou seja: | x | > a  x > a ou x < – a .

9. Equações modulares Toda a equação que contiver a incógnita em um módulo num dos membros será chamada equação modular . Exemplos: Resolver as equações a seguir: |x – 4| = 6 |2x – 6| = 2 | – x + 2| = – 3 d)|x – 4| = |2x + 1| e)|2x – 6| = |x – 2| f)|2x – 3| = x – 2 g)|4x + 5| = x + 1 h)|x|² – 5|x| + 4 = 0 i)|x|² – |x| – 2 = 0 j) |3x² – x – 1| = 1

10. Inequações modulares Uma inequação é modular quando a incógnita se apresenta em módulo. Sendo a > 0, temos: 1) |x| > a  2) |x|  a 

11. 3) |x| < a  –a < x < a 4) |x|  a  –a  x  a Exemplos: Resolver as inequações em R: |2x – 1| > 3. |x – 4|  1. |2x – 4|  1. |x – 7| < 0. |x|² – 4|x| + 3  0

12. Aprofundamento Resolva a equação |x – 1| + |x – 2| = 4 Resolução: Construir o quadro de sinais:

13. Analisando o quadro de sinais, temos: para x ≥ 2 2x – 3 = 4  x = 7/2 para 1 ≤ x < 2 1 = 4  absurdo para x < 1 – 2x + 3 = 4  x = – 1/2 Analisando as respostas, a 1ª e a 3ª satisfazem as suas respectivas condições de contorno, a 2ª é um absurdo. S = { – 1/2; 7/2}