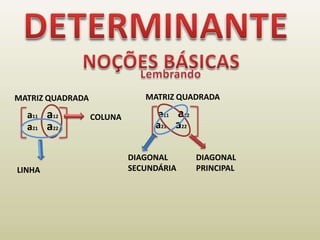
1) Um determinante é calculado para resolver sistemas lineares e está associado a matrizes quadradas. 2) Existem métodos como o de Sarrus e o teorema de Laplace para calcular determinantes de ordem maior. 3) Determinantes possuem propriedades como ser zero se houver linhas ou colunas iguais e mudar de sinal ao trocar linhas/colunas.

1. WGGDETERMINANTE

2. DETERMINANTENOÇÕES BÁSICASUm determinante sempre será associado a uma matriz e sua função e resolver os sistemas lineares ( famosos sistemas) de forma simples. Para calcular um determinante é necessário que a matriz pertencente a ela seja quadrada ou seja i = j ( o número de linhas iguais aos de colunas).DETERMINANTEMATRIZ QUADRADA 2 3 5 67 8 9 2 3 5 67 8 9

3. DETERMINANTENOÇÕES BÁSICASLembrandoMATRIZ QUADRADAMATRIZ QUADRADAa11 a12a11 a12COLUNAa21 a22a21 a22DIAGONALSECUNDÁRIADIAGONALPRINCIPALLINHA

4. DETERMINANTEde ORDEM 2de ORDEM 1( LINHA= 2/COLUNA=2)( LINHA= 1/COLUNA=1)D= 11 23 4 D= -3-3 D= PRODUTO DA DIAGONAL PRINCIPAL – PRODUTO DA DIAGONAL SECUNDÁRIANÃO CONFUNDA COMMODULO, E PARA AINFELICIDADE DETODOS NUNCA CAI EMUMA PROVAD= ( 1 x 4) – ( 3 x 2) = 4 – 6 = -2

5. DETERMINANTEMÉTODO DE SARRUSde ORDEM 3( LINHA= 3/COLUNA=3)2 24 12 1D= PRODUTO DA LINHA + PRODUTO DA LINHA + PRODUTO DA LINHA MENOS PRODUTO DA LINHA + PRODUTO DA LINHA + PRODUTO DA LINHA D= ( 4 + 12 + 8) – (32 +6 + 2) = 24 – 40 = -162 24 12 1CASO VOCÊ ACHE COMPLICADO ESSE JEITO É SÓ REPETIR A PRIMEIRA E A SEGUNDA COLUNA E MULTIPLICA EM LINHA RETA, DANDO O MESMO RESULTADO2 4 2

6. DETERMINANTELEMBRANDO QUE AQUI NÃO PODE SERFEITO PELO MÉTODO PASSADO (MÉTODO DE SARRUS)de ORDEM 4( LINHA= 4/COLUNA=4)2 2 0 0 1 1 0 1 1 2 1 2 2 PARA CONSEGUIRRESOLVER É NECESSÁRIO IRMOS POR PARTESDICA EVITE ELIMINAR LINHA/COLUNA COM UM E/OU ZERO1MENOR COMPLEMENTAR2 2 0 0 1 1 0 1 1 2 1 2 22 2 0 0 1 10 1 1 ELIMINAR UMA LINHA OU COLUNA (À ESCOLHA) REDUZINDO ASSIM A MATRIZ

7. DETERMINANTE2CALCULAR O COFATORi+ jCij= (-1) . DijCALCULAR O COFATORDO ELEMENTO RETIRADO2 2 0 0 1 1 0 1 1 2 1 2 25C41= (-1) . Dij DETERMINANTE DO QUE SOBROU52 2 0 0 1 10 1 1C41= (-1) . Determinante = 0C41= 0

8. DETERMINANTE2CALCULAR O COFATORi+ jCij= (-1) . DijCALCULAR O COFATORDO ELEMENTO RETIRADO2 2 0 0 1 1 0 1 1 2 1 2 25C41= (-1) . Dij DETERMINANTE DO QUE SOBROU52 2 0 0 1 10 1 1C41= (-1) . Determinante = 0C41= 0

9. DETERMINANTE3TEOREMA DE LAPLACEEscolha qualquer linha ou coluna e calcular o Cofator de cada elemento desta 2 2 0 0 1 1 0 1 1 2 1 2 2a41 . A41 + a42 . A42 + a43 . A43 + a44. A442 . A41 + 1 . A42 + 2 . A43 + 2 . A44562 2 0 0 1 1 0 1 1 A41= (-1) . 12 0 3 1 14 1 1 A42= (-1) . 2 -2 = 0 / A41= 0 ( 1 + 8) - ( 6 + 1) = 2A42 = 2

10. DETERMINANTE3TEOREMA DE LAPLACEEscolha qualquer linha ou coluna e calcular o Cofator de cada elemento desta 2 2 0 0 1 1 0 1 1 2 1 2 2a41 . A41 + a42 . A42 + a43 . A43 + a44. A442 . A41 + 1 . A42 + 2 . A43 + 2 . A44782 00 10 1A41= (-1) . 2 20 10 1A42= (-1) . A42 + a44 . A446( 6 ) – (6) = 0 A43 = 0 (8) – (6) = 2 2 . A44 = 4RESPOSTA FINAL

11. DETERMINANTETEOREMA DE JACOBEA META É TRANSFORMAR OS ELEMENTOS EM ZEROS PARA FACILITAR O CÁLCULOSEGUNDO O TEOREMA DE JACOBE, PERMANECENDO UMA LINHA OU COLUNA DA MATRIZ INICIAL E MULTIPLICANDO A OUTRA POR QUALQUER NÚMERO E SOMÁ-LOCOM A PRIMEIRA O DETERMINANTE É O MESMO. MANTÉM A LINHA 15 -232 -9-27 1MULTIPLICA A LINHA 2 POR 5 E SOMA COM A 1D= 19D=19

12. DETERMINANTETEOREMA DE JACOBEA META É TRANSFORMAR OS ELEMENTOS EM ZEROS PARA FACILITAR O CÁLCULOL1L1 -L2L12 1 0 1 1 1 11 0 1 1 2 1 2 22 1 0 0 1 0 -10 2 0 -1 0 3 0 -2L2L2L1 -L3L3L32L1 -L4L4L4 VOCÊ PODE ESCOLHER QUALQUER UMA DESTAS COLUNAS PARA CALCULAR O DETERMINANTE,O IMPORTANTE É CONCENTRAR OS ZEROS EM UMA COLUNA OU LINHAD= a11. A11 - AGORA É SÓ CALCULAR

13. DETERMINANTEPROPRIEDADE DO DETERMINANTE1253 0 145 0 23 1 045 22 0 4545 43 23 22 045 =0=0SE A MATRIZ TIVER UMA LINHA OU UMA COLUNA QUE SÓ HÁ ELEMENTOS ZEROS, SIGNIFICA QUE O DETERMINANTE É ZERO.SE A MATRIZ TIVER DUAS LINHAS OU COLUNAS SEMELHANTES, OU SEJA, IGUAIS, O DETERMINANTE É ZERO.

14. DETERMINANTEPROPRIEDADE DO DETERMINANTE3D= 3 – 2 = 11 0 12 1 1 1 1 1 1 0 12 1 1 1 1 1 2 x SE UMA MATRIZ FOR MULTIPLICADA POR UM NÚMERO QUALQUER O DETERMINANTE TAMBÉM SOFRERÁ A MESMA MUDANÇA.D= 2

15. DETERMINANTEPROPRIEDADE DO DETERMINANTE454 w z0 -k b+9 0 0 1 4 2 1-1 0 9 0 2 1 4 -1 02 0 2 1 9 1= SE ABAIXO OU ACIMA DA DIAGONAL PRINCIPAL SÓ TIVER ZERO, O DETERMINANTE É O PRODUTO DELA. O DETERMINANTE DE UMA MATRIZ E DE SUA TRANSPOSTA SÃO IGUAIS D= -4KDet A = DetAT

16. DETERMINANTEPROPRIEDADE DO DETERMINANTE64 1 2 0 -2 0 0 3 1 0 3 1 0 -2 0 4 1 2 D= -8D= 8SE TROCAR DUAS LINHAS OU DUAS COLUNAS PARALELAS DE LUGAR, O DETERMINANTE MUDA O SINAL

17. DETERMINANTEPROPRIEDADE DO DETERMINANTETeorema de Binet76 15 1 4 10 1 BAD= 1D= 4DetAB = Det A. Det B29 55 1 D= 4  Det A. Det B