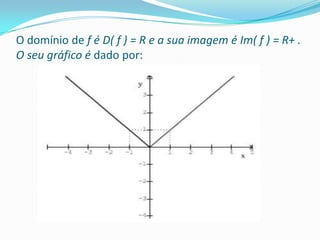
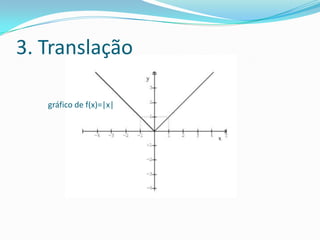
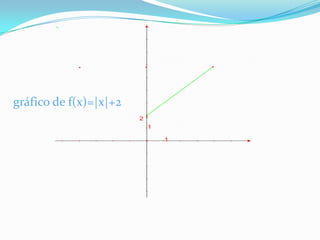
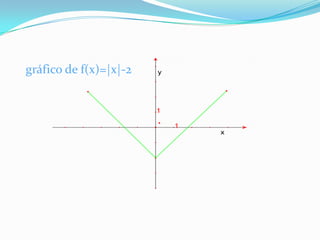
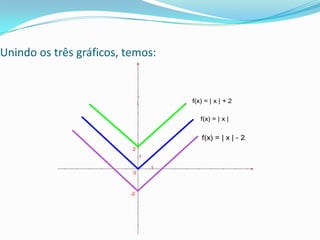
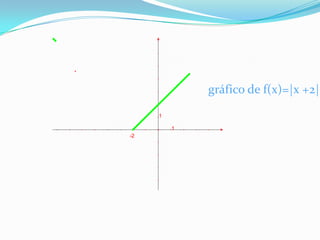
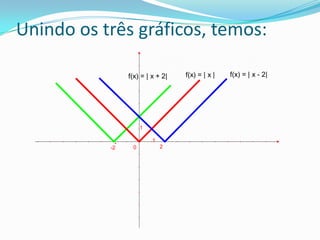
Este documento discute funções modulares e translações gráficas de funções do tipo f(x)=|x|. Explica que a função modular é definida como o valor absoluto de x e tem domínio R e imagem R+. Também mostra como transladar os gráficos de f(x)=|x| para cima ou para baixo adicionando ou subtraindo constantes K, e para a direita ou esquerda adicionando ou subtraindo K ao argumento dentro dos módulos.

1. Função|Modular|Prof. Luciano RibeiroAGOSTO/2010

2. 1. Módulo de um número real• O módulo ou valor absoluto de um número real é o próprio número, se ele for positivo. • O módulo ou valor absoluto de um número real será o seu simétrico, se ele for negativo.

3. |x| = x, se x ≥ 0 -x, se x < 0

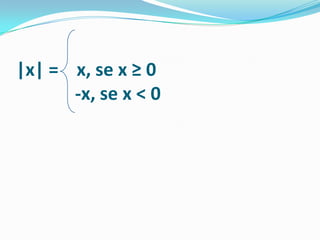
4. Veja alguns exemplos de como calcular módulo ou valor absoluto de números reais. • |+4| = 4 • |-3| = - (-3) = 3 • |10 – 6 | = |+4| = 4 • |-1 – 3| = |-4| = - (-4) = 4 • |-1| + |5| - |6| = -(-1) + 5 – 6 = 1 + 5 - 6 = 6 – 6 = 0 • - | -8| = -[-(-8)] = - 8

5. Veja alguns exemplos de como encontrar o módulo de valores desconhecidos. • |x + 2| nesse caso teremos duas opções, pois não sabemos o valor da incógnita x. Assim, seguimos a definição: x + 2, se x + 2 ≥ 0, ou seja, x ≥ -2 - (x + 2), se x + 2 < 0, ou seja, x < -2 • |2x – 10| 2x – 10, se 2x – 10 ≥ 0, ou seja, 2x ≥ 10 -> x ≥ 5 -(2x – 10), se 2x – 10 < 0, ou seja, 2x < 10 -> x < 5

6. • |x2 – 9| x 2 – 9, se x2 – 9 ≥ 0 x 2 – 9 ≥ 0 x 2 ≥ 9 x ≥ 3 ou x ≤ -3 - (x 2 – 9) , se x2 – 9 < 0 x2 – 9 < 0 x2 < 9 -3 < x < 3

7. 2. Função ModularA função modular, ou função módulo, é a função definida como segue:Da definição de módulo de x, temos que a função modular pode ser definida por duas sentenças :

8. O domínio de f é D( f ) = R e a sua imagem é Im( f ) = R+ . O seu gráfico é dado por:

9. Vamos considerar agora funções definidas por sentenças do tipo1. g(x) = |f (x)|2. g(x) = f (| x|)Exemplos Vamos construir os gráficos das seguintes funções.

14. 3. Translação gráfico de f(x)=|x|

15. gráfico de f(x)=|x|+2

16. gráfico de f(x)=|x|-2

17. Unindo os três gráficos, temos:

18. Conclusões:1) Translação de um gráfico é o deslocamento deste, sobre o plano cartesiano;2) Para a função f(x)= |x|, temos que sua raiz é 0, ou seja o início do gráfico será em y = 0;3) Para a função f(x)= |x|+ K, temos que sua raiz é K, ou seja o início do gráfico será em y = K;4) Para a função f(x)= |x|- K, temos que sua raiz é -K, ou seja o início do gráfico será em y = -K;

19. Vejamos outro tipo de translação;gráfico de f(x)=|x -2|

20. gráfico de f(x)=|x +2|

21. Unindo os três gráficos, temos:

22. Conclusões:1) Para a função f(x)= |x+ K|, temos que sua raiz é -K, ou seja o início do gráfico será em x = -k;2) Para a função f(x)= |x – K|, temos que sua raiz é K, ou seja o início do gráfico será em x = K;

23. Fim"só é vencido aquele que admite a si mesmo que está derrotado”