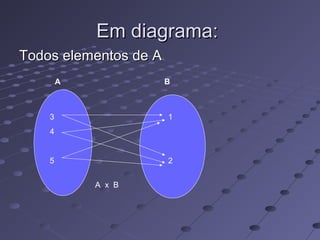
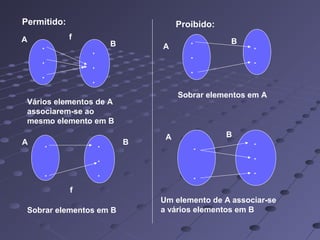
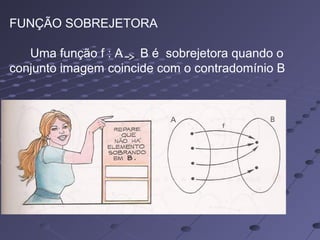
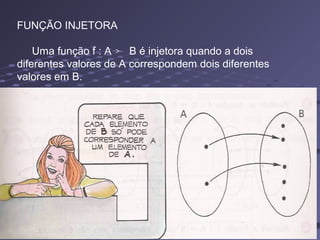
O documento explica os conceitos de produto cartesiano, relação e função. O produto cartesiano de dois conjuntos A e B é formado por todos os pares ordenados com o primeiro elemento de A e o segundo de B. Uma relação é qualquer subconjunto do produto cartesiano, enquanto uma função mapeia cada elemento de A para exatamente um elemento único de B.

1. Produto cartesianoProduto cartesiano
Vejamos primeiramente o conceito deVejamos primeiramente o conceito de
par ordenado:par ordenado:
Dados dois númerosDados dois números xx ee yy numa certa ordem,numa certa ordem,
chamamos de par ordenado ( x,y) ao par dechamamos de par ordenado ( x,y) ao par de
númerosnúmeros xx ee yy ,, tais quetais que xx é o 1º elemento do par eé o 1º elemento do par e
yy é o 2º elemento do par ordenadoé o 2º elemento do par ordenado..
Exemplo: ( 2, 3 )Exemplo: ( 2, 3 ) xx = 2 e= 2 e yy = 3= 3
( - 5 ; 3,2 ) x = -5 e y = 3,2( - 5 ; 3,2 ) x = -5 e y = 3,2
( x, y )( x, y )

2. Produto cartesianoProduto cartesiano
Sendo conhecidos os conjunto A e B:Sendo conhecidos os conjunto A e B:
A = { 3, 4, 5 } e B = { 1, 2 }A = { 3, 4, 5 } e B = { 1, 2 }
A x B = { ( 3,1), (3,2),(4,1),(4,2),(5,1),(5,2)}A x B = { ( 3,1), (3,2),(4,1),(4,2),(5,1),(5,2)}
Produto cartesiano A x B é o produto deProduto cartesiano A x B é o produto de
A por B, formado por pares ordenados onde oA por B, formado por pares ordenados onde o
1º elemento pertence ao 1º conjunto e1º elemento pertence ao 1º conjunto e
o 2º elemento pertence ao 2º conjunto.o 2º elemento pertence ao 2º conjunto.

3. Todos elementos de ATodos elementos de A
3
4
5
1
2
A B
A x B
Em diagrama:Em diagrama:

4. RELAÇÃORELAÇÃO
Dados os conjuntos A e B, qualquerDados os conjuntos A e B, qualquer
subconjunto do produto cartesiano A x B ésubconjunto do produto cartesiano A x B é
chamado dechamado de relaçãorelação de A em B.de A em B.
Sejam os conjuntos A = { 1, 2 } e B = { 1, 2, 3, 4 } e oSejam os conjuntos A = { 1, 2 } e B = { 1, 2, 3, 4 } e o
produto cartesiano A x B.produto cartesiano A x B.
A x B = { (1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4)}A x B = { (1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4)}
Qual é o conjunto dos pares A x B onde o 1ºQual é o conjunto dos pares A x B onde o 1º
elemento é igual ao 2º elemento?elemento é igual ao 2º elemento?
R = { ( 1,1 ), (2,2) } RR = { ( 1,1 ), (2,2) } R ⊂ A x B⊂ A x B

5. Lei de formação:Lei de formação:
Existe uma lei de formação entre osExiste uma lei de formação entre os
conjuntos A e B. No caso do exemploconjuntos A e B. No caso do exemplo
anterior temos:anterior temos:
R = { (x,y) | xR = { (x,y) | x ∈ A, y ∈ B e y = x }∈ A, y ∈ B e y = x }
1
2
1
2
3
4Y = x
A B

6. DOMÍNIO E IMAGEMDOMÍNIO E IMAGEM
Sejam os conjuntos A = { 0, 1, 2, 3} e B = { 1, 2, 4, 5, 6 }Sejam os conjuntos A = { 0, 1, 2, 3} e B = { 1, 2, 4, 5, 6 }
e a relação R de A em B, tal que:e a relação R de A em B, tal que:
R = { { (x, y ) | xR = { { (x, y ) | x ∈∈ A, yA, y ∈∈ B e y = 2 x }B e y = 2 x }
R = { (1, 2 ), (2, 4 ), (3, 6 ) }R = { (1, 2 ), (2, 4 ), (3, 6 ) }
Domínio: { 1, 2, 3 ) primeiros elementos dos paresDomínio: { 1, 2, 3 ) primeiros elementos dos pares
Imagem: { 2, 4 6 } segundos elementos dos paresImagem: { 2, 4 6 } segundos elementos dos pares

7. Relação InversaRelação Inversa
Seja dada a relação R, tal que:Seja dada a relação R, tal que:
R = { (1,3 ), (2, 5 ), ( 3, 8) }R = { (1,3 ), (2, 5 ), ( 3, 8) }
invertendo os valores dos pares obtemosinvertendo os valores dos pares obtemos
a relação inversa de Ra relação inversa de R
RR -1-1
= { (3,1), (5, 2 ), (8, 3 ) }= { (3,1), (5, 2 ), (8, 3 ) }

8. FUNÇÕESFUNÇÕES
Sejam dois conjuntos ASejam dois conjuntos A ≠≠ Ø e BØ e B ≠≠ Ø , e umaØ , e uma
relaçãorelação ff de A em B. Dizemos quede A em B. Dizemos que ff é umaé uma
função ou aplicação de A em B se a todofunção ou aplicação de A em B se a todo
elemento xelemento x ∈∈ A associa-se umA associa-se um únicoúnico elementoelemento
yy ∈B,∈B, tal que o par ( x, y )tal que o par ( x, y ) ∈∈ f.f.
Lemos: f : A BLemos: f : A B
Ou y = f ( x )Ou y = f ( x )

9. Observações:Observações:
1- Toda função é uma relação1- Toda função é uma relação
2- Nem toda relação é uma função.2- Nem toda relação é uma função.
Vamos verificar os casos:Vamos verificar os casos:

10. Permitido:
f
.
.
.
.
.
.
Vários elementos de A
associarem-se ao
mesmo elemento em B
.
.
.
.
.
f
Sobrar elementos em B
A
B
A B
Proibido:
A
B
Sobrar elementos em A
.
.
.
.
.
.
.
.
.
.
A B
Um elemento de A associar-se
a vários elementos em B

11. .. Domínio:Domínio:
É o conjunto de partida das flechas ( A ),É o conjunto de partida das flechas ( A ),
são os valores de x na função.são os valores de x na função.
.. Contradomínio:Contradomínio:
É o conjunto de chegada das flechas ( B ),É o conjunto de chegada das flechas ( B ),
são todos os valores de B.são todos os valores de B.
.. Imagem:Imagem:
São as respostas encontradas para o y.São as respostas encontradas para o y.
Imagem pode ser uma parte ou igual aoImagem pode ser uma parte ou igual ao
conjunto Bconjunto B

12. FUNÇÃO SOBREJETORA
Uma função f : A B é sobrejetora quando o
conjunto imagem coincide com o contradomínio B

13. FUNÇÃO INJETORA
Uma função f : A B é injetora quando a dois
diferentes valores de A correspondem dois diferentes
valores em B.

14. FUNÇÃO BIJETORA
Uma função f : A B é bijetora quando é sobrejetora e
injetora ao mesmo tempo, ou seja quando a cada elemento
de A corresponde um único elemento em B

15. Elaboração;Elaboração;
Meire de Fátima MoralezMeire de Fátima Moralez