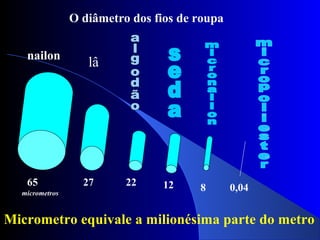
O documento explica como escrever números muito grandes ou muito pequenos usando notação científica. A notação científica expressa um número como o produto de um número entre 1 e 10 por uma potência de 10. Isso torna mais fácil lidar com cálculos envolvendo números de diferentes escalas.

2. A distância média da Terra ao Sol é
de 150 000 000 km.
( Cento e cinquenta milhões de
quilômetros )
Como escrever essa distância usando
notação científica?

3. Na escrita em forma de notação
científica, um dos fatores deve ser
um número entre 1 e 10 e o outro
fator deve ser uma potência de 10.
Assim 150 000 000 = 1,5 . 108
1,5 esta entre 1 e 10
108
é uma potência de 10

4. Conforme publicado em um relatório do
Fundo das Nações Unidas para a
população, no ano 2003 havia 608 milhões
de pessoas, vivendo em 31 países, que
enfrentavam uma crise gerada pela falta
de água. O relatório também informava
que, se nada fosse feito, esses números
seriam alterados para 3 bilhões e 500
milhões de pessoas em 48 países no ano de
2005.

5. 608 milhões = 608 000 000 = 6,08 . 108
3 bilhões e 500 milhões = 3 500 000 000 =
3,5 . 109

6. 65 27 22 12 8 0,04micrometros
O diâmetro dos fios de roupa
lâ
nailon
Micrometro equivale a milionésima parte do metro

7. Graças as novas tecnologias, os fios dos tecidos
estão diminuindo ao longo do tempo.
Para se ter uma ideia, em 1939 os fios de
naylon tinham 0,00065 m de diâmetro.
Atualmente, estes fios tem cerca de
0,000 000 04 m de diâmetro.
É com poderosos microscópios que
conseguimos ver coisas aparentemente
invisíveis a olho nu.

8. Números macroscópicos, ou astronômicos:
-A distância da terra ao sol: 150 000 000 km.
-A massa do Sol:
-1 983 000 000 000 000 000 000 000 000 000 kg.
-A velocidade da luz: 300 000 km/s
-O número de glóbulos vermelhos em 1 litro de
sangue humano: 5 000 000 000.
-Um ano-luz ( unidade de medida astronômica):
9 600 000 000 000 km.

9. Números microscópicos:
-A massa do átomo de hidrogênio:
- 0,000 000 000 000 000 000 000 016 g.
-O diâmetro de uma molécula grande:
-0, 000 000 17 cm.
-A carga de um elétron:
- - 0,000 000 000 000 000 000 16 C ( Coulomb).
-A massa de uma ameba: 0,000 005 g.

10. Se foi difícil para você ler estes
números, imagine efetuar cálculos com
eles.
Mas isto é possível, e vamos nos
deparar com várias situações deste tipo
ao longo deste curso.
O que vai nos ajudar muito é a escrita
em forma de notação científica:

11. Observe alguns exemplos:
100 = 102
1000 = 103
2000 = 2 . 1000 = 2 . 103
23 400 000 = 2,34 . 10 7
(vírgula caminha para a esquerda =
expoente positivo)
2467,8 = 2,4678 . 103
a vírgula andou três
casas até o número 2

12. 0,1 = = 10-1
0,001 = = 10-3
0,00001 = 10 –5
a vírgula andou 5 casas
para a direita
0,023 = 2,3 . 10-2
( 2,3 está entre 1 e 10 )
10
1
1000
1
3
10
1

13. Conclusão:
-Para escrever um número em notação científica,
basta:
-Andar com a vírgula: (expoente negativo)
(expoente positivo)
A parte inteira ( primeiro fator) é um número
entre 1 e 10.
10 4
= 1 . 10 4
= 10000
10 - 4
= 1. 10 - 4
= 0,0001

14. Massa do próton 1,673 .10 - 24
g
Massa do nêutron 1,675 . 10 - 24
g
Massa do elétron 9,11 . 10 -28
g
A massa do próton é cerca de 1836 vezes
maior que a do elétron.
Observe os exemplos:

15. Diâmetro de um átomo = 0,1 nanômetro
O diâmetro de um átomo é da ordem de
10 - 8
cm, enquanto que o de seu núcleo é de
cerca de 10 - 12
cm
O diâmetro da eletrosfera de um átomo é de
10 000 a 100 000 vezes maior que o diâmetro
de seu núcleo

16. Observe estas operações:
multiplicação
12 000 000 000 . 4 000 000 = 1,2 . 1010
. 4 . 10 6
= 1,2 . 4 . 1010
. 10 6
= 4,8 . 1016
Multiplicamos os números ( 1,2 vezes 4)
Conservamos a base 10 e somamos os
expoentes 1010
. 10 6
( ) ( )16610
1010 =
+
( ) ( )16610
1010 =
+

17. 0,0000023 . 0,004 . 10 5
= 2,3 . 10 –6
. 4 . 10-3
. 105
= 2,3 . 4 . 10 –6
. 10-3
. 105
= 9,2 . 10 –4

18. 0,002 . 105
: 200 . 10-4
= 2 . 10-3
. 10 5
: 2 . 102
. 10-4
= 2 . 102
: 2 . 10 –2 (conserva a
base e subtrai os expoentes)
= 1 . 102-(-2)
= 104
Divisão:
Dividimos os números 2:2 = 1

19. Potência de potência
( )( ) ( ) ( )63.232
444 ==
Conserva-se a base e multiplica-se os
expoentes.
Cuidado!
( )( ) ( )
3
232
44 ≠
( )( ) ( )
( ) ( )82
632
44
44
3
=
=

20. 1 mol tem aproximadamente 6,022 × 1023
entidades.
carga do elétron = 1,60217646 × 10-19
C
coulombs
Valores que utilizamos em forma de
notação científica:

21. Na Era do computador:
1 kilobyte equivale a 1024 bytes
1 megabyte equivale a 1 048 576 bytes.
Expresse estes números em forma de
notação científica, arredondando estes
valores

22. Resposta:
1 KB = 1 . 103
b
1 MB = 1,05 . 106
b

23. Fazendo junto:
Escreva os valores abaixo em forma de
notação cientifica:
a) 0,00000012
b) 145 000 000 000
c) 12,34 . 103
d) 0,000 18 . 10-3
e) 125,18
f) 12 000

24. Resolva utilizando notação científica:
1- 4 000 000 000 . 32 000 000 000 000 =
2- 12 . 108
. 1430 . 10 9
=
3- 32 . 10 –7
: 16 . 10 –5
=
4- 12,34 . 10-3
. 15,0 . 100
=
5- 52,3 . 10 + 0,008 . 10
6- 155,8 . 10-4
– 132,3 . 10-4
7- ( 0,03 . 10-2
)2

25. Respostas:
1- 1,28 . 1023
2- 1,716 . 1021
3- 2 . 10 – 2
4- 1,849 . 101
5- 523,08 = 5,2308 . 10-2
6- 0,00235 = 2,35 . 10-3
7- 9 . 10-8
Se acertou todas, você é mesmo fera.

26. NÃO ESQUEÇA:NÃO ESQUEÇA:
Para melhor entendimento, revise sempre
as propriedades e suas aplicações!
Bons estudos.
 Prof. Meire de Fátima
 2012