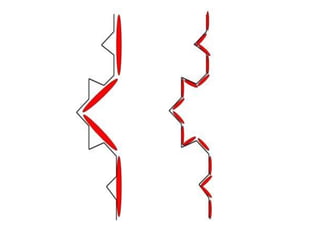
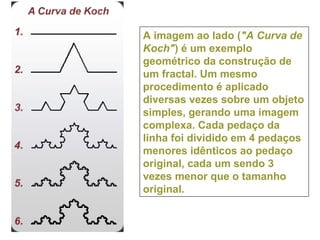
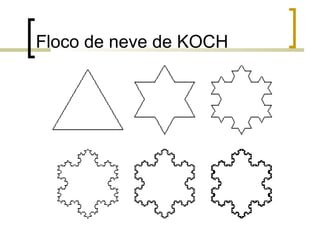
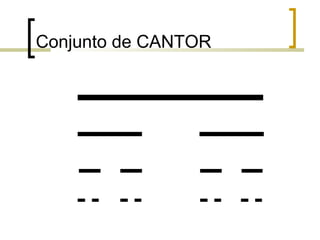
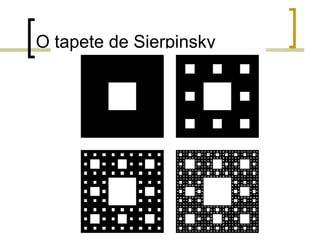
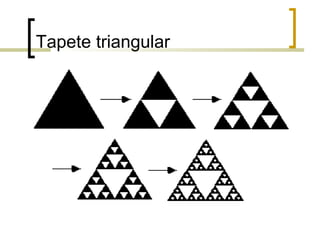
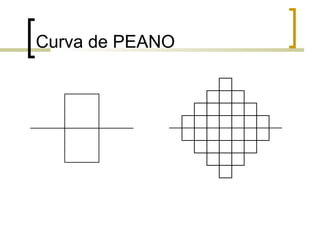
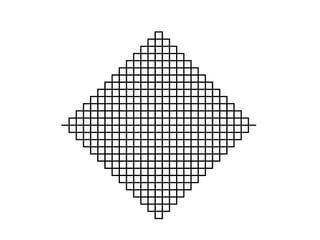
1) Fractais são objetos gerados pela repetição de um mesmo processo recursivo, apresentando auto-semelhança e complexidade infinita.
2) A geometria fractal pode ser usada para descrever fenômenos na natureza como nuvens, montanhas e vasos sanguíneos que não se encaixam na geometria euclidiana.
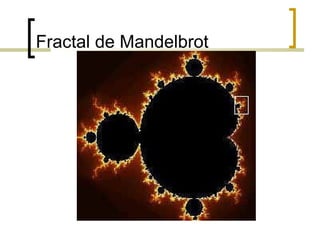
3) Benoît Mandelbrot foi o pioneiro na investigação da geometria fractal e criou o fractal que leva o seu nome, mostrando a auto-semelhança em diferentes escalas.