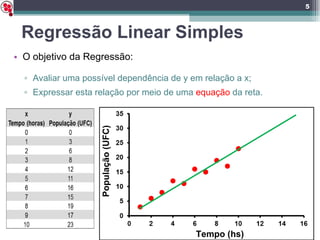
O documento descreve regressão linear simples, que analisa a relação entre duas variáveis quantitativas. Explica que a regressão linear prevê valores de uma variável dependente (y) com base em uma variável independente (x) usando uma equação da reta y = a + bx. Fornece exemplos e detalha como calcular os coeficientes a e b da reta de regressão e testar sua significância estatística.

1. Monica Lima Doutoranda em Neurociências e Biologia Celular [email_address] monicalima@ufpa.br Junho - 2011 Universidade Federal do Pará Instituto de Ciências Biológicas Laboratório de Neuroendocrinologia Faculdade de Ciências Biológicas Regressão Linear Simples

8. Regressão Linear Simples

14. Junho - 2011 Universidade Federal do Pará Instituto de Ciências Biológicas Laboratório de Neuroendocrinologia Faculdade de Ciências Biológicas http://www.slideshare.net/monica_lima/regressão-linear-simples [email_address]