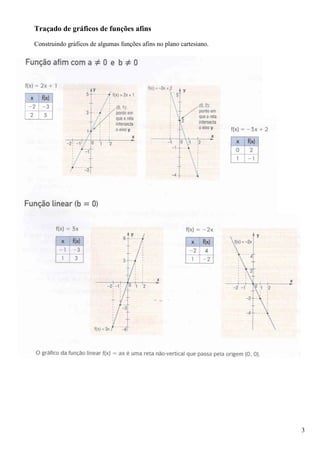
1. O documento descreve as funções afins, que são funções da forma f(x)=ax+b, onde a e b são números reais. 2. Exemplos de funções afins incluem funções lineares, constantes, identidade e translação. 3. O valor de uma função afim em um ponto x é calculado como f(x)=ax+b e exemplos são fornecidos.

1. 1
Função Afim
Definição:
Uma função f: IR → IR (f de IR em IR) chama-se
função afim quando existem dois números reais a e
b tal que f(x) = ax + b, para todo x є IR.
Exemplos:
1) f(x) = 2x + 1 (a = 2, b = 1)
2) f(x) = -x + 4 (a = -1, b = 4)
3) f(x) =
3
1
x + 5 (a =
3
1
, b = 5)
4) f(x) = 4x (a = 4, b = 0)
Valor de uma função afim
Na função afim f(x) = 5x + 1, podemos determinar:
f(1) = 5 • 1 +1 = 5 + 1 = 6. Logo, f(1) = 6.
f(-3)=5(-3) + 1 = -15 + 1 = -14. Logo, f(-3) = -14.
Casos particulares importantes da função afim
1ª) Função linear
f: IR → IR definida por f(x) = ax para todo x є IR. Nesse caso, b = 0.
Exemplos:
• f(x) = -2x (a= -2, b = 0)
• f(x) =
5
1
x (a =
5
1
, b = 0)
• f(x) = 3 x (a = 3 , b = 0)
2ª) Função constante
f: IR → IR definida por f(x) = b para todo x є IR. Nesse caso, a = 0.
Exemplos:
• f(x) = 3
• f(x) = -2
• f(x) = 2
• f(x) =
4
3
3ª) Função identidade
f: IR → IR definida por f(x) = x para todo x є IR. Nesse caso, a = 1 e b = 0.
• f(x) = x

2. 2
4ª) Translação
f: IR → IR definida por f(x) = x + b para todo x є IR. Nesse caso, a = 1 e b ≠ 0.
Exemplos:
• f(x) = x + 2
• f(x) = x - 3
• f(x) = x +
2
1
• f(x) = x -
5
3
Determinação de uma função afim conhecendo-se seus valores em dois
pontos distintos
Uma função f(x) = ax + b fica inteiramente determinada quando conhecemos dois
valores f(x1) e f(x2) para quaisquer x1 e x2 reais, com x1 ≠ x2 . Ou seja, com esses dados
determinamos os valores de a e de b.
Por exemplo, escreva a função afim f(x) = ax + b, sabendo que:
f(1) = 5 e f(-3) = -7
• se f(1) = 5 , então para x = 1 tem-se:
f(x) = ax + b f(1) = 5 f(1) = a · 1 + b
x = 1 5 = a + b
a = ?
b = ?
Ou seja, a + b = 5.
• se f(-3) = -7 , então para x = -3 tem-se:
f(x) = ax + b f(-3) = -7 f(-3) = a · (-3) + b
x = -3 -7 = -3a + b
a = ?
b = ?
Ou seja, -3a + b = -7.
Determinamos os valores de a e b resolvendo os sistema de equações:
a + b = 5 - a – b = - 5 (multiplica-se a equação por -1.)
-3a + b = -7 -3a + b = -7
-4a = -12
a =
4
12
−
−
a = 3
Como a + b = 5 e a = 3, então:
a + b = 5
3 + b = 5
b = 5 – 3 b = 2
Logo a função afim f(x) = ax + b tal que f(1) = 5 e f(-3) = -7 é dada por f(x) = 3x + 2.

3. 3
Traçado de gráficos de funções afins
Construindo gráficos de algumas funções afins no plano cartesiano.

4. 4
Função Identidade (a = 1 e b = 0)
Translação (a = 1 e b ≠ 0)

5. 5
Função constante (a = 0)
Função afim crescente e decrescente
1º Caso: a > 0.
Vamos construir, o gráfico da função f(x) = 2x -1.

6. 6
2º Caso: a < 0.
Vamos construir, o gráfico da função f(x) = -3x -1.

7. 7
Exercícios Propostos
1) Classifique as funções abaixo em afim, linear, identidade, constante e translação:
a. f(x) = 5x + 2
b. f(x) = -x + 3
c. f(x) = 7
d. f(x) = x
e. f(x) = 3x
f. f(x) = x + 5
g. f(x) = -3
h. f(x) =
7
1
x
i. f(x) =
2
x
+
3
1
j. f(x) = 2 – 3x
2) Dada a função f(x) = -2x + 3, determine:
a. f(1)
b. f(0)
c. f 





3
1
d. f 





−
2
1
3) Dada a função afim f(x) = 1 -
2
5
x, calcule.
a. f(0)
b. f(-1)
4) Determine o que se pede.
a. Sabendo que f(x+1) = 2x, calcule f(4).
b. Dada a função f(5x -1) = x -
5
1
, calcule f(0).
5) Sendo f(x) = 3x – 4 e g(x) = 2x + 1, determine os valores reais de x para que se
tenha f(x) < g(x).
6) Dada a função afim f(x) = 2x + 3, determine os valores reais de x para que:
a. f(x) = 1
b. f(x) = 0 c. f(x) =
3
1
d. f(x) = 0,75
7) Na produção de peças, uma indústria tem um custo fixo de R$ 8,00 mais um custo
variável de R$ 0,50 por unidade produzida. Sendo x o número de unidades
produzidas:
a. Escreva a lei da função que fornece o custo total de x peças;
b. Calcule o custo de 100 peças;
c. Escreva a taxa de crescimento da função.
8) Uma pessoa tinha no banco um saldo positivo de R$ 560,00. Após um saque no
caixa eletrônico que fornece apenas notas de R$ 50,00, expresse a lei da função que
fornece o novo saldo, que é dado em função do número x de notas retiradas.
9) Determine o valor da função afim f(x) = -3x + 4 para:
a. x = 1
b. x =
3
1
c. x = 0
d. x = 1,5
e. x = k +1
f. x = a + b

8. 8
10) Escreva a função afim f(x) = ax + b, sabendo que:
a. f(-1) = 7 e f(2) = 1
b. f(2) = -2 e f(1) = 1
11) Dada a função f(x) = ax + b e sabendo que f(3) = 5 e f(-2) = -5, calcule f 





2
1
.
12) Dada a função f(x) = ax + 2, determine o valor de a para que se tenha f(4) = 22.
13) Construa, num sistema ortogonal, o gráfico das seguintes funções, dizendo em cada
caso se a função é crescente ou decrescente:
a. f(x) = x + 2
b. f(x) = - x + 2
c. f(x) = 1 + 2x
14) Faça o gráfico das funções f(x) = x, g(x) = x + 1 e h(x) = x – 2.
15) Construa o gráfico das funções:
a. f(x) = x e g(x) = -x
16) Escreva a função f(x) = ax + b cujo gráfico, num sistema cartesiano ortogonal, é
dado por:
a.