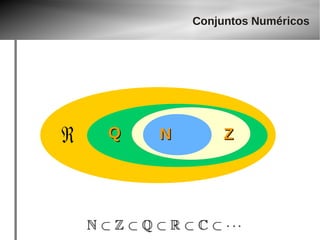
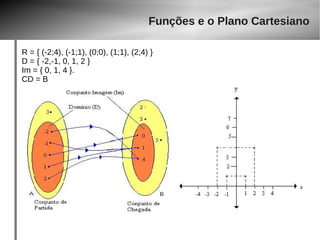
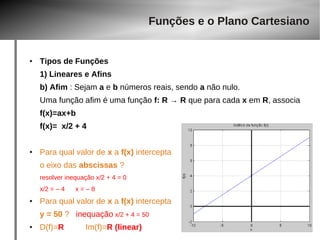
O documento discute conjuntos numéricos e funções matemáticas. Apresenta os conjuntos dos números naturais, inteiros, racionais e reais, além de exemplos de funções como identidade, constante, linear, afim e quadrática. Explica também o plano cartesiano e como representar graficamente diferentes tipos de funções.




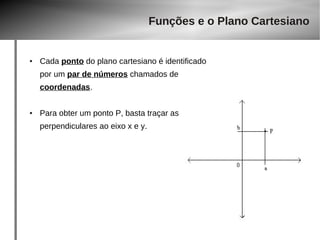
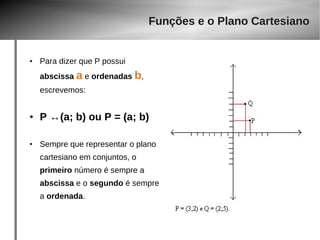

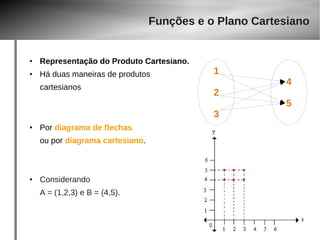
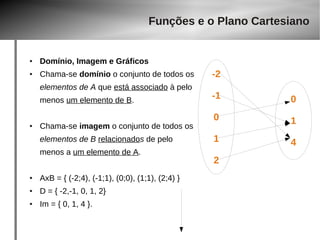




![Funções e o Plano Cartesiano
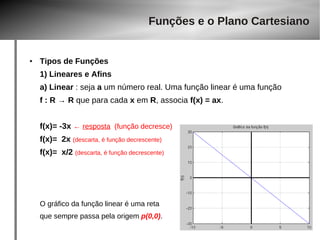
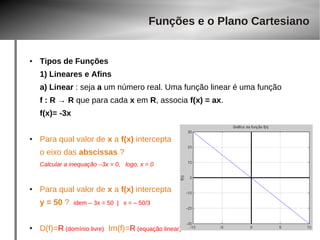
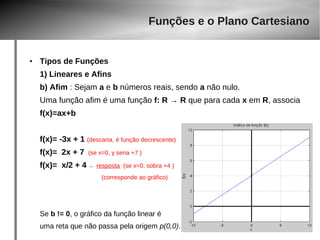
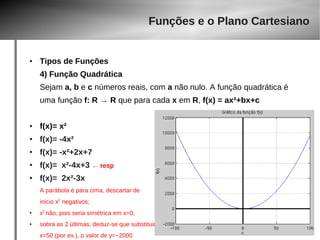
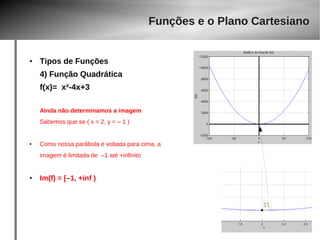
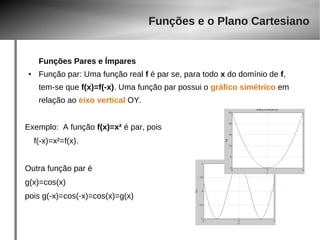
4) Função Quadrática
f(x) = x2 – 3x, somente em [-10, 40)
D(f)= [ –10, 40 ) domínio é limitado
Vy = ( 1.5, –2.25 )
Im(f)=[ –2.25, ? ] idem anterior para o
vértice, mas a imagem vai até quanto ?
Observar que temos 2 limites, [ – 10 e 40 )
Para o lado negativo, o valor máximo de y é 130 (substituindo x= –10 na função)
Para o lado positivo, o valor máximo de y é menor que 1.480 (substituindo x= 40 na função)
● Pois o intervalo é aberto em 40. Mesmo que x=39.9999999, jamais o valor de y = 1480
logo, Im(f)=[ –2.25, 1480 )](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-27-320.jpg)




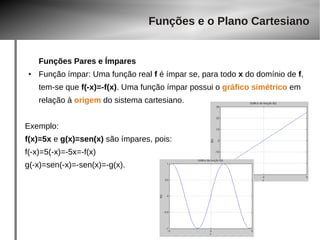
![Funções e o Plano Cartesiano
Delimitando o domínio e Imagem de uma função
● Cada função abaixo, tem características distintas
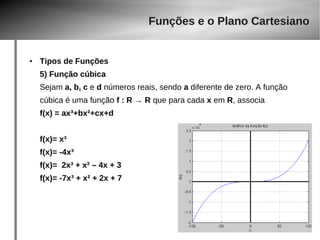
● 1) f : R → R definida por f(x)=x²
Dom(f)=R Im(f)= [ 0, +inf )
● 2) f : [0, 2] → R definida por f(x)=x²
Dom(f)=[0,2] Im(f)=[ 0,4 ]
● 3) A função modular é definida por f : R → R tal que f(x)= |x|
Dom(f)=R Im(f)= +inf
e seu gráfico ?](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-33-320.jpg)

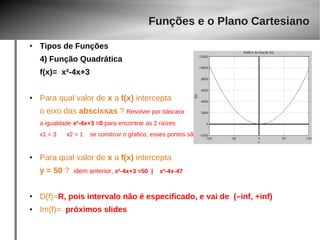
![Exercícios
Determine o gráfico da função, D(f), Im(f) para as funções dadas
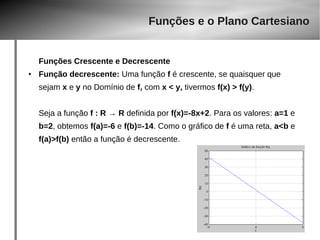
1) Uma semi-circunferência é dada pela função real f : R → R:
● Resolvendo por báscara, encontra-se as
raízes -2 e 2 (conforme gráfico)
● Qualquer valor menor que -2 ou maior que
2, faria com que a equação tivesse raízes
negativas.
● Logo, D(f) = [–2, 2]
● Imagem idem anteriores, calculando por Vy, encontramos x=0, e y=2, conforme gráfico.
Im(f) = [2, .....] como a parábola tende à –inf, se não tivéssemos o problema de raízes negativas
essa seria a resposta – Im(f) = [2, –inf ]
● Mas, como o intervalo vai somente de -2 a 2, aplica-se x=-2 e x=2 à função, para encontrar o
valor da imagem, que é 0 para qualquer uma das 2 raízes
● Logo, Im(f) = [2, 0] ou Im(f) = [0, 2]
Funções e o Plano Cartesiano
f x=4−x2](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-35-320.jpg)
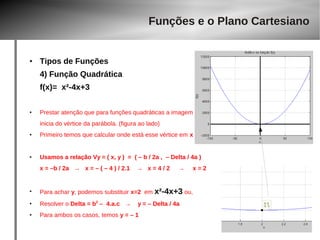
![Exercícios
Funções e o Plano Cartesiano
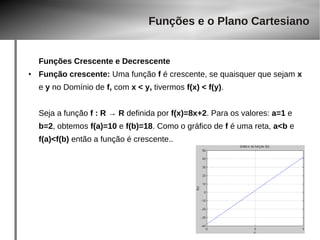
Determine o gráfico da função, D(f), Im(f) para as funções dadas
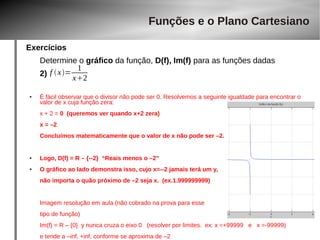
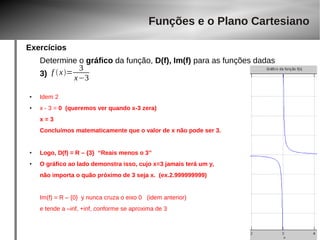
6)
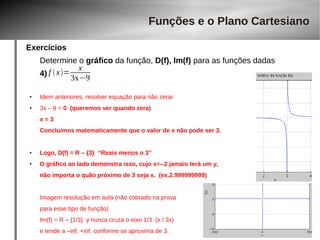
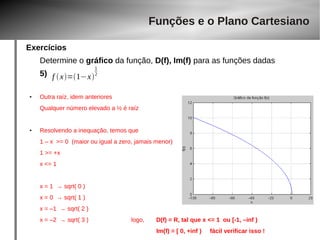
f x= 3x2
2x6−3x15
● Obviamente, aqui temos 2 situações:
– as 2 raízes não podem ser negativas ao analisadas individualmente
– o divisor não pode ser igual a zero
● Resolvendo 2x + 6 >= 0 temos x >= –3
● Resolvendo –3x + 15 >= 0 temos x <= 5 (cuidado com os sinais, que invertem as inequações)
● Logo, temos um intervalo aqui:
– situação 1 : x >= –3
– situação 2 : x <= 5
– A intersecção disso é um intervalo em [–3, 5]
● Qualquer valor fora disso torna uma das raízes negativas.... !!!!!!! aí está o domínio !
● D = [–3, 5] prove isso em { -10 -4 -3 -2 0 2 3 4 5 6 }
● Descartamos que o divisor seja 0, o que nunca ocorre dentro desse intervalo !!!!](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-40-320.jpg)
![Exercícios
Determine o gráfico da função, D(f), Im(f) para as funções dadas
6)
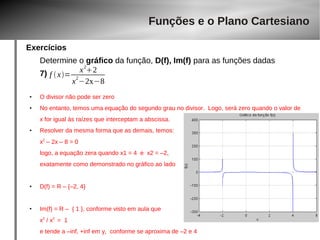
● Desenhando o gráfico da função neste intervalo, vemos que ela é contínua.
● Logo, podemos determinar a imagem aplicando
o limite negativo e o positivo na função:
● x=–3 teremos y=–1.429
● x= 5 teremos y=4.25
● Logo, Im(f) = [–1.429, 4.25 ]
● Fácil, fácil !!!!
Funções e o Plano Cartesiano
f x= 3x2
2x6−3x15](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-41-320.jpg)




![Funções e o Plano Cartesiano
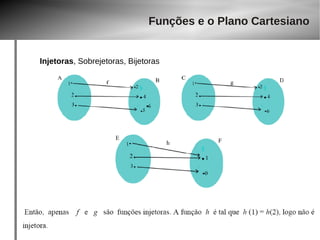
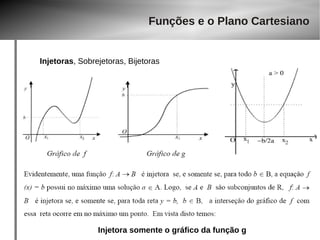
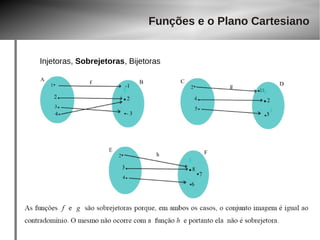
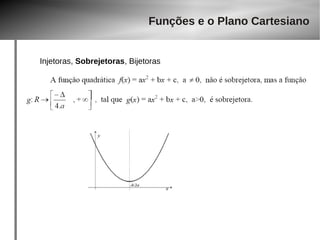
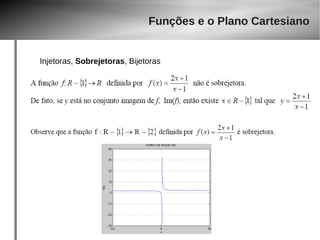
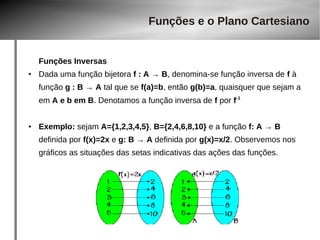
Injetoras, Sobrejetoras, Bijetoras
● Uma função f : A → B é bijetora se ela é ao mesmo tempo injetora e
sobrejetora.
● Exemplo 1: A função f : R → R dada por f(x)=2x é bijetora, pois é
injetora e sobrejetora.
● Exemplo 2: A função g : [0,+inf] → [0,+inf] dada por g(x)=x2 é bijetora
pois para que tenhamos g(x) = y
basta que tenhamos x2 = y, logo x = y1/2](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-52-320.jpg)
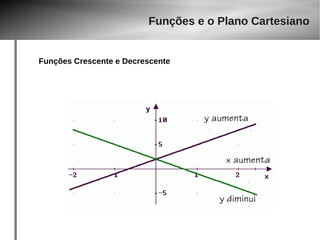
![Funções e o Plano Cartesiano
Funções Explícitas, Implícitas e Paramétricas
A função pode ser escrita de três formas diferentes:
● Paramétrica (parametrizável)
r = [x(t) y(t)], ou seja
x=x(t) e y=y(t), onde t é um parâmetro variável t1< t < t2
● Exemplo:
Uma reta:
● r(t)=(1-t)r(0) + r(1); onde r(0) é a posição inicial do segmento dos
segmento e r(1)= posição final do segmento de reta
● Uma curva qualquer
● r(t)=[t^3-0.5*t^2+1 -0.2*t^3-0.4*t^2+t ]](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-58-320.jpg)
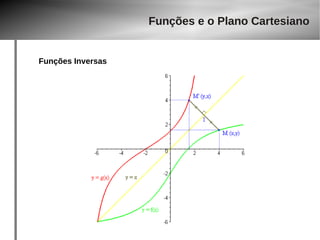

![Funções Inversas
● f(x) = 4x-5 (linha azul)
Funções e o Plano Cartesiano
● g(x) = (y+5) / 4 (linha verde)
● [0, 5]
● f(x) = x2 (linha azul)
● g(x) = x1/2 (linha verde)](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-62-320.jpg)

![Funções e o Plano Cartesiano
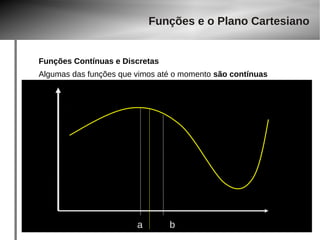
Funções Contínuas e Discretas
Outras das funções que vimos até o momento não são contínuas
a b
x in R, [0, 10]
f(x) = x – 1
x in R, x > 12
f(x) = 12](https://image.slidesharecdn.com/aula-gaba-140923143929-phpapp02/85/Aula-gaba-65-320.jpg)
