Funções Elementares

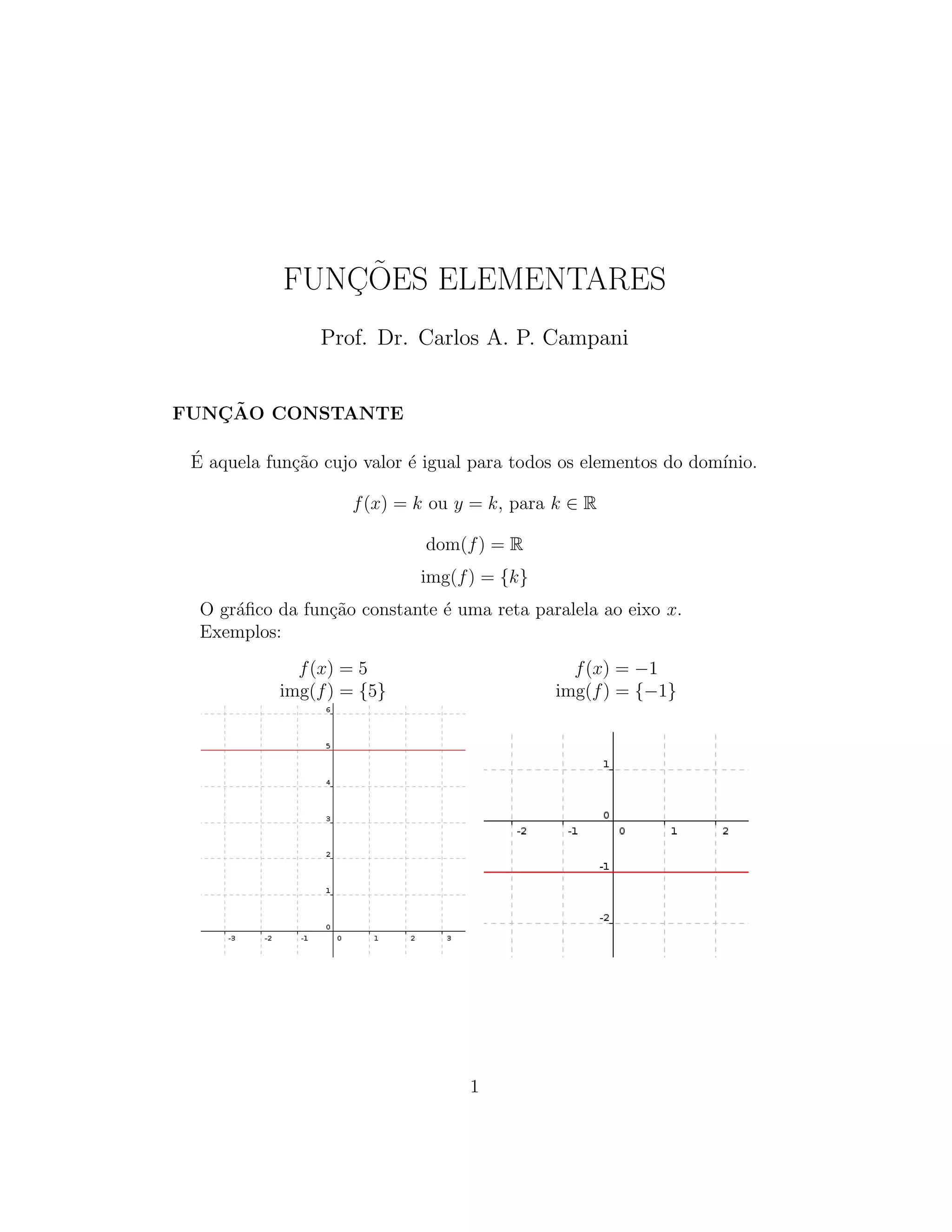
FUNÇ ÕES ELEMENTARES
Prof. Dr. Carlos A. P. Campani
FUNÇ ÃO CONSTANTE
É aquela fun¸cão cujo valor é igual para todos os elementos do dom´ınio.
f(x) = k ou y = k, para k ∈ R
dom(f) = R
img(f) = {k}
O gráfico da fun¸cão constante é uma reta paralela ao eixo x.
Exemplos:
f(x) = 5 f(x) = −1
img(f) = {5} img(f) = {−1}
1

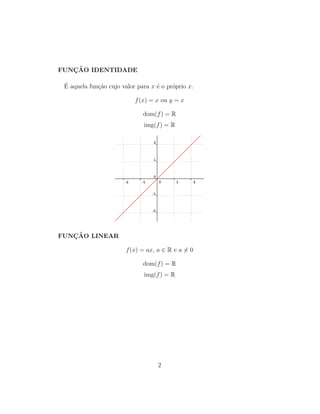
FUNÇ ÃO IDENTIDADE
É aquela fun¸cão cujo valor para x é o próprio x.
f(x) = x ou y = x
dom(f) = R
img(f) = R
FUNÇ ÃO LINEAR
f(x) = ax, a ∈ R e a = 0
dom(f) = R
img(f) = R
2

Exemplo: f(x) = 2x
FUNÇ ÃO DO 1o
GRAU OU AFIM
f(x) = ax + b com a, b ∈ R e a = 0
dom(f) = R e img(f) = R
Nesta fun¸cão, a é o coeficiente angular e b é o coeficiente linear. O coeficiente
angular é o responsável pela inclina¸cão da reta do gráfico da fun¸cão do 1o
grau. O coeficiente linear indica o ponto onde a reta intercepta o eixo y.
• a > 0: a fun¸cão é crescente
• a < 0: a fun¸cão é decrescente
3

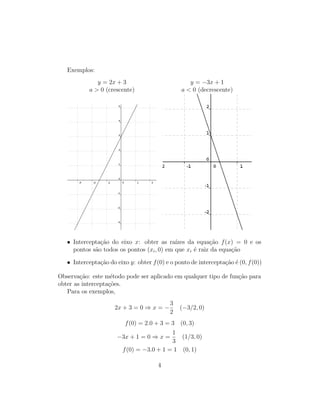
Exemplos:
y = 2x + 3 y = −3x + 1
a > 0 (crescente) a < 0 (decrescente)
• Intercepta¸cão do eixo x: obter as ra´ızes da equa¸cão f(x) = 0 e os
pontos são todos os pontos (xi, 0) em que xi é raiz da equa¸cão
• Intercepta¸cão do eixo y: obter f(0) e o ponto de intercepta¸cão é (0, f(0))
Observa¸cão: este método pode ser aplicado em qualquer tipo de fun¸cão para
obter as intercepta¸cões.
Para os exemplos,
2x + 3 = 0 ⇒ x = −
3
2
(−3/2, 0)
f(0) = 2.0 + 3 = 3 (0, 3)
−3x + 1 = 0 ⇒ x =
1
3
(1/3, 0)
f(0) = −3.0 + 1 = 1 (0, 1)
4

FUNÇ ÕES CRESCENTES E DECRESCENTES
Uma fun¸cão f : A → B, definida como y = f(x), é crescente se, para todo
x1, x2 ∈ dom(f), x1 < x2 → f(x1) < f(x2).
Ou seja, a inclina¸cão m é positiva:
m =
f(x2) − f(x1)
x2 − x1
> 0
Uma fun¸cão f : A → B, definida como y = f(x), é decrescente se, para
todo x1, x2 ∈ dom(f), x1 < x2 → f(x1) > f(x2).
Ou seja, a inclina¸cão m é negativa:
m =
f(x2) − f(x1)
x2 − x1
< 0
INCLINAÇ ÃO E SINAL DA FUNÇ ÃO DO 1o
GRAU OU AFIM
Na fun¸cão do 1o
grau, f(x) = ax + b, a inclina¸cão da reta é o coeficiente
angular a:
m =
f(x2) − f(x1)
x2 − x1
=
ax2 + b − (ax1 + b)
x2 − x1
=
ax2 + b − ax1 − b
x2 − x1
=
=
ax2 − ax1
x2 − x1
=
a(x2 − x1)
x2 − x1
= a
Consideremos a fun¸cão f(x) = ax + b, cuja raiz é ax + b = 0, x = −b/a.
Este é o valor em que a fun¸cão troca de sinal. Se a > 0, a fun¸cão é crescente
e os valores da fun¸cão para x < −b/a são negativos e os para x > −b/a
são positivos. Se a < 0, a fun¸cão é decrescente e os valores da fun¸cão para
x < −b/a são positivos e os para x > −b/a são negativos.
FUNÇ ÃO MÓDULO OU VALOR ABSOLUTO
A fun¸cão módulo ou valor absoluto,
f(x) = |x|
5

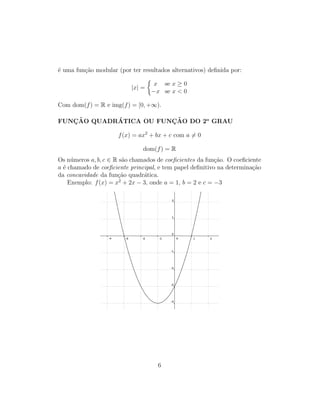
é uma fun¸cão modular (por ter resultados alternativos) definida por:
|x| =
x se x ≥ 0
−x se x < 0
Com dom(f) = R e img(f) = [0, +∞).
FUNÇ ÃO QUADRÁTICA OU FUNÇ ÃO DO 2o
GRAU
f(x) = ax2
+ bx + c com a = 0
dom(f) = R
Os números a, b, c ∈ R são chamados de coeficientes da fun¸cão. O coeficiente
a é chamado de coeficiente principal, e tem papel definitivo na determina¸cão
da concavidade da fun¸cão quadrática.
Exemplo: f(x) = x2
+ 2x − 3, onde a = 1, b = 2 e c = −3
6

GRÁFICO DA FUNÇ ÃO QUADRÁTICA
Os elementos que devem ser considerados para a determina¸cão do gráfico
da fun¸cão f(x) = ax2
+ bc + c são os seguintes:
• A curva da fun¸cão é uma parábola com eixo de simetria paralelo ao
eixo y
• A interse¸cão do eixo de simetria com a curva da parábola é um ponto
chamado de vértice
• A intercepta¸cão da curva do gráfico ao eixo y ocorre em (0, f(0)), ou
seja, em (0, c)
• Se a > 0 a parábola tem concavidade voltada para cima
• Se a < 0 a parábola tem concavidade voltada para baixo
7

Exemplos:
y = x2
+ 2x − 3 y = −2x2
+ 5x + 1
a = 1 > 0 a = −2 < 0
• A intercepta¸cão da curva do gráfico ao eixo x ocorre nos zeros da
fun¸cão, que são as ra´ızes da equa¸cão a2
+ bx + c = 0, e os valores
são dados pela fórmula de Baskara:
x =
−b ±
√
∆
2a
∆ = b2
− 4ac
Neste caso ocorrem três possibilidades:
1. ∆ > 0: duas ra´ızes reais distintas (intercepta o eixo x em dois
pontos distintos)
2. ∆ = 0: ra´ızes idênticas (intercepta o eixo x em um único ponto)
3. ∆ < 0: não há ra´ızes reais pois
√
∆ ∈ R se ∆ < 0 (não intercepta
o eixo x)
8

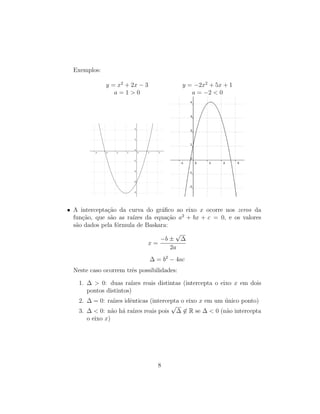
Toda fun¸cão quadrática expressa na forma canônica y = ax2
+ bx + c,
a = 0, pode ser reescrita na seguinte forma canônica:
y = a(x − xv)2
+ yv
sendo
(xv, yv) = −
b
2a
, −
∆
4a
as coordenadas do vértice da parábola, e o eixo de simetria é dado por x = xv.
Exemplo: Seja a fun¸cão y = x2
− 6x + 5.
• y = (x2
− 6x) + 5 [prop. associativa]
• y = (x2
− 6x + 9) − 9 + 5 [completa¸cão de quadrados]
• y = (x − 3)2
− 4 [produto notável e simplifica¸cão]
Neste caso, xv = 3, yv = −4, e o eixo de simetria é x = 3.
CONSTRUINDO O GRÁFICO DA FUNÇ ÃO QUADRÁTICA
Para determinar o gráfico da fun¸cão quadrática devemos considerar:
• concavidade
• vértice
• eixo de simetria
• ra´ızes
Exemplo: Seja y = 2x2
+ 4x − 1.
Como a = 2 > 0, a concavidade é voltada para cima.
As coordenadas do vértice são:
(xv, yv) = −
4
2.2
, −
24
4.2
= (−1, −3)
Eixo de simetria é x = xv = −1.
As ra´ızes são x =
−4+
√
42−4.2.(−1)
2.2
≈ 0, 2247 e x =
−4−
√
42−4.2.(−1)
2.2
≈
−2, 2247.
9

IMAGEM DA FUNÇ ÃO QUADRÁTICA
Temos dois casos:
1. a < 0: como a concavidade é voltada para baixo, o vértice é o maior
valor da fun¸cão, o que determina que img(f) = (−∞, − ∆
4a
]
2. a > 0: como a concavidade é voltada para cima, o vértice é o menor
valor da fun¸cão, o que implica que img(f) = [− ∆
4a
, +∞)
FUNÇ ÃO POLINOMIAL
A fun¸cão polinomial é definida como:
f(x) = a0xn
+ a1xn−1
+ a2xn−2
+ · · · + an−1x + an
onde n é chamado de grau da fun¸cão, a0, a1, . . . , an ∈ R são chamados de
coeficientes e a0 = 0. O dom´ınio da fun¸cão polinomial é R, dom(f) = R.
10

Exemplos:
1. f(x) = k, com k ∈ R (fun¸cão constante) - fun¸cão polinomial de grau
zero (n = 0)
2. f(x) = ax + b, com a, b ∈ R (fun¸cão afim) - fun¸cão polinomial do 1o
grau (n = 1)
3. f(x) = ax2
+ bx + c, com a, b, c ∈ R (fun¸cão quadrática) - fun¸cão
polinomial do 2o
grau (n = 2)
4. f(x) = 2x5
− 3x2
+ 5 - fun¸cão polinomial do 5o
grau (n = 5)
FUNÇ ÃO RACIONAL
A fun¸cão racional é definida como a razão
f(x) =
p(x)
q(x)
onde p(x) e q(x) são polinômios em x e q(x) = 0.
dom(f) = {x ∈ R|q(x) = 0}
Exemplos:
a) f(x) = x−1
x+1
, com dom(f) = R − {−1}
b) f(x) = 2x
x2−9
, com dom(f) = R − {−3, 3} pois −3 e 3 são ra´ızes do
polinômio do denominador
CONSTRUÇ ÃO E ANÁLISE DO GRÁFICO DA FUNÇ ÃO DO
EXEMPLO
Seja f(x) = x−1
x+1
. Já sabemos que dom(f) = R − {−1}, pois x + 1 = 0 tem
como raiz x = −1.
A fun¸cão f intercepta o eixo y em (0, −1) pois f(0) = 0−1
0+1
= −1, e
intercepta o eixo x nas ra´ızes da equa¸cão f(x) = 0, cuja solu¸cão é a raiz do
numerador, x − 1 = 0, que é x = 1. Conclui-se que a fun¸cão intercepta o
eixo x em apenas um ponto, o ponto (1, 0).
11

ASSÍNTOTAS
Como a fun¸cão não está definida em x = −1, devemos estudar o compor-
tamento da fun¸cão nas vizinhan¸cas de x = −1.
“Vizinhan¸ca” aqui denota os números que estão muito próximos do nú-
mero −1, tanto à esquerda, ou seja, para os números menores que −1, quanto
à direita, ou seja, para os números maiores que −1. Devemos observar que
os números da vizinhan¸ca, por mais próximos que estejam de −1, jamais po-
dem assumir este valor. Podemos entender a vizinhan¸ca como um caminhar
ilimitado, sobre a reta R, em dire¸cão ao número −1, pela esquerda ou pela
direita, sem jamais lá chegar.
• Caminhando pela esquerda em dire¸cão ao número −1 (por valores me-
nores que −1): −2, −1, 5, −1, 1, −1, 01, −1, 001, . . . Chamamos isso de
aproxima¸cão pela esquerda.
• Caminhando pela direita em dire¸cão ao número −1 (por valores maio-
res que −1): −0, 5, −0, 9, −0, 99, −0, 999, . . . Chamamos isso de apro-
xima¸cão pela direita.
A seguinte tabela mostra os valores da fun¸cão para a aproxima¸cão pela
esquerda, para a fun¸cão dada:
x f(x)
−1, 1 −1,1−1
−1,1+1
= 21
−1, 01 −1,01−1
−1,01+1
= 201
−1, 001 −1,001−1
−1,001+1
= 2001
−1, 0001 −1,0001−1
−1,0001+1
= 20001
...
...
Ou seja, quanto mais próximo de −1 pela esquerda, maior o valor da
fun¸cão em valor absoluto, com sinal positivo.
12

Isso pode ser expresso usando a nota¸cão de limites:
x → −1−
⇒ f(x) → +∞
Isso pode ser lido como:“quando x se aproxima de −1 pela esquerda, isso
implica que f(x) tende para +∞”.
Ou então, podemos usar a seguinte nota¸cão:
lim
x→−1−
f(x) = +∞
Isso pode ser lido como: “o limite de f(x) quando x se aproxima de (ou
tende para) −1 pela esquerda é +∞”.
A seguinte tabela mostra os valores da fun¸cão para a aproxima¸cão pela
direita, para a fun¸cão dada:
x f(x)
−0, 9 −0,9−1
−0,9+1
= −19
−0, 99 −0,99−1
−0,99+1
= −199
−0, 999 −0,999−1
−0,999+1
= −1999
−0, 9999 −0,9999−1
−0,9999+1
= −19999
...
...
Ou seja, quanto mais próximo de −1 pela direita, maior o valor da fun¸cão
em valor absoluto, com sinal negativo.
Isso pode ser expresso usando a nota¸cão de limites:
x → −1+
⇒ f(x) → −∞
Isso pode ser lido como:“quando x se aproxima de −1 pela direita, isso
implica que f(x) tende para −∞”.
lim
x→−1+
f(x) = −∞
Isso pode ser lido como: “o limite de f(x) quando x se aproxima de (ou
tende para) −1 pela direita é −∞”.
13

No gráfico da fun¸cão, estes dois limites serão percebidos como a curva da
fun¸cão tangenciando a reta vertical x = −1, indo para +∞ no lado esquerdo
e para −∞ do lado direito da reta, como mostra a figura:
O número −1 é uma descontinuidade infinita, pelo valor da fun¸cão no
ponto estar indefinido e nas proximidades do ponto a fun¸cão assumir valor
infinito. A reta vertical x = −1 é chamada de ass´ıntota vertical da fun¸cão.
Isso conclui o que chamamos de análise de ass´ıntotas verticais.
Agora, precisamos analisar o que ocorre com a fun¸cão para valores muito
grandes, tanto positivos quanto negativos. Ou seja, precisamos fazer a análise
do comportamento da fun¸cão nos extremos do eixo x.
14

Vamos come¸car analisando os valores da fun¸cão quando x cresce ilimita-
damente para valores positivos. A seguinte tabela mostra os valores que a
fun¸cão dada assume quando x cresce para +∞:
x f(x)
10 10−1
10+1
≈ 0, 8181
100 100−1
100+1
≈ 0, 9801
1000 1000−1
1000+1
≈ 0, 998
10000 10000−1
10000+1
≈ 0, 9998
...
...
Isso sugere que o valor da fun¸cão se aproxima de 1, por valores menores
que 1. Podemos usar a seguinte nota¸cão para expressar isso:
x → +∞ ⇒ f(x) → 1−
Isso pode ser lido como: “quando x tende para +∞, o valor de f(x) se
aproxima de 1 por baixo”.
lim
x→+∞
f(x) = 1−
Isso pode ser lido como: “o limite de f(x) quando x tende para +∞ é
igual a 1, com f(x) aproximando-se de 1 por baixo”.
Agora fazemos a mesma coisa para x tendendo para −∞:
x f(x)
−10 −10−1
−10+1
≈ 1, 2222
−100 −100−1
−100+1
≈ 1, 0202
−1000 −1000−1
−1000+1
≈ 1, 0020
−10000 −10000−1
−10000+1
≈ 1, 0002
...
...
15

Isso significa que o valor da fun¸cão se aproxima de 1, por valores maiores
que 1. Podemos usar a seguinte nota¸cão para expressar isso:
x → −∞ ⇒ f(x) → 1+
Isso pode ser lido como: “quando x tende para −∞, o valor de f(x) se
aproxima de 1 por cima”.
lim
x→−∞
f(x) = 1+
Isso pode ser lido como: “o limite de f(x) quando x tende para −∞ é
igual a 1, com f(x) aproximando-se de 1 por cima”.
No gráfico da fun¸cão, estes dois limites, x → +∞ e x → −∞, serão
percebidos como a curva da fun¸cão tangenciando a reta horizontal y = 1,
aproximando-se o valor da fun¸cão de 1, por cima e por baixo, como mostra
a figura:
A reta horizontal y = 1 é chamada de ass´ıntota horizontal da fun¸cão.
E isso completa a análise do comportamento da fun¸cão nos extremos do
eixo x.
16

ARTICULANDO TODOS OS RESULTADOS NO GRÁFICO
Sobre a fun¸cão f(x) = x−1
x+1
sabemos que ela possui uma indetermina¸cão
infinita em x = −1, onde ocorre uma ass´ıntota vertical, que cruza o eixo x
em x = 1 e o eixo y em y = −1. Além disto, sabemos que ela possui uma
ass´ıntota horizontal em y = 1. Combinando todas as informa¸cões podemos
obter facilmente o gráfico completo da fun¸cão, apresentado na imagem acima.
17

Funções Elementares

Mais conteúdo relacionado

Mais procurados

Semelhante a Funções Elementares

Mais de Carlos Campani

Funções Elementares