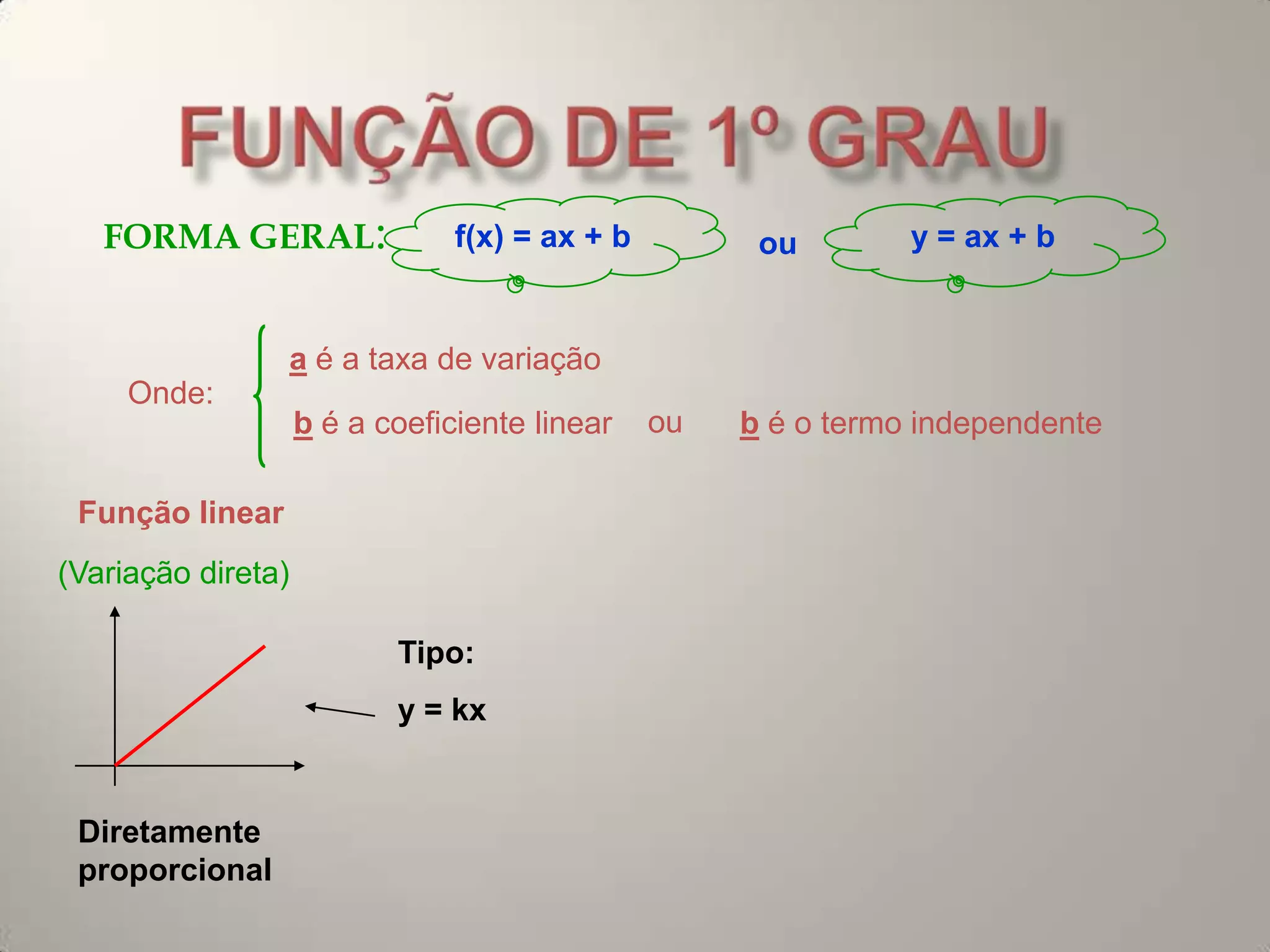
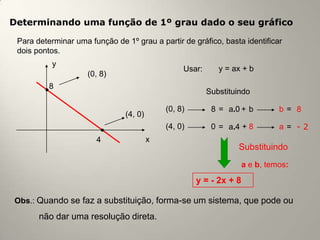
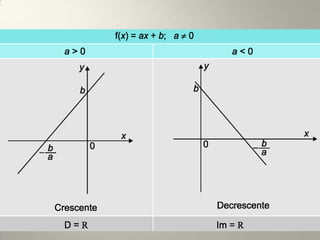
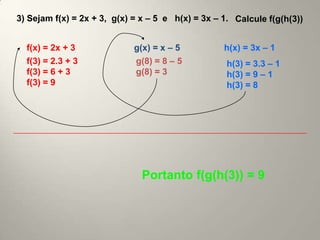
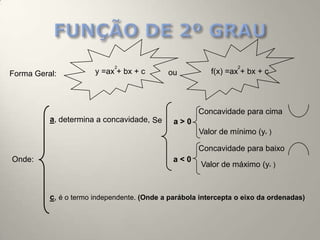
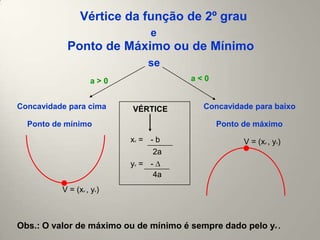
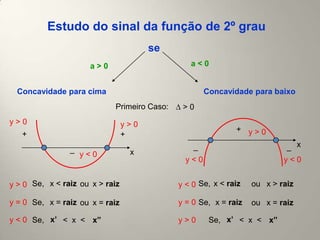
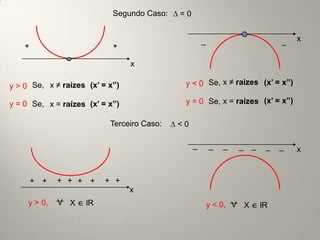
Este documento resume os principais conceitos de funções do 1o e 2o grau. No 1o grau, explica a forma geral da função linear f(x)=ax+b e conceitos como crescimento, decrescimento, raiz e estudo do sinal. No 2o grau, aborda a forma geral da parábola f(x)=ax2+bx+c, conceitos como vértice, concavidade, raízes e estudo do sinal.

1. FORMA GERAL: f(x) = ax + b ou y = ax + b
a é a taxa de variação
Onde:
b é a coeficiente linear ou b é o termo independente
Função linear
(Variação direta)
Tipo:
y = kx
Diretamente
proporcional

2. Função afim ou função linear
y = ax + b
a>0 Função crescente
Crescimento ou decrescimento: se
a<0 Função decrescente
ALGEBRICAMENTE
É o valor de x que torna y igual a zero
Zero ou Raiz de uma função:
GEOMETRICAMENTE (GRAFICAMENTE)
É a interseção da reta com o eixo x

3. RAIZ (OU ZERO) DA FUNÇÃO
Dada a função de f: lR lR, definida: f(x) = 2x + 8, Calcule o zero da função:
Igualar a função a zero 2x + 8 = 0
Fazer os cálculos 2x = - 8
Determinado o valor de x x = -4
Geometricamente teremos o ponto: (- 4, 0)
-4 x

4. Estudo do sinal de uma função
se
a>0 a<0
Função crescente Função decrescente
(y > 0) (y > 0)
+ +
x x
(y < 0) - raiz raiz -
(y < 0)
y > 0 se x > ......(raiz) y > 0 se x < ......(raiz)
y = 0 se x = ......(raiz) y = 0 se x = ......(raiz)
y < 0 se x < ......(raiz) y < 0 se x > ......(raiz)

5. Determinando uma função de 1º grau dado o seu gráfico
Para determinar uma função de 1º grau a partir de gráfico, basta identificar
dois pontos.
y
Usar: y = ax + b
(0, 8)
8
Substituindo
(0, 8) 8 = a.0 + b b= 8
(4, 0)
(4, 0) 0 = a.4 + 8 a= -2
4 x
Substituindo
a e b, temos:
y = - 2x + 8
Obs.: Quando se faz a substituição, forma-se um sistema, que pode ou
não dar uma resolução direta.

8. NOTAÇÕES f(x) = 2x + 1
f(…) = 2(…) + 1
f(g(x)) = fog (x)
g(f(x)) = gof (x) f(g(x)) = 2g(x) + 1
f(f(x)) = fof(x) f(g(x)) = 2(4x – 3) + 1
f(g(x)) = 8x – 6 + 1
1) Dadas as funções f(x) = 2x + 1
e g(x) = 4x – 3. Determinar
f(g(x))
f(g(x)) = 8x – 5

9. 2) Sejam f e g funções reais definidas por f(x) = x + 3, g(x) = 2x – 1.
O valor de f(g(5)) é:
1o Modo 2o Modo
Vamos obter primeiramente a f(g(x)) Vamos “abrir a função”
f(x) = x + 3 Como queremos calcular
f(g(5)) ,procedemos assim:
f(…) = (…) + 3
f(g(x)) = g(x) + 3 f(x) = x + 3 g(x) = 2x – 1
f(9) = 9 + 3 g(5) = 2.5 – 1
f(g(x)) = 2x – 1 + 3
f(9) = 12 g(5) = 10 – 1
f(g(x)) = 2x + 2 g(5) = 9
Se f(g(x)) = 2x + 2, então: Portanto f(g(5)) = 12
f(g(5)) = 2.5 + 2
f(g(5)) = 12

10. 3) Sejam f(x) = 2x + 3, g(x) = x – 5 e h(x) = 3x – 1. Calcule f(g(h(3))
f(x) = 2x + 3 g(x) = x – 5 h(x) = 3x – 1
f(3) = 2.3 + 3 g(8) = 8 – 5 h(3) = 3.3 – 1
f(3) = 6 + 3 g(8) = 3 h(3) = 9 – 1
f(3) = 9 h(3) = 8
Portanto f(g(h(3)) = 9

11. 4) ( CEFET – PR ) Sendo f(x) = x + 2 e f(g(x)) = 2x – 3, então g(x)
é igual a:
f(x) = x + 2
f(g(x)) = g(x) + 2
2x – 3 = g(x) + 2
2x – 3 – 2 = g(x)
2x – 5 = g(x)

13. 2) Encontre a inversa da função
Para encontrar a inversa de uma função,
o processo prático é trocar x por y e em 2x - 1
f(x)
seguida isolar y. x 3
3x 1
2x - 1 y=
f(x) x 2
x 3
2y 1 1 3x 1
x= f (x)
y 3 x 2
x(y – 3) = 2y – 1
1) Seja f(x) = 2x + 3. Obtenha f -1(x). xy – 3x = 2y – 1
f(x) = 2x + 3 1 x 3 xy – 2y = 3x – 1
f ( x)
x = 2y + 3 2 xy – 2y = 3x – 1
x – 3 = 2y y(x – 2) = 3x – 1
x 3
y
2

14. 3) ( UFSC ) Seja a função f(x) = 2x Determine f -1(2)
x 2
PASSO 1: determinar a inversa de f(x) PASSO 2: determinar f-1 (2)
2x 2x
f ( x)
y 2x
x 2
x 2 f (x)
1
x
2y x 2
y 2 2x
f (x)
1
2.2
x(y – 2) = – 2y x 2 1
f (2)
xy – 2x = – 2y 2 2
xy + 2y = 2x
1 4
xy + 2y = 2x f (2)
y(x + 2) = 2x 4
Portanto f-1(2) = 1

15. 2 2
Forma Geral: y =ax + bx + c ou f(x) =ax + bx + c
Concavidade para cima
a, determina a concavidade, Se a>0
Valor de mínimo (yv )
Concavidade para baixo
Onde: a<0
Valor de máximo (yv )
c, é o termo independente. (Onde a parábola intercepta o eixo da ordenadas)

16. ZEROS (OU RAÍZES) DE UMA FUNÇÃO DE 2º grau
2
Dada a função de f: lR lR, definida: f(x) = x + 3 x + 2, Calcule o zero da função:
Determinar a concavidade: Concavidade para cima
2
Igualar a função a zero x +3x+ 2 = 0
2
Fazer os cálculos = 3 - 4 .1 .2 x= -3 V1
=1 2.1
Determinado o valor de x X’ = - 2 e X’ = - 1
Geometricamente teremos os pontos: (- 1, 0) e (- 2, 0)
x
-2 -1

17. Vértice da função de 2º grau
e
Ponto de Máximo ou de Mínimo
se
a>0 a<0
Concavidade para cima VÉRTICE Concavidade para baixo
Ponto de mínimo Ponto de máximo
xv = - b V = (xv , yv)
2a
yv = -
4a
V = (xv , yv)
Obs.: O valor de máximo ou de mínimo é sempre dado pelo yv .

18. Estudo do sinal da função de 2º grau
se
a>0 a<0
Concavidade para cima Concavidade para baixo
Primeiro Caso: >0
y>0 y>0
+ y>0
+ +
_ _ _ x
y<0 x
y<0 y<0
y > 0 Se, x < raiz ou x > raiz y < 0 Se, x < raiz ou x > raiz
y = 0 Se, x = raiz ou x = raiz y = 0 Se, x = raiz ou x = raiz
y < 0 Se, x’ < x < x” y>0 Se, x’ < x < x”

19. Segundo Caso: =0
_ _ x
+ +
x
y > 0 Se, x ≠ raízes (x’ = x”) y < 0 Se, x ≠ raízes (x’ = x”)
y = 0 Se, x = raízes (x’ = x”) y = 0 Se, x = raízes (x’ = x”)
Terceiro Caso: <0
_ _ _ _ _ _ _ x
+ + + + + + + +
x
y > 0, V X lR y < 0, V X lR