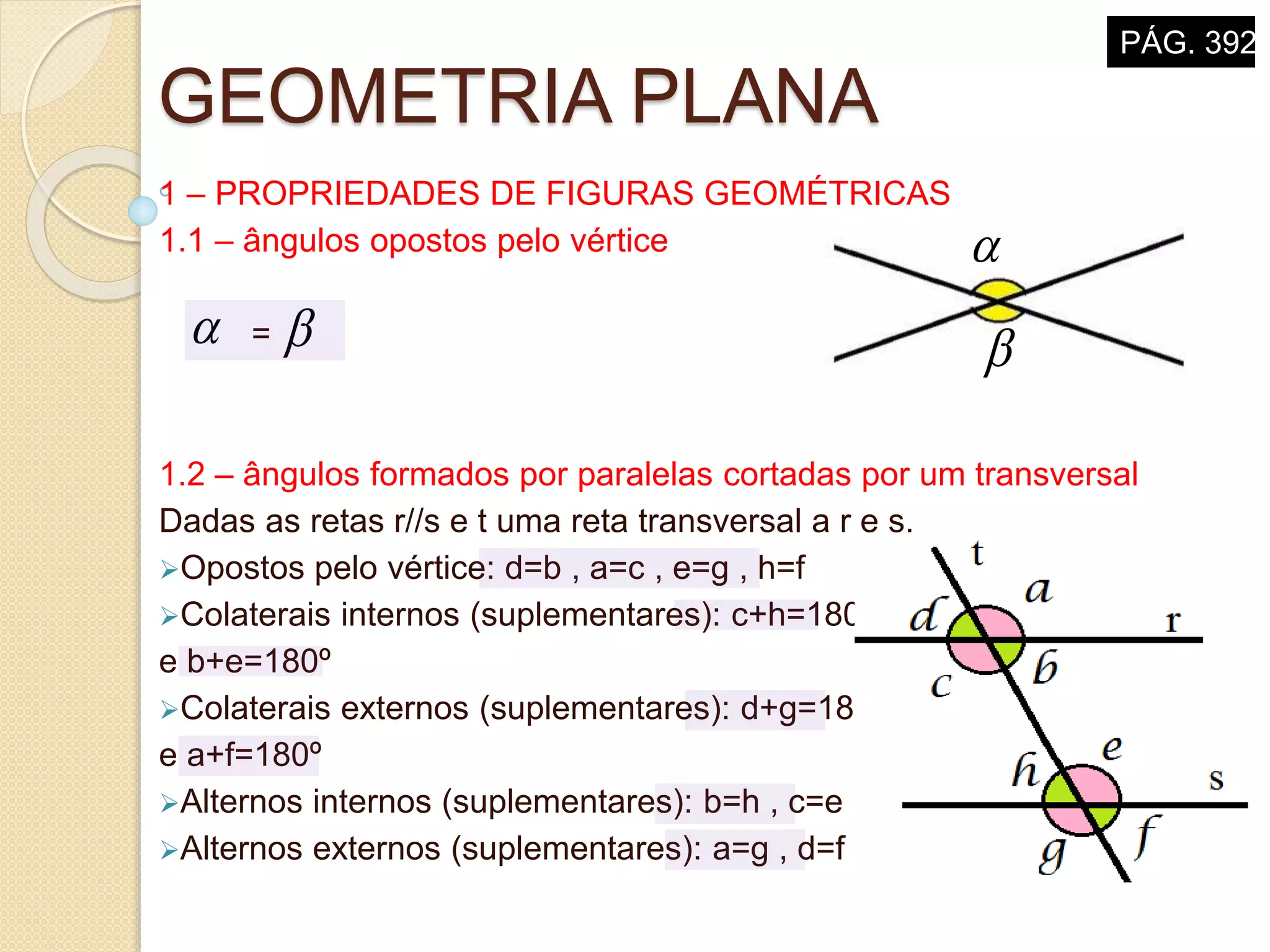
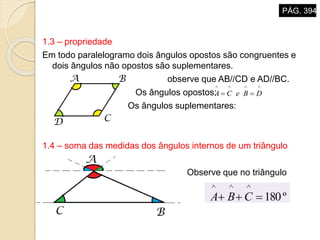
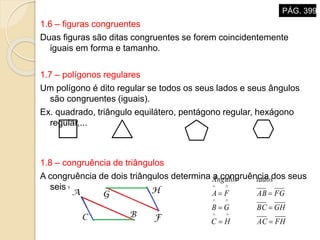
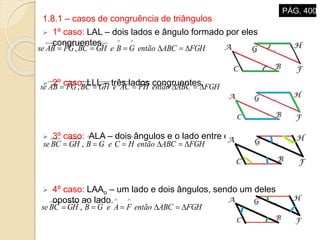
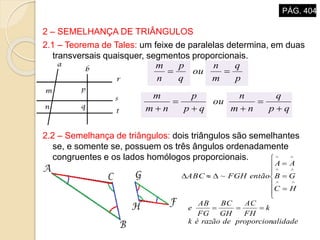
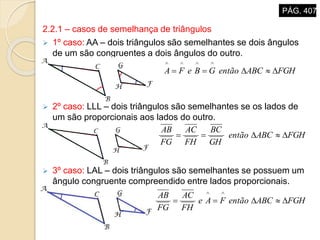
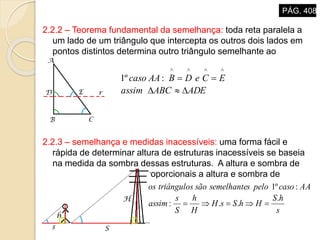
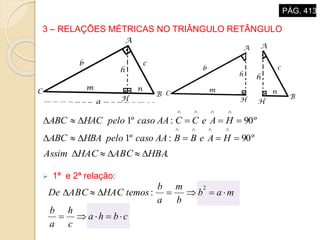
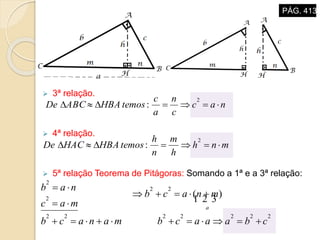
O documento descreve propriedades geométricas de figuras planas como triângulos, quadriláteros e polígonos. Inclui relações entre ângulos formados por paralelas cortadas por um transversal, soma dos ângulos internos de polígonos convexos, casos de congruência e semelhança de triângulos, e relações métricas no triângulo retângulo como o Teorema de Pitágoras.