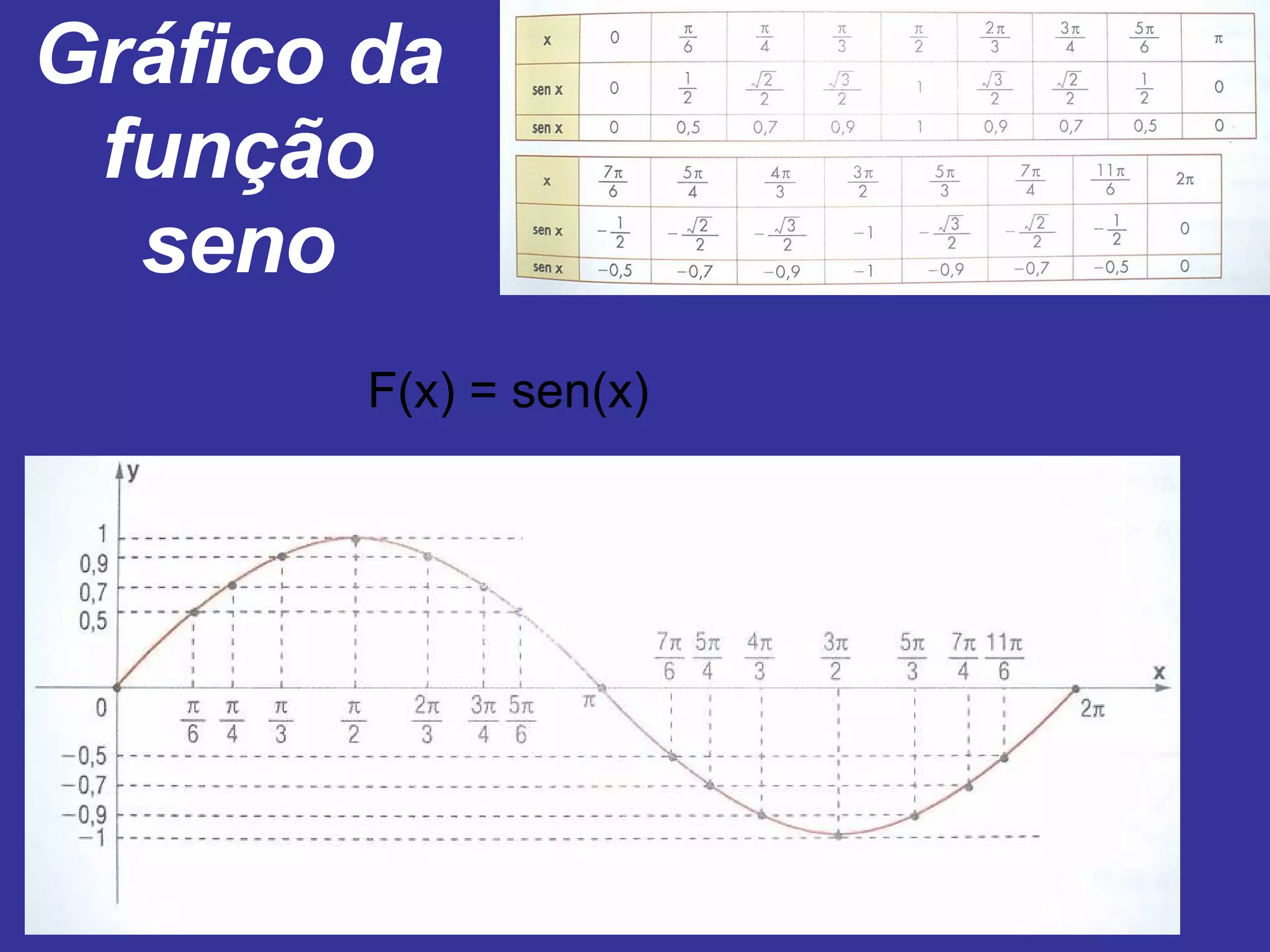
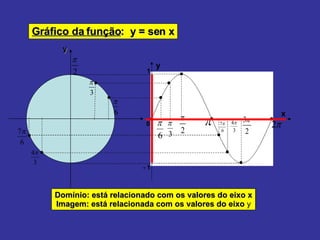
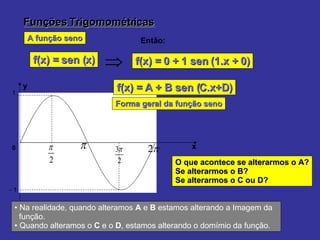
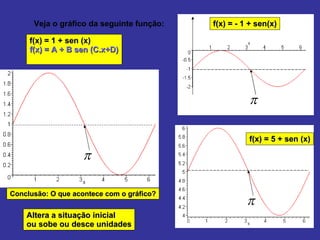
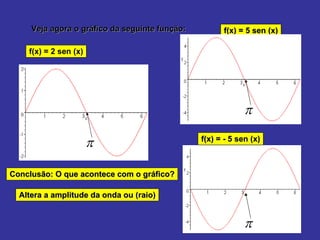
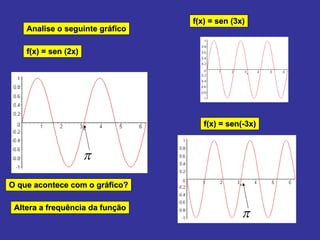
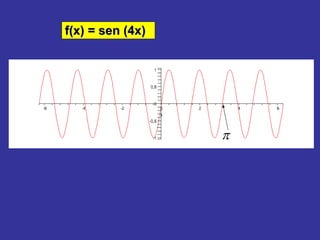
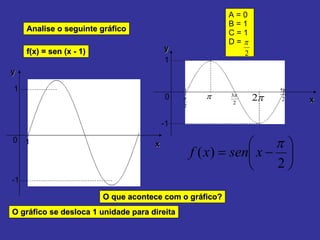
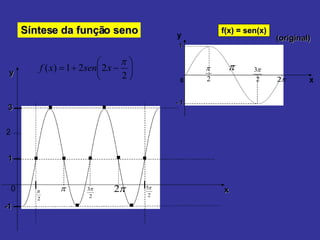
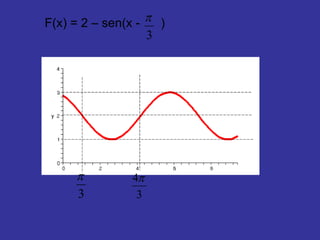
O documento explica como alterar os parâmetros A, B, C e D na função seno f(x) = A + B sen (Cx + D) afeta o gráfico. Alterar A e B muda a imagem, enquanto alterar C e D muda o domínio. Exemplos mostram como diferentes valores para esses parâmetros deslocam, estendem ou comprimem o gráfico da onda senoidal.

1. Gráfico da função seno F(x) = sen(x)

2. Gráfico da função : y = sen x Domínio: está relacionado com os valores do eixo x Imagem: está relacionada com os valores do eixo y 0 x 1 - 1 y y

3. Funções Trigomométricas A função seno f(x) = sen (x) Então: f(x) = 0 + 1 sen (1.x + 0) O que acontece se alterarmos o A? Se alterarmos o B? Se alterarmos o C ou D? Na realidade, quando alteramos A e B estamos alterando a Imagem da função. Quando alteramos o C e o D , estamos alterando o domímio da função. 0 x 1 - 1 y Forma geral da função seno f(x) = A + B sen (C.x+D)

4. Veja o gráfico da seguinte função: f(x) = 1 + sen (x) f(x) = A + B sen (C.x+D) Conclusão: O que acontece com o gráfico? Altera a situação inicial ou sobe ou desce unidades f(x) = 5 + sen (x) f(x) = - 1 + sen(x)

5. Veja agora o gráfico da seguinte função: f(x) = 2 sen (x) Conclusão: O que acontece com o gráfico? Altera a amplitude da onda ou (raio) f(x) = 5 sen (x) f(x) = - 5 sen (x)

6. Analise o seguinte gráfico f(x) = sen (2x) O que acontece com o gráfico? Altera a frequência da função f(x) = sen (3x) f(x) = sen(-3x)

7. f(x) = sen (4x)

8. Analise o seguinte gráfico f(x) = sen (x - 1) O que acontece com o gráfico? O gráfico se desloca 1 unidade para direita x y 1 0 1 -1 0 x y 1 -1 A = 0 B = 1 C = 1 D =

9. Síntese da função seno x y 0 -1 1 2 3 . . . . . . . . . f(x) = sen(x) (original) 0 x 1 - 1 y

10. F(x) = 2 – sen(x - )