1) O documento discute funções compostas e funções inversas, apresentando suas definições e exemplos de exercícios resolvidos. 2) A seção de funções compostas explica o que é uma função composta e apresenta um exercício resolvido. 3) A seção de função inversa define o que é uma função inversa e fornece a regra prática para obter a função inversa de uma função bijetora.

1. MATEMÁTICA – A1
Resolução:
Determinando as somas:
AULA 10
1
f(x) + g(x) = x 2  2x  3  x 1
2
FUNÇÃO COMPOSTA
3
f(x) + g(x) = x 2  x 4
Sejam as funções f: A  B e g: B  C, chama-se 2
função composta de g com f à função h: A  C tal que e
h(x) = g[f(x)] = g o f(x). 1
g(x) - f(x) = x  1  x 2  2x + 3
2
5
g(x) - f(x) =  x 2  x + 2
2
Analisando as proposições:
1. Falsa, pois f(x) + g(x) é uma parábola e por tanto possui
dois zeros.
2. Verdadeira, pois  a,b[2,5] se a < b tem-se h(a) < h(b)
onde h(x) = f(x) + g(x).
5
3. Verdadeira, pois sendo g(x) – f(x) =  x 2  x + 2 >0
2
para qualquer x que pertence ao intervalo (0,3).
(fog)(0) = f(g(0)) = f(-1) = 0

4. Falsa, pois  5
(gof)(0) = g(f(0)) = g(-3) = - 2

R: Alternativa a
EXERCÍCIOS DE SALA 03) (ACAFE) Dadas as funções reais f(x) = 2x - 6 e
g(x) = ax + b, se f[g(x)] = 12x + 8, o valor de a + b, é:
01) Sejam f e g duas funções reais tais que f(x) = 2x – 1 a) 10
e g(x) = x2 – 2. Então a função (fog)(x) é igual a: b) 13
a) 2x2 – 3 c) 12
b) 2x2 + 3 d) 20
2
c) 2x – 5 e) 8
d) 2x2 + 5
2
e) 2x - 1 Resolução:
Resolução  
f g  x   12x  8
(fog)(x)  f(g(x)) 2g  x   6  12x  8
(fog)(x)  f(x  2)
2
g  x   6x  7
(fog)(x)  2(x 2  2)  1 Mas,
(fog)(x)  2x 2  4  1 g  x   ax  b
(fog)(x)  2x 2  5
Então :
R: Alternativa c
a  b  13
02) (UFPR) Considere as afirmativas abaixo a respeito R: Alternativa b
1
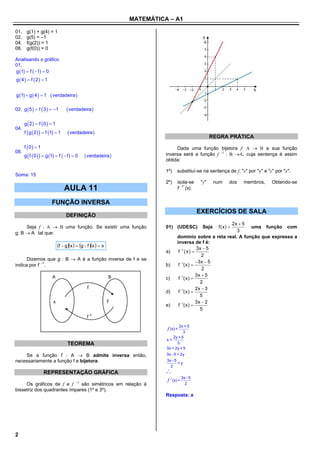
das funções f(x)  x 2  2x  3 e g(x)  x  1 , com 04) O gráfico abaixo representa a função f(x), definida
2 no intervalo [–1, 4].
x  R:
1. A função f(x) + g(x) tem exatamente três zeros.
2. A função f(x) + g(x) é crescente no intervalo [2,5].
3. A função g(x) – f(x) é positiva no intervalo aberto (0,3).
4. Quando x = 0, tem-se (fog)(x) = (gof)(x).
Assinale a alternativa correta.
a) Somente as afirmativas 2 e 3 são verdadeiras.
b) Somente as afirmativas 1 e 3 são verdadeiras.
c) Somente as afirmativas 3 e 4 são verdadeiras.
d) Somente as afirmativas 1 e 2 são verdadeiras.
e) Somente as afirmativas 2 e 4 são verdadeiras.
Considerando que g(x) = f(x–2), assinale o que for
correto.
1

2. MATEMÁTICA – A1
01. g(1) + g(4) = 1
02. g(5) = –1
04. f(g(2)) = 1
08. g(f(0)) = 0
Analisando o gráfico
01.
g 1  f  1  0
g  4   f  2  1
g 1  g  4   1  verdadeira 
02. g  5   f  3   1  verdadeira 
g  2  f 0   1
04.
f  g  2    f 1  1  verdadeira 
REGRA PRÁTICA
f 0  1 Dada uma função bijetora f: A  B a sua função
08.
g  f  0    g 1  f  1  0  verdadeira  inversa será a função f 1 : B A, cuja sentença é assim
obtida:
1º) substituí-se na sentença de f, "x" por "y" e "y" por "x".
Soma: 15
2º) isola-se "y" num dos membros, Obtendo-se
AULA 11 f 1 (x).
FUNÇÃO INVERSA
EXERCÍCIOS DE SALA
DEFINIÇÃO
2x  5
Seja f : A  B uma função. Se existir uma função 01) (UDESC) Seja f(x)  uma função com
g: B  A tal que: 3
domínio sobre a reta real. A função que expressa a
inversa de f é:
f  gx   g  f x   x 3x  5
a) f 1  x  
2
Dizemos que g : B  A é a função inversa de f e se
3x  5
indica por f 1. b) 1
f (x) 
2
3x  5
c) f 1(x) 
2
2x  3
d) f 1(x) 
5
1 3x  2
e) f (x) 
5
2x + 5
f (x) =
3
2y + 5
x=
TEOREMA 3
3x = 2y + 5
Se a função f : A  B admite inversa então, 3x - 5 = 2y
necessariamente a função f e bijetora. 3x - 5
=y
2
REPRESENTAÇÃO GRÁFICA 
3x - 5
f -1(x) =
Os gráficos de f e f 1 são simétricos em relação à 2
bissetriz dos quadrantes ímpares (1º e 3º).
Resposta: a
2

3. MATEMÁTICA – A1
02) Determine a função inversa da função 02) Considere as funções reais f e g tais que f(x) = x + 3
f : IR  IR definida por f x   2x  4 e construa os
2
e g(x) = x - 4. O valor de f 0 g(2) é:
gráficos das duas funções em um mesmo sistema a) 1
de referências. b) 2
c) 3
d) 4
e) 5
f(x)  2x  4
x  2y  4 g  2   22  4
x4
y g  2  0
2
 
f g  2   F(0)
 f 1  x  
x4 f  g  2  0  3
2
f  g  2  3
Resposta: c
03) Sejam as funções reais f e g tais que f(x) = x + 3 e
2
g(x) = x - 4. O valor da expressão [f(g(2)) + g(f(1))] é
igual a:
a) 0
b) 15
03) (UDESC) Se f : IR  {3}  IR  {a} definida por c) -15
1 d) 20
f(x)  é inversível, então, o valor de a é: e) 12
x3
a) 3
b) 5    
f g  2   g f 1  3  g 1  3 
c) –3
d) 0 f  g  2    g  f 1   3  g  4 
f  g  2    g  f 1   3   4   4
e) 2 2
f  g  2    g  f 1   15
Resolução:
1 1
f(x)  y Resposta: b
x3 x3
Trocando x por y e y por x: 04) Considere as funções reais f e g tais que f(x) = x + 3
1 e g(x) = 2x - 5. A função (g 0 f)(x) é definida como
x
y 3 sendo:
x(y  3)  1 a) x + 1
b) 2x + 3
1 1 c) x-1
y   3  f 1(x)   3
x x d) 2x + 5
Assim, x  0. e) 2x + 1
R: Alternativa d
 
g f  x   g  x  3
EXERCÍCIOS-TAREFA g  f  x    2  3   5
AULAS 10 e 11 g  f  x    2x  6  5
g  f  x    2x  1
01) Sejam as funções reais f e g tais que f(x) = x + 3 e
g(x) = x2 - 4. O valor da expressão [f(2) + g(1)] é Resposta: e
igual a:
a) 0 05) Se f(x + 1) = x2 +2, então f(3) é igual a:
b) 1 a) 2
c) -1 b) 4
d) 2 c) 6
e) -2 d) 11
e) 18
f  2   g 1  2  3  1  4
2
f  x  1  x 2  2
f  2   g 1  5  3 f  2  x   22  2
f  2   g 1  2 f 3  6
Resposta: d Resposta: c
3

4. MATEMÁTICA – A1
06) A função f: IR  IR é tal que 09) (UDESC) Considere as funções f e g de IR em IR
f(8x) = 4f(x). Se f(8) = 16, então f(1) vale: definidas por:
a) 16
b) 4  x  6, se x  0
c) 8 f x   
d) 2 2x  5, se x  0
e) 1 e

f  8x   4f  x  2x 2  5, se x  0
gx    3
x , se x  0

f  8.1  4f 1
f  8   4f 1
Calcule gf 3  .
16
 f 1 a) 8
4 b) 16
f 1  4 c) 27
d) 25
Resposta: b e) -8
07) Seja f: IR  IR uma função tal que g  3  6 
f(3x +1) = 1 – x. Então f(a) é:
a) 1 – a g 3
b) 3a + 1
c) - 3a 33
4a 27
d) Resposta: c
3
e) 4 – 3a
10) (UDESC) A função f é tal que
f(2x + 3) = 3x + 2. Nessas condições,
f(3x + 2), é igual a:
f  3x  1  1  x
9 1
y 1
a) x
f  y   1 2 2
3x  1  y 3 b) 2x  3
3  y 1
3x  y-1 f y  c)
2
x 1
3 3
y 1
x 4y 3x  2
3 f y  d)
3 e) 3x – 2
4a
f a  2x  3  y
3
Resposta: d 2x  y  3
y3
08) Se f e g são funções de IR em IR tais que x
2
f(x) = 2x - 1 e f(g(x)) = x2 - 1, então:
a) g x 
x2  2 f  2x  3   3x  2 Então:
2 3  3x  2   5
 y3 f  3x  2  
x2 f y  3  2
gx 
2
b)  2 
2 9x  6  5
3y  9 f  3x  2  
1 f y  2
g  x   x2 
2
c) 2
9x  1
f  3x  2  
2
3y  9  4
x2 f y  2
d) gx  2
3 3y  5
3x 2 f y 
e) g x  2
2 Resposta: a
 
f g  x   x2  1 11) Uma função f de variável real satisfaz à condição
f(x + 1) = f(x) + f(1), qualquer que seja o valor da
2g  x   1  x 2  1 variável x. Sabendo que f(2) = 1, podemos concluir
que f(5) é igual a:
x2
gx  a)
1
2 2
Alternativa b b) 1
5
c)
2
d) 5
e) 10
4

5. MATEMÁTICA – A1
f(x +1) = f(x) + f(1) 14) Os gráficos das funções reais definidas por
f(x) = x – 1 e g(x)= k , 1  k > 0, se interceptam num
2 x
1
x = 1  f(2) = 2f(1)  f(1)  ponto de abscissa 3. O valor de f(g(k)) é:
2
g  x   k2
1
x  2  f(3)  f(2)  f(1)   1 
3
f  g  P  3, y     
f g  2   f 22
2 2 g 3  k3
3 1 f  3   32  1 f  g  2   f  4 
x  3  f(4)  f(3)  f(1)    2 8  k3
2 2 f 3  8 f  g  2    42  1
1 5 23  k 3
x  4  f(5)  f(4)  f(1)  2   P  3,8  f  g  2    15
2 2 k2
R: Alternativa C.
15) Os valores positivos de a e b, sabendo que
12) (UFSC) Seja f uma função polinomial do primeiro
(ff) (x) = x + 1 e que f(x) = ax +b são
grau, decrescente, tal que f(3) = 2 e f(f(1)) = 1.
respectivamente:
Determine a abscissa do ponto onde o gráfico de f
a) 1 e 2
corta o eixo x.
b) 3 e 4
c) 2e2
Resolução:
d) 1 e 3
Se a função f é de primeiro grau e decrescente, então:
e) 1 e 1/2
f  x   ax  b
Como f  3   2  3a  b  2  b  2  3a
ff(x)  x  1 f(x)  ax  b
 
f f 1  1 a(ax  b)  b  x  1
a a  b  b  1 a2 x  ab  b  x 2  1
a  ab  b  1
2
a2 x  ab  b  x 2  1
Mas, b  2  3a então : a2  1
a  a  2  3a   2  3a  1
2
a  1  a  1
2a  a  1  0
2 bb 1
Resolvendo a equação: 2b  1
1
1
a' = -1 ou a" = (nãoserve) b
2 2
R: Alternativa E.
Logo : b  5
Assim : f(x)   x  5, que corta o eixo x em 16) (ACAFE) Sendo f : IR  IR , definida por
f x  0  x  5 f  x   2x  2 , todas as alternativas estão corretas,
exceto.
R: 05 a) f(x) é uma função crescente.
b) O valor de f(0) é igual a 2.
13) (UDESC) Sejam as funções f e g dadas por x2
c) A função inversa de f é dada por f 1  x   .
f  x   x 3  2 e g  x   3 x  2 ; portanto, o valor 2

numérico de f  g  1  g  f  1 é: d) O gráfico f(x) é uma reta que intercepta o eixo OX no
ponto (1,0).
a) 2
b) 1 e) f(x) é positiva para x  1
c) 0
3  f(x)  2x  2  y  2x  2
d) 3
e) 1 x  2y  2
x2 x2
y  f 1(x) 
g( 1) 3 1  1 2 2
f(g( 1))  f(1)  13  2  1  x  1  f(1)  2.1  2  4
R: Alternativa D.
f( 1)  ( 1)2  2  3
g(f( 1))  g( 3) 3 1  1 17) Consideremos a função inversível f cujo gráfico é
visto abaixo.
| f(g( 1))  g(f( 1)) |  | 1  ( 1) | 0
R: Alternativa C.
A lei que define f 1  x  é:
a) y = 3x + 3/2
b) y = 2x - 3/2
5

6. MATEMÁTICA – A1
c) y = (3/2)x -3 01. Verdadeira
d) y = (2/3)x +2 y  x  3
e) y = -2x - 3/2 y  03
P1(0,2) y3  0,3 
P2 (3, 4) 02. Falsa, f é uma função decrescente pois a< 0.
Na inversa :
04. Verdadeira
P1(2,0)
g  x   x2  1
P2 (4,3)
g x  0
2a  b  0
f 1(x)  ax  b  
 4a  b  3 x2  1  0
2a  3 x2  1
3 x  1
a  b  3
2 08. Verdadeira
3x
f 1(x)  3
2
R: Alternativa C.
Im  g  y   / y  1
18) A função inversa de uma função cujos pares são
(x, y) é uma outra função em que os pares são
invertidos, isto é, x da original passa a ser y e vice-
2x  1
versa. Encontre a função inversa de y  .
3x
16. Verdadeira
3x  1 y  x  3
a) y 1 
2x x  y  3
3x
b) y 1  y  x  3
2x  3
2x  1 f 1  x    x  3
c) y 1 
x 32. Verdadeira
d) 1
y 
1  
g f 1  g  1  3 
g  f 1   g  2 
2x
1 1
y 
g  f 1   22  1
e)
3x  2
g  f 1   3
2x  1
y 64. Falsa.
3x
2y  1 
x b yv  
3y xv   4a
x.3y  2y  1
2a
0 yv 
0 2
 4.1.  1 
3xy  2y  1 xv   4.1
2
y  3x  2   1 xv  0 4
yv  
 1  4
y  y v  1
 3x  2 
1 V  0, 1
Logo: y 1 
3x  2 Resposta: (VFVVVVF) 61.
19) (UFSC) Sejam f e g funções de R em R definidas
por: f(x) = -x + 3 e g(x) = x2 – 1. Determine a soma
dos números associados à(s) proposição (ões)
VERDADEIRA(S).
01. A reta que representa a função f intercepta o eixo das
ordenadas em (0,3).
02. f é uma função crescente.
04. –1 e +1 são os zeros da função g.
08. Im(g) = {y  R / y  -1}.
16. A função inversa da f é definida por f 1( x )   x  3 .
32. O valor de g( f (1)) é 3.
64. O vértice do gráfico de g é o ponto (0,0).
6

7. MATEMÁTICA – A1
20) (UFSC) – Sendo f : IR     IR    definida por
1 1 GABARITO
x
f (x)  y  , determine a soma dos números
x 1 AULAS 10 e 11
associados às afirmativas VERDADEIRAS.
01. O gráfico de f(x) é uma reta. 01) D
02. f ( x ) é uma função injetora. 02) C
x 03) B
04. Sua inversa é f 1  . 04) E
x 1
05) C
08. f ( x ) é uma função par. 06) B
16. O valor de f(2) é igual a 2. 07) D
32. f ( x ) é uma função bijetora. 08) B
09) C
01. Falsa. 10) A
11) C
12) 05
13) C
14) 15
15) E
16) D
17) C
18) E
19) 61
20) 54
02. Verdadeira. Como x1  x 2  f  x1   f  x 2  a função é
injetora.
04. Verdadeira.
x
y
x 1
y
x
y 1
x.y  x  y
x.y  y  x
y  x  1  x
x
y  f x 
x 1
08. Falsa.
f  x   f  x 
x x

x  1 x  1
x x

x  1   x  1
x x

x 1 x 1
16. Verdadeira
2
f  2 
2 1
f  2  2
32. Verdadeira.
Como Im    1 e o CD    1 a função é
sobrejetora.
Como a função é injetora, a função é bijetora.
Resposta: (FVVFVV) 54.
7