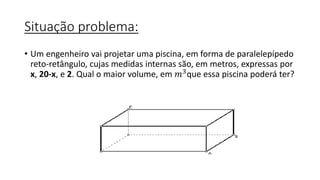
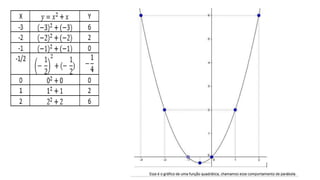
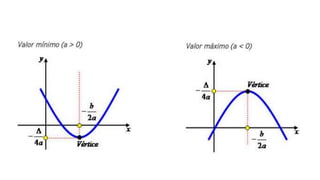
O documento introduz o conceito de função quadrática e apresenta exemplos para ilustrar suas principais características. É descrito que uma função quadrática é toda função na forma f(x)=ax2+bx+c, onde a, b e c são números reais e a ≠ 0. Além disso, são explicados os conceitos de zeros da função, vértice da função e ponto onde a função corta o eixo y. Finalmente, é retomado o problema inicial sobre o projeto de uma piscina para aplicar os conceitos aprendidos.

1. Função quadrática
Uma breve introdução ao estudo das funções quadráticas.

2. Situação problema:
• Um engenheiro vai projetar uma piscina, em forma de paralelepípedo
reto-retângulo, cujas medidas internas são, em metros, expressas por
x, 20-x, e 2. Qual o maior volume, em 𝑚3que essa piscina poderá ter?

3. Função quadrática:
• Uma função quadrática é toda função 𝑓: 𝐼𝑅  𝐼𝑅 que tem a forma
irredutível 𝑓 𝑥 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐, onde a,b e c são números reais e
𝑎 ≠ 0.
• Nota: Faz-se necessário que o coeficiente a seja diferente de zero,
pois se fosse igual a zero teríamos uma função linear.
• Quando em uma equação temos todos os coeficientes (a,b e c)
dizemos que a equação está completa, se não dizemos que é
incompleta.

4. Exemplos:
1. Qual das funções abaixo representa uma função
quadrática?
a) 𝑓 𝑥 = 3𝑥 + 2𝑥2
b) 𝑓 𝑥 = 𝑥3
+ 2𝑥 + 1
c) 𝑓 𝑥 = 𝑥 − 1 . (𝑥 + 2)
d) 𝑓 𝑥 = 3𝑥2
+ 4𝑥 + 1

5. Gráfico de uma função quadrática
• Agora veremos como fica o gráfico de uma função
quadrática, para isso, sem perca de generalidade
consideraremos a função 𝑦 = 𝑥2
+ 𝑥
• Primeiro atribuiremos alguns valores para x e em
seguida calculamos o valor para y, após isso ligamos
os pontos (x,y) encontrados.

7. •Em um gráfico de uma função quadrática temos
alguns pontos que merecem destaques, são eles:
1. Zeros da função
2. Vértice da função
3. Ponto onde o gráfico corta o eixo y
Vamos estudar os três itens acima e buscando
assim melhor entendimento do que eles
significam.

8. 1. Zeros ou raízes de uma função. (Definição geral)
• Seja 𝑓 𝑥 uma função, dizemos que b é raiz de uma função quando
𝑓 𝑏 = 0.
• A interpretação geométrica de uma raiz de uma função é o ponto
onde a função corta o eixo x. (Veja o exemplo anterior)

9. Fórmula de Bhaskara.
• No que se refere as raízes de uma função quadrática, temos diversos
métodos para encontrar as raízes, um método bastante comum é
recorrer a Fórmula de Bhaskara.
𝑥 =
−𝑏 ± 𝚫
2. 𝑎
Onde:
𝚫 = 𝑏2 − 4. 𝑎. 𝑐

10. Exemplo
• Qual são os zeros da função dada por 𝑓 𝑥 = 𝑥2 + 𝑥?

11. 2. Vértice de uma função quadrática
• Definição: O vértice de uma parábola, também chamado de ponto de
retorno é o ponto do gráfico onde a parábola “muda” de sentido, isto
é, se ela está crescente (decrescente), passa a ser decrescente
(crescente).
Em uma função 𝑦 = 𝑎𝑥2 − 𝑏𝑥 + 𝑐 temos que o vértice é dado por:
𝑉 (
−𝑏
2𝑎
;
−𝛥
4𝑎
)

12. •Se 𝑎 < 0 , dizemos que o vértice é o valor
máximo da função, dizemos também que a
função tem concavidade voltada para baixo.
•Se 𝑎 > 0 , dizemos que o vértice é o valor
mínimo da função, dizemos também que a
função tem concavidade voltada para cima.

14. Exemplo
• Qual o vértice da função quadrática dada por 𝑦 = 𝑥2 + 𝑥?

15. 3. Ponto onde a função corta o eixo y
•Este é o mais simples em nosso estudo. Em uma
função do segundo grau 𝑓 𝑥 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐
para sabermos onde a função corta o eixo y
basta fazermos 𝑥 = 0

16. Exemplo:
• Onde a função quadrática dada por 𝑦 = 4𝑥2 + 5𝑥 + 3 corta o corta o
eixo y?

17. Retornando ao início...
• Neste ponto do estudo da teoria já temos condições de resolver o
problema que motivou o estudo das funções quadráticas.
• Um engenheiro vai projetar uma piscina, em forma de paralelepípedo
reto-retângulo, cujas medidas internas são, em metros, expressas por
x, 20-x, e 2. Qual o maior volume, em 𝑚3que essa piscina poderá ter?

18. Atividade avaliativa