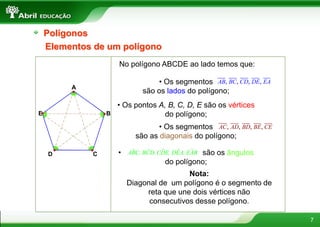
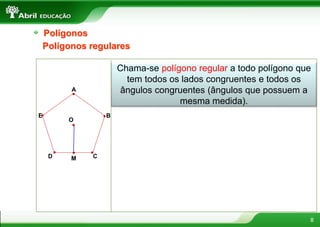
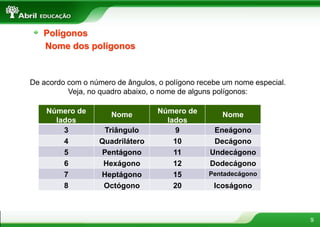
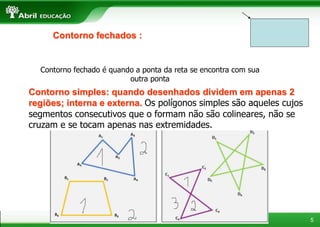
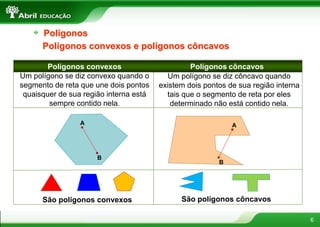
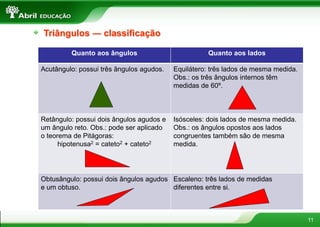
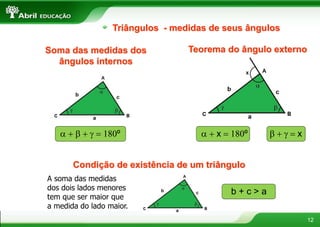
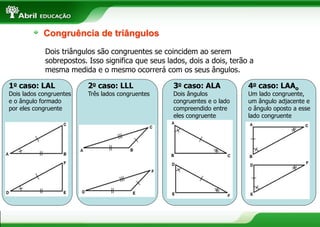
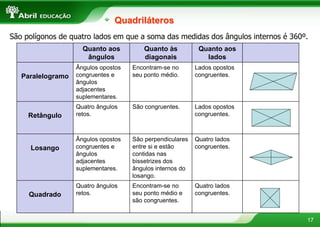
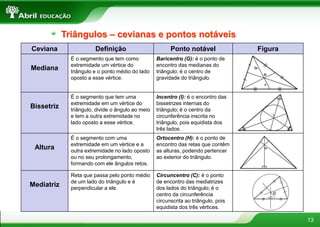
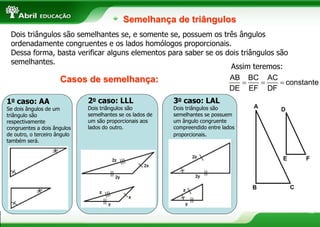
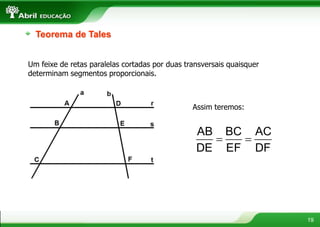
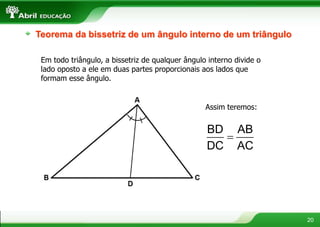
1. O documento discute vários conceitos geométricos como polígonos, triângulos, quadriláteros e suas propriedades. 2. Polígonos são figuras planas formadas por linhas fechadas e simples. Triângulos podem ser classificados de acordo com seus ângulos ou lados. 3. Os teoremas de Tales e da bissetriz de um ângulo interno de um triângulo tratam de proporcionalidade entre segmentos.

1. Polígonos
1
Geometria plana
Índice
Esquadros de madeira ― www.ser.com.br
Semelhança de triângulos
Triângulos
Congruência de triângulos
Quadriláteros
Teorema de Tales
Teorema da bissetriz de um ângulo
interno de um triângulo
Relações métricas no triângulo retângulo

2. 2
Polígonos
Definição
Chama-se polígono toda figura plana formado por linhas
poligonal fechadas e simples juntamente com os pontos da
região interna que essa linha determina.
As figuras a seguir são polígonos
As figuras a seguir não são polígonos

3. 3
Plano
Não plano

4. 4

5. 5
Contorno fechados :
Contorno fechado é quando a ponta da reta se encontra com sua
outra ponta
Contorno simples: quando desenhados dividem em apenas 2
regiões; interna e externa. Os polígonos simples são aqueles cujos
segmentos consecutivos que o formam não são colineares, não se
cruzam e se tocam apenas nas extremidades.

6. 6
Um polígono se diz convexo quando o
segmento de reta que une dois pontos
quaisquer de sua região interna está
sempre contido nela.
Polígonos convexos e polígonos côncavos
Polígonos convexos Polígonos côncavos
Um polígono se diz côncavo quando
existem dois pontos de sua região interna
tais que o segmento de reta por eles
determinado não está contido nela.
A
B
A
B
São polígonos convexos São polígonos côncavos
Polígonos

7. 7
Polígonos
Elementos de um polígono
No polígono ABCDE ao lado temos que:
A
B
CD
E
• Os segmentos
são os lados do polígono;
, , , ,AB BC CD DE EA
• Os pontos A, B, C, D, E são os vértices
do polígono;
• Os segmentos
são as diagonais do polígono;
, , , ,AC AD BD BE CE
• são os ângulos
do polígono;
ˆ ˆˆ ˆ ˆABC, BCD, CDE, DEA, EAB
Nota:
Diagonal de um polígono é o segmento de
reta que une dois vértices não
consecutivos desse polígono.

8. 8
Polígonos
Chama-se polígono regular a todo polígono que
tem todos os lados congruentes e todos os
ângulos congruentes (ângulos que possuem a
mesma medida).
Polígonos regulares
A
B
CD
E
M
O

9. 9
Nome dos polígonos
De acordo com o número de ângulos, o polígono recebe um nome especial.
Veja, no quadro abaixo, o nome de alguns polígonos:
Número de
lados
Nome Número de
lados
Nome
3 Triângulo 9 Eneágono
4 Quadrilátero 10 Decágono
5 Pentágono 11 Undecágono
6 Hexágono 12 Dodecágono
7 Heptágono 15 Pentadecágono
8 Octógono 20 Icoságono
Polígonos

10. 10
Polígonos
Soma das medidas
dos ângulos internos:
 180º 2iS n 
Soma das medidas
dos ângulos externos:
360ºeS 
Ângulos internos de
um polígono regular:
 180º 2
oui
i i
nS
a a
n n

 
Ângulos externos de
um polígono regular:
360º
oue
e e
S
a a
n n
 
Número de diagonais
de um polígono:
 3
2
n n
d



11. 11
Triângulos ― classificação
Quanto aos ângulos Quanto aos lados
Acutângulo: possui três ângulos agudos. Equilátero: três lados de mesma medida.
Obs.: os três ângulos internos têm
medidas de 60º.
Retângulo: possui dois ângulos agudos e
um ângulo reto. Obs.: pode ser aplicado
o teorema de Pitágoras:
hipotenusa2 = cateto2 + cateto2
Isósceles: dois lados de mesma medida.
Obs.: os ângulos opostos aos lados
congruentes também são de mesma
medida.
Obtusângulo: possui dois ângulos agudos
e um obtuso.
Escaleno: três lados de medidas
diferentes entre si.

12. 12
Triângulos - medidas de seus ângulos
Soma das medidas dos
ângulos internos
Teorema do ângulo externo
Condição de existência de um triângulo
a + b + g  180º a + x  180º b + g  x
A soma das medidas
dos dois lados menores
tem que ser maior que
a medida do lado maior.
b + c > a

13. 13
Triângulos – cevianas e pontos notáveis
Ceviana Definição Ponto notável Figura
Mediana
É o segmento que tem como
extremidade um vértice do
triângulo e o ponto médio do lado
oposto a esse vértice.
Baricentro (G): é o ponto de
encontro das medianas do
triângulo; é o centro de
gravidade do triângulo.
Bissetriz
É o segmento que tem uma
extremidade em um vértice do
triângulo, divide o ângulo ao meio
e tem a outra extremidade no
lado oposto a esse vértice.
Incentro (I): é o encontro das
bissetrizes internas do
triângulo; é o centro da
circunferência inscrita no
triângulo, pois equidista dos
três lados.
Altura
É o segmento com uma
extremidade em um vértice e a
outra extremidade no lado oposto
ou no seu prolongamento,
formando com ele ângulos retos.
Ortocentro (H): é o ponto de
encontro das retas que contêm
as alturas, podendo pertencer
ao exterior do triângulo.
Mediatriz
Reta que passa pelo ponto médio
de um lado do triângulo e é
perpendicular a ele.
Circuncentro (C): é o ponto
de encontro das mediatrizes
dos lados do triângulo; é o
centro da circunferência
circunscrita ao triângulo, pois
equidista dos três vértices.

14. 14
Congruência de triângulos
Dois triângulos são congruentes se coincidem ao serem
sobrepostos. Isso significa que seus lados, dois a dois, terão a
mesma medida e o mesmo ocorrerá com os seus ângulos.
1o caso: LAL
Dois lados congruentes
e o ângulo formado
por eles congruente
3o caso: ALA
Dois ângulos
congruentes e o lado
compreendido entre
eles congruente
4o caso: LAAo
Um lado congruente,
um ângulo adjacente e
o ângulo oposto a esse
lado congruente
2o caso: LLL
Três lados congruentes

15. 15
Semelhança de triângulos
Dois triângulos são semelhantes se, e somente se, possuem os três ângulos
ordenadamente congruentes e os lados homólogos proporcionais.
Dessa forma, basta verificar alguns elementos para saber se os dois triângulos são
semelhantes.
1o caso: AA
Se dois ângulos de um
triângulo são
respectivamente
congruentes a dois ângulos
de outro, o terceiro ângulo
também será.
3o caso: LAL
Dois triângulos são
semelhantes se possuem
um ângulo congruente
compreendido entre lados
proporcionais.
2o caso: LLL
Dois triângulos são
semelhantes se os lados de
um são proporcionais aos
lados do outro.
Casos de semelhança:
Assim teremos:
  
AB BC AC
constante
DE EF DF

16. 16
Relações métricas no triângulo retângulo
Considere um triângulo ABC, retângulo em A, e o segmento
perpendicular ao lado , com D em .
AD
BC BC
Definições dos segmentos:






BC hipotenusa (medida "a")
AB cateto (medida "c")
AC cateto (medida "b")
BD projeção do cateto AB
sobre a hipotenusa (medida "m")
DC projeção do cateto AC
sobre a hipotenusa (medida "n")
AD altura relativa à
hipotenusa (medida "h")
Assim teremos:
2 2 2
2
2
2
 +
  
 
 
 
a b c
a h b c
b m a
c n a
h m n

17. 17
Quadriláteros
Quanto aos
ângulos
Quanto às
diagonais
Quanto aos
lados
Paralelogramo
Ângulos opostos
congruentes e
ângulos
adjacentes
suplementares.
Encontram-se no
seu ponto médio.
Lados opostos
congruentes.
Retângulo
Quatro ângulos
retos.
São congruentes. Lados opostos
congruentes.
Losango
Ângulos opostos
congruentes e
ângulos
adjacentes
suplementares.
São perpendiculares
entre si e estão
contidas nas
bissetrizes dos
ângulos internos do
losango.
Quatro lados
congruentes.
Quadrado
Quatro ângulos
retos.
Encontram-se no
seu ponto médio e
são congruentes.
Quatro lados
congruentes.
São polígonos de quatro lados em que a soma das medidas dos ângulos internos é 360º.

18. 18
Quadriláteros
Os trapézios são quadriláteros que têm apenas um par de
lados paralelos, chamados base maior e base menor.
Trapézio retângulo
É todo trapézio que tem dois
ângulos retos. Nele, um dos
lados que não é base é
perpendicular às duas bases.
Trapézio isósceles
É todo trapézio que tem dois
lados não paralelos
congruentes.

19. 19
Teorema de Tales
Um feixe de retas paralelas cortadas por duas transversais quaisquer
determinam segmentos proporcionais.
Assim teremos:
 
AB BC AC
DE EF DF

20. 20
Teorema da bissetriz de um ângulo interno de um triângulo
Em todo triângulo, a bissetriz de qualquer ângulo interno divide o
lado oposto a ele em duas partes proporcionais aos lados que
formam esse ângulo.
Assim teremos:

BD AB
DC AC