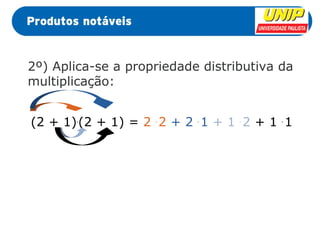
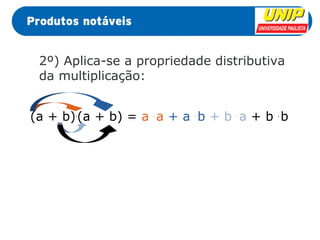
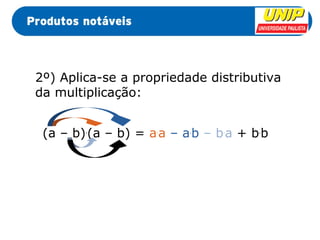
Este documento apresenta dois produtos notáveis: (1) o quadrado da soma de dois termos, (a + b)2, que é igual a a2 + 2ab + b2 e (2) o quadrado da diferença de dois termos, (a - b)2, que é igual a a2 - 2ab + b2. Exemplos numéricos e algébricos são fornecidos para ilustrar cada produto notável.