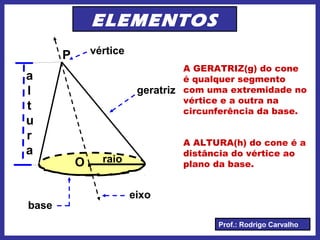
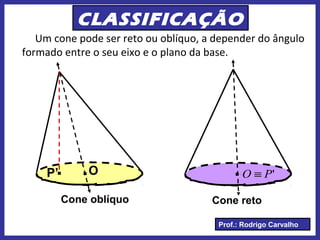
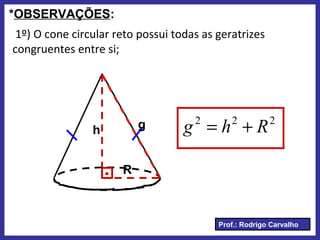
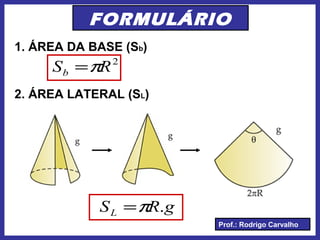
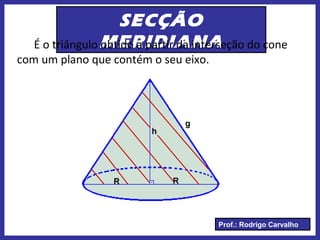
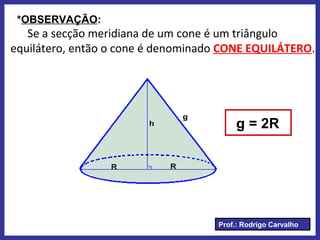
Este documento define e descreve as características de um cone circular. Apresenta os elementos fundamentais de um cone, como vértice, base, eixo e geratriz. Classifica cones como retos ou oblíquos e fornece fórmulas para cálculo de área total, lateral e volume.

1. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
CONES

2. Prof.: Rodrigo Carvalho
DEFINIÇÃO
Consideremos um círculo contido num plano e um
ponto P fora desse plano. Chamamos de CONE
CIRCULAR, ou simplesmente CONE, a reunião de todos
os segmentos com uma extremidade em P e a outra
num ponto qualquer do círculo.

3. Prof.: Rodrigo Carvalho
ELEMENTOS
P
O .
base
eixo
vértice
geratriz
a
l
t
u
r
a
A ALTURA(h) do cone é a
distância do vértice ao
plano da base.
A GERATRIZ(g) do cone
é qualquer segmento
com uma extremidade no
vértice e a outra na
circunferência da base.
raio

4. Prof.: Rodrigo Carvalho
CLASSIFICAÇÃO
Um cone pode ser reto ou oblíquo, a depender do ângulo
formado entre o seu eixo e o plano da base.
O. .
Cone oblíquo Cone reto
'PO ≡.P’

5. Prof.: Rodrigo Carvalho
*OBSERVAÇÕES:
1º) O cone circular reto possui todas as geratrizes
congruentes entre si;
.
h
R
g 222
Rhg +=

6. Prof.: Rodrigo Carvalho
2º) O cone circular reto também é chamado de cone de revolução,
pois é gerado pela rotação completa de um triângulo retângulo em
torno de um eixo que contém um de seus catetos.
.

7. Prof.: Rodrigo Carvalho
FORMULÁRIO
1. ÁREA DA BASE (Sb)
2
RSb π=
2. ÁREA LATERAL (SL)
gRSL .π=

8. Prof.: Rodrigo Carvalho
3. ÁREA TOTAL (St)
É a soma da área da base com a área lateral.
Lbt SSS +=
gRRSt .2
ππ +=
)( gRRSt +=π

9. Prof.: Rodrigo Carvalho
4. VOLUME (V)
É um terço do produto da área da base pela altura do cone.
hSV b .
3
1
=
hRV .
3
1 2
π=
Exemplo1: Num cone de revolução de geratriz 13cm e raio
da base 5cm, calcule a altura, a área total e o ângulo da
superfície lateral planificada, em radianos.

10. Prof.: Rodrigo Carvalho
SECÇÃO
MERIDIANAÉ o triângulo obtido a partir da interseção do cone
com um plano que contém o seu eixo.

11. Prof.: Rodrigo Carvalho
Se a secção meridiana de um cone é um triângulo
equilátero, então o cone é denominado CONE EQUILÁTERO.
*OBSERVAÇÃO:
g = 2R

12. Prof.: Rodrigo Carvalho
Sugestão de exercícios:
CAPÍTULO 6
Questões: 181, 184, 187, 190 e 192.