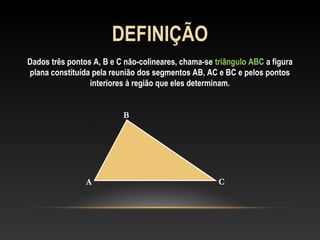
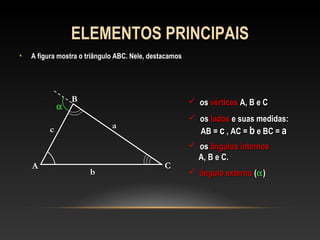
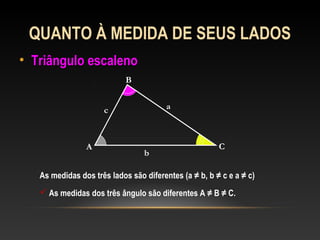
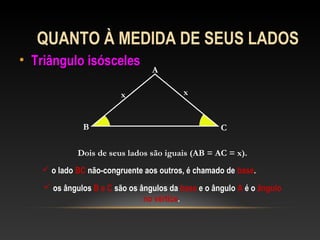
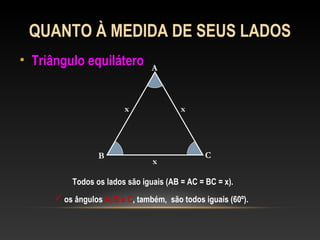
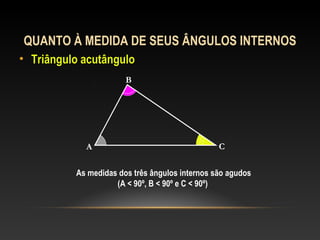
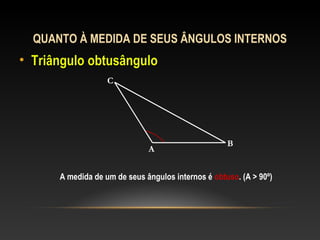
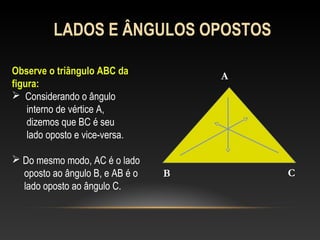
Este documento apresenta uma introdução sobre triângulos, definindo-os como figuras formadas por três segmentos de reta e três vértices. Em seguida, classifica os triângulos de acordo com a medida de seus lados e ângulos internos, distinguindo triângulos escaleno, isósceles, equilátero, acutângulo, retângulo e obtusângulo.

1. Entre as figuras
geométricas o triângulo
merece atenção
especial,
principalmente pelas
suas aplicações
práticas.

2. Prof. Jorge
ESTUDO DOS
TRIÂNGULOS

3. DEFINIÇÃO
Dados três pontos A, B e C não-colineares, chama-se triângulo ABC a figura
plana constituída pela reunião dos segmentos AB, AC e BC e pelos pontos
interiores à região que eles determinam.
A
B
C

4. ELEMENTOS PRINCIPAIS
• A figura mostra o triângulo ABC. Nele, destacamos
A
B
C
a
b
c
 osos vérticesvértices A, B e CA, B e C
 osos ladoslados e suas medidas:e suas medidas:
AB =AB = cc , AC =, AC = bb e BC =e BC = aa
 osos ângulos internosângulos internos
A, B e C.A, B e C.
α
 ângulo externoângulo externo ((αα))

5. Prof. Jorge
CLASSIFICAÇÃO
DOS TRIÂNGULOS

6. QUANTO À MEDIDA DE SEUS LADOS
• Triângulo escalenoTriângulo escaleno
A
B
C
a
b
c
As medidas dos três lados são diferentes (a ≠ b, b ≠ c e a ≠ c)
 As medidas dos três ângulo são diferentes A ≠ B ≠ C.

7. QUANTO À MEDIDA DE SEUS LADOS
• Triângulo isóscelesTriângulo isósceles
A
B C
xx
Dois de seus lados são iguais (AB = AC = x).
 o lado BC não-congruente aos outros, é chamado de base.
 os ângulos B e C são os ângulos da base e o ângulo A é o ângulo
no vértice.

8. QUANTO À MEDIDA DE SEUS LADOS
• Triângulo equiláteroTriângulo equilátero A
B C
xx
Todos os lados são iguais (AB = AC = BC = x).
 os ângulos A, B e C, também, são todos iguais (60º).
x

9. QUANTO À MEDIDA DE SEUS ÂNGULOS INTERNOS
• Triângulo acutânguloTriângulo acutângulo
A
B
C
As medidas dos três ângulos internos são agudos
(A < 90º, B < 90º e C < 90º)

10. QUANTO À MEDIDA DE SEUS ÂNGULOS INTERNOS
• Triângulo retânguloTriângulo retângulo
A B
C
Um de seus ângulos internos é reto. (A = 90º)
 O lado BC é chamado de hipotenusa; os outros dois são
chamados catetos.

11. QUANTO À MEDIDA DE SEUS ÂNGULOS INTERNOS
• Triângulo obtusânguloTriângulo obtusângulo
A
B
C
A medida de um de seus ângulos internos é obtuso. (A > 90º)

12. LADOS E ÂNGULOS OPOSTOS
Observe o triângulo ABC da
figura:
 Considerando o ângulo
interno de vértice A,
dizemos que BC é seu
lado oposto e vice-versa.
 Do mesmo modo, AC é o lado
oposto ao ângulo B, e AB é o
lado oposto ao ângulo C.
A
B C

13. Referências:
•IEZZI, Gelson; MACHADO,
Antonio; DOLCE, Osvaldo.
Geometria Plana-Conceitos básicos.
1ª edição. São Paulo: Atual, 2008.
•DANTE, Luiz Roberto. Matemática.
Ensino Médio. Projeto Múltiplo. São
Paulo: Ática: 2014.
•DOLCE, Osvaldo. Fundamentos de
Matemática elementar 9: geometria
plana. 8ª ed. São Paulo: Atual, 2005.
•GIOVANNI, José Rui; PARENTE,
Eduardo. Aprendendo Matemática.
São Paulo: FTD, 2007

14. CONDIÇÃO DE EXISTENCIA DE UM TRIÂNGULO
CONSTRUÇÕES NA FOLHA
EXERCÍCIOS DO LIVRO PGS 24 E 25