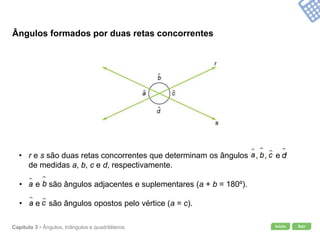
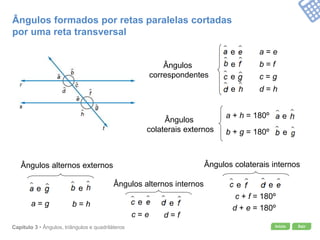
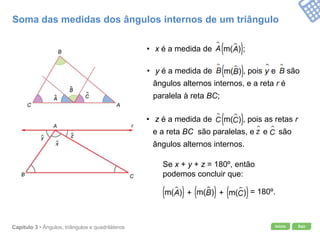
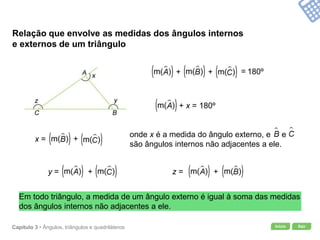
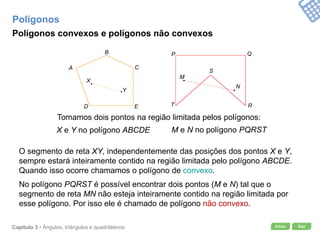
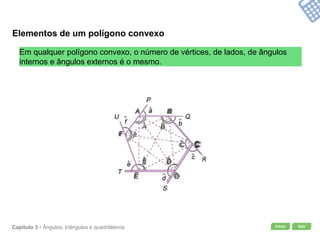
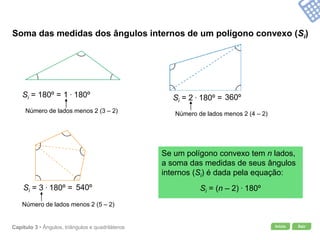
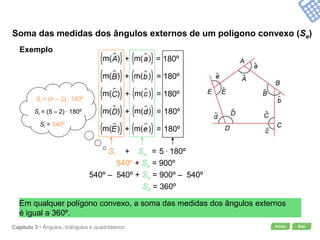
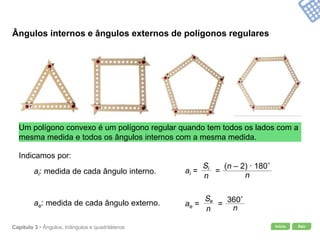
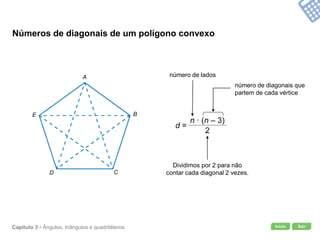
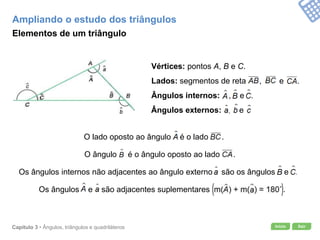
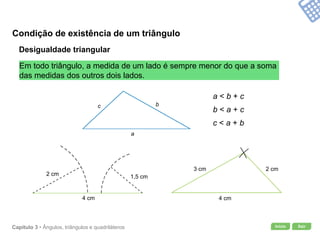
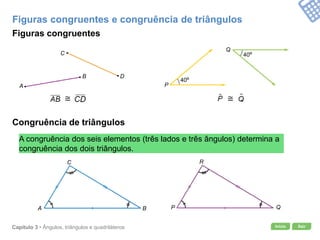
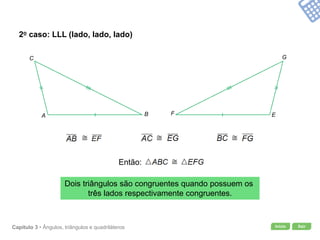
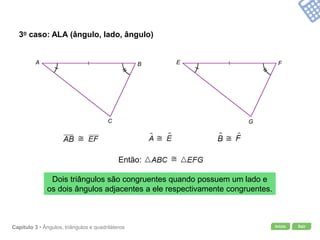
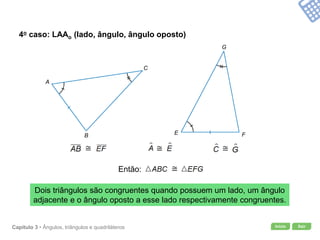
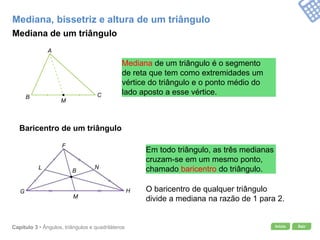
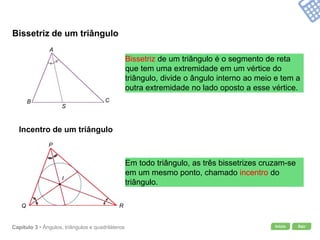
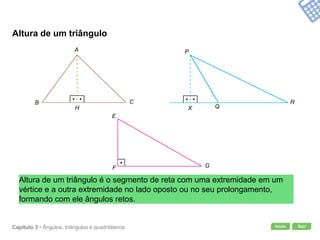
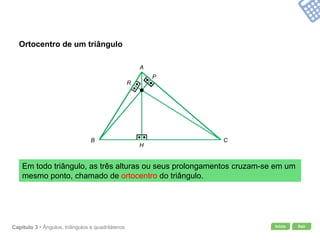
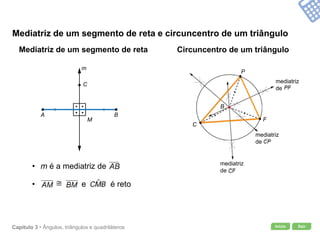
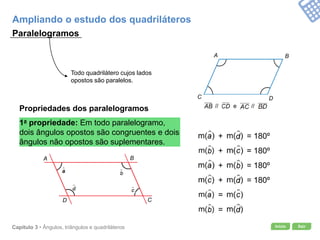
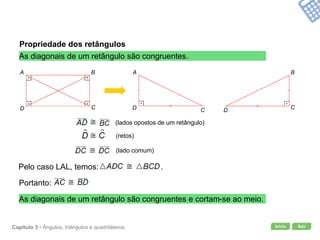
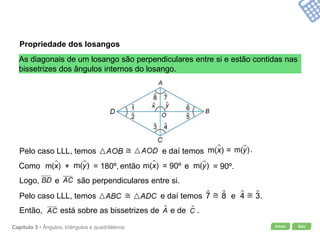
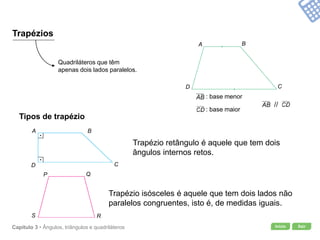
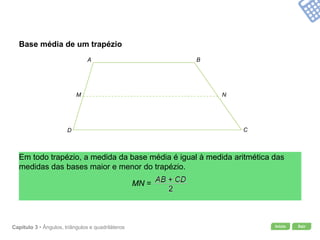
O documento apresenta conceitos geométricos como ângulos, triângulos, polígonos e quadriláteros. Inclui definições de ângulos opostos pelo vértice, soma dos ângulos internos de polígonos, elementos de triângulos e quadriláteros como paralelogramos e trapézios.