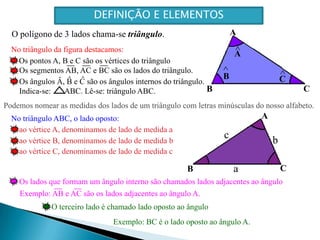
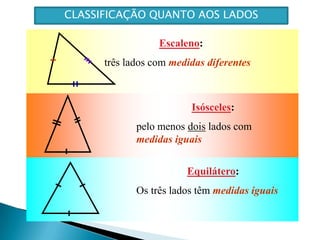
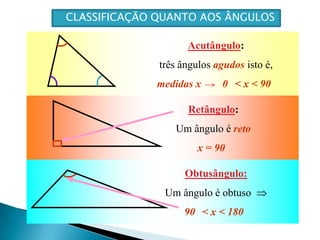
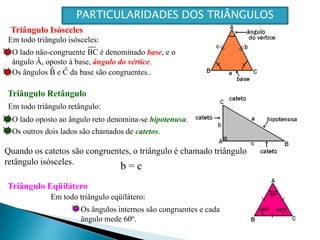
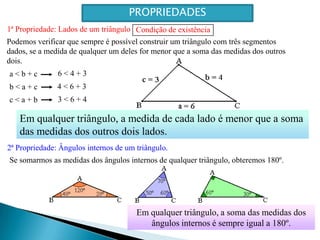
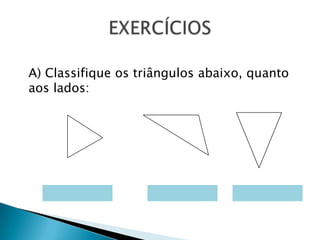
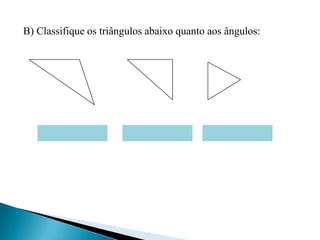
Este documento apresenta os conceitos básicos sobre triângulos, incluindo seus elementos, classificações de acordo com os lados e ângulos, e propriedades. É explicado que um triângulo possui três lados e três ângulos internos que somam 180°, e pode ser classificado como equilátero, isósceles ou escaleno dependendo da igualdade entre seus lados. O documento também fornece exemplos e exercícios sobre triângulos.

1. NO MUNDO DOS TRIÂNGULOS

2. OBSERVE AS FIGURAS ABAIXOTODAS ELAS POSSUEM A MESMA FORMA GEOMÉTRICA: SÃO TRIÂNGULOS

3. A Os pontos A, B e C são os vértices do triânguloOs segmentos AB, AC e BC são os lados do triângulo.^^Os ângulos Â, B e C são os ângulos internos do triângulo.Indica-se: ABC. Lê-se: triângulo ABC.C B Aao vértice A, denominamos de lado de medida a^ao vértice B, denominamos de lado de medida b^A C ^ao vértice C, denominamos de lado de medida cB CBOs lados que formam um ângulo interno são chamados lados adjacentes ao ânguloExemplo: AB e AC são os lados adjacentes ao ângulo A.O terceiro lado é chamado lado oposto ao ânguloExemplo: BC é o lado oposto ao ângulo A.DEFINIÇÃO E ELEMENTOSO polígono de 3 lados chama-se triângulo.No triângulo da figura destacamos:Podemos nomear as medidas dos lados de um triângulo com letras minúsculas do nosso alfabeto.No triângulo ABC, o lado oposto:cba

4. Escaleno:três lados com medidasdiferentesIsósceles:pelo menos dois lados com medidas iguaisEquilátero:Os três lados têm medidas iguaisCLASSIFICAÇÃO QUANTO AOS LADOS

5. Acutângulo:três ângulos agudos isto é, medidas x 0° < x < 90°Retângulo:Um ângulo é retox = 90°Obtusângulo:Um ângulo é obtuso  90° < x < 180° CLASSIFICAÇÃO QUANTO AOS ÂNGULOS

6. O lado não-congruente BC é denominado base, e o ângulo Â, oposto à base, ângulo do vértice.^^Os ângulos B e C da base são congruentes..O lado oposto ao ângulo reto denomina-se hipotenusa.Os outros dois lados são chamados de catetos.Quando os catetos são congruentes, o triângulo é chamado triângulo retângulo isósceles.b = cOs ângulos internos são congruentes e cada ângulo mede 60º.PARTICULARIDADES DOS TRIÂNGULOSTriângulo IsóscelesEm todo triângulo isósceles:Triângulo RetânguloEm todo triângulo retângulo:Triângulo EqüiláteroEm todo triângulo eqüilátero:

7. CondiçãodeexistênciaPROPRIEDADES1ª Propriedade: Lados de um triânguloPodemos verificar que sempre é possível construir um triângulo com três segmentos dados, se a medida de qualquer um deles for menor que a soma das medidas dos outros dois.6 < 4 + 3a < b + c 4 < 6 + 3b < a + c 3 < 6 + 4c < a + b Em qualquer triângulo, a medida de cada lado é menor que a soma das medidas dos outros dois lados.2ª Propriedade: Ângulos internos de um triângulo.Se somarmos as medidas dos ângulos internos de qualquer triângulo, obteremos 180º.Em qualquer triângulo, a soma das medidas dos ângulos internos é sempre igual a 180º.

8. A) Classifique os triângulos abaixo, quanto aos lados:EXERCÍCIOS

9. B) Classifique os triângulos abaixo quanto aos ângulos:

10. C) Faça uma pesquisa no site abaixo e cole abaixo objetos que tenham forma de triângulos.http://www.google.com.br/webhp?rlz=1R2GFRE_pt-BRBR357&hl=pt-BR&source=hp&btnG=Pesquisa+Google

11. Acesse o site abaixo e realize algumas atividades sobre TRIÂNGULOShttp://www.malhatlantica.pt/saobruno/Ano08/mat/triang_html/triang_nocoes.htm

12. VAMOS FALAR AGORA DOS TRIÂNGULOS EQÜILÁTEROS ...Você lembra o que é bissetriz e mediatriz de um triângulo?Acesse o site a seguir e veja as definições ...http://pt.wikipedia.org/wiki/Tri%C3%A2nguloNa próxima aula vamos construir e explorar algumas atividades com triângulos utilizando o software Régua e Compasso, acessando os programas instalados no computador e através do tutorial que será apresentado a você.