Este documento apresenta uma lista de exercícios de matemática com 25 questões sobre geometria espacial, incluindo cubos, paralelepípedos, cilindros e prisma. As questões abordam cálculos de volumes, áreas, razões e propriedades geométricas destes sólidos.







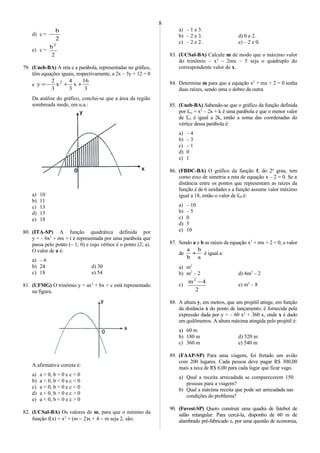
![devo aproveitar o muro do quintal (veja figura). Quais
devem ser as dimensões dessa quadra para que sua área
seja máxima?
a) x = 20 m e y = 10 m
b) x = 15 m e y = 30 m
c) x = 12 m e y = 18 m
d) x = 10 m e y = 10 m
e) x = 8 m e y = 30 m
91. Dispõe-se de uma folha de papel retangular medindo
20 cm de largura por 24 cm de comprimento. Deseja-
se recortar em cada quina da folha quatro quadrados
iguais (veja figura). Quanto deve medir o lado de cada
quadrado para que a área da região sombreada seja
máxima?
a) 4,5 cm
b) 5 cm
c) 5,5 cm
d) 6 cm
e) 6,5 cm
92. Um grupo de estudantes de meteorologia pesquisa as
variações bruscas de temperatura numa certa cidade.
Após longa coleta de dados, conclui-se que, às t horas
da madrugada, a temperatura, em um determinado dia,
foi dada por C(t) =
6
t2
− + 4t + 10, em graus Celsius.
Quanto aumentou ou diminuiu a temperatura, nesse dia,
entre 18 e 21 horas?
93. (Consultec-BA) O trinômio ax2
+ bx + c é negativo,
∀x, se:
a) a > 0 e ∆ < 0
b) a < 0 e ∆ > 0
c) a > 0 e ∆ > 0
d) a < 0 e ∆ < 0
94. (Consultec-BA) Se uma equação da forma ax2
+ bx + c = 0,
a ≠ 0, apresenta raízes reais de sinais contrários, então:
a) c / a > 0
b) – b / a > 0
c) c / a < 0
d) a / b > 0
95. Determine o domínio da seguinte função:
( )5xxy −=
96. Determine o domínio da seguinte função:
4x
2x
y
+
−
=
97. (PUC-SP) Os valores de m R, para os quais o domínio da
função f(x) =
mmxx2
1
2
+−
é R, são:
a) 0 < m < 8
b) m > 10
c) m > 0
d) 1 < m < 2
e) 0 ≤ m ≤ 7
98. (PUC-MG) A função quadrática f(x) = mx2
+ 2(m – 2)x +
m é positiva para qualquer valor real de x se:
a) m ≠ 0
b) 0 < m < 1
c) m > 0
d) m >
4
1
e) m > 1
99. Determine m de modo que, para qualquer que seja o
valor real de x, ocorra mx2
+ 4(m – 1)x + m – 1 > 0.
100.(Uneb-BA)
Da análise do gráfico onde estão representadas as
funções f(x) = – x + 2 e g(x) = x2
, pode-se concluir que
o conjunto-solução da inequação
( )
( )
1
xg
xf
< é:
a) ]– 2, 1[ – {0}
b) ]– 1, 2[ – {0} d) R – [– 1, 2]
c) R – [– 1, 1] e) R – [– 2, 1]
101.O conjunto solução da equação |3x – 2| = 3x – 2 é:
9](https://image.slidesharecdn.com/lmat05estudo-140515211407-phpapp02/85/L-mat05-estudo-com-9-320.jpg)
![a)
+∞;
3
2
b) R+ d)
+∞;
3
2
c) R e)
∞−
3
2
;
102.(ESPM-SP) Sabendo que |x|2
= x2
, resolver a
equação: x2
– 5 |x| + 6 = 0
103.(UEL-PR) No universo R, a equação |x|2
+ |x| – 12 = 0:
a) não admite soluções;
b) admite quatro soluções distintas;
c) admite duas soluções positivas;
d) admite duas soluções negativas;
e) admite duas soluções opostas entre si.
104.(Aman-RJ) O domínio de x em |x – 5| < 3 é:
a) não existe
b) 2 ≤ x ≤ 8 d) x < 2 ou x > 8
c) 2 < x < 8 e) x ≤ 2 ou x ≥ 8
105.(PUC-SP) O número de soluções da equação ||x| –
1| = 1, no universo R, é:
a) 0
b) 1
c) 2
d) 3
e) 4
GABARITO
0 1 2 3 4 5 6 7 8 9
0 – B 05 B C B D C B D
1 B 32 E 04 D 26 D D D 24
2 B 6 B 30 45 04 A D A A
3 B B C E E A C C A D
4 B E D A A 10 B 60 40 C
5 D A B B D B B A E D
6 D E B B A D C D C C
7 C B ↓ B D ↓ A B B C
8 E B C ↓ ↓ C E C E ↓
9 B C ↓ D C ↓ ↓ A E ↓
10 05 A ↓ E C D ↓ ↓ ↓ D
72. m =
2
3
75. m ≠ – 1
83. m = 1 ou m = – 5
84. m = ± 3
89. a) 90 000
b) 93 750
92. diminuiu 7,5o
C
95. ]– ∞; 0] ∪ [5; + ∞[
96. ]– ∞; – 4[ ∪ [2; + ∞[
99.
3
4
;1
102.{– 3, – 2, 2, 3}
10](https://image.slidesharecdn.com/lmat05estudo-140515211407-phpapp02/85/L-mat05-estudo-com-10-320.jpg)
















![t12
C
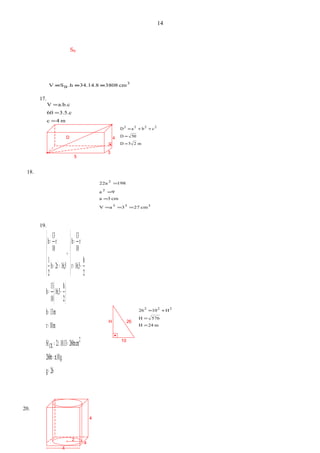
91.
( )[ ] ( )[ ]
( )
cm5,5
82
88
2a
b
vxx
88x8xA
2x20x22x24x2A
.x2x202..x2x242.A
máx
2
somb
22
somb
somb
=
−
−
=
−
==
+−=
−+−=
−+−=
92
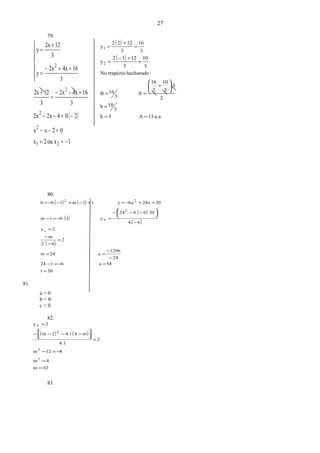
C7,5C20,5C28diminuiLogo,
C20,5C
104.21
6
21
C
C28C
104.18
6
18
C12
6
1
2
4
vx
(21)
2
(21)
(18)
2
(18)
°=°−°
°=
++−=
°=
++−==
−
−
=
93.
0Δ
e
0a
<
<
94.
0.
a
cLogo,
0ce0aou0ce0a
<
><<>
95.
( )
5ou x0x
05xx
05xx.
2
==
≥−
≥−
[[5;0],]D ∞∪∞−=
30
Logo, de t = 18 a t = 21, a temperatura diminui.](https://image.slidesharecdn.com/lmat05estudo-140515211407-phpapp02/85/L-mat05-estudo-com-30-320.jpg)
![-4 2
0
++
8
1
++
3
4
0m
0Δe0a
>
<>
96.
4x2x
04x02x
0
4x
2x
−≠=
≠+=−
≥
+
−
97.
( ) ( )( )
( )
.8m0Logo,8m
0m08mm
08mm
08m2m
0m24mΔ
0.Δfaçamos0,2aComo
0.Δe0aparaocorreisso
0mmx2x
2
1
2
2
2
<<=
==−
=−
<−
<−−=
<>=
<>
>+−
98.
( )[ ]
1m
1616m
04m1616m4m
1.mLogo,04m44mm4
1me0m04.m.m2m2Δ
22
22
2
>
−<−
<−+−
><−+−
>><−−=
99.
( )[ ] ( )
[
3
41;]S1m
3
4
m
6
17
m
14849Δ
047m3m
4)(01628m12m
01m4.m1m4
0Δe0m
2
1
2
2
2
==
=
±
=
=−=
<+−
<+−
<−−−
<>
100.
31
D = ] − ∞, − 4 [ ∪ [ 2; ∞ [
÷
ou
ou](https://image.slidesharecdn.com/lmat05estudo-140515211407-phpapp02/85/L-mat05-estudo-com-31-320.jpg)
![-2 10
0x1ou x2x
1]2;[RS0x02xx
0
x
x2x
01
x
2x
1
x
2x
21
22
2
2
2
2
≠=−=
−−=≠=+−−
<
−+−
<−
+−
<
+−
101.
Como o “modulando” é igual ao segundo membro, qualquer valor de x satisfaz a igualdade, desde que esse valor
pertença à condição de existência do 2o
membro.
∞=≥→≥− ;
3
2
S
3
2
x023x
102.
( ) ( )
2ou x3x
2xou3x
2
15
x
164.15Δ 2
±=±=
==
±
=
=−= −
103.
( )
3x
3x
2
71
x
49124.11Δ
2
±=
=
±−
=
=−−=
104.
2xe8x
35xe35x
><
−>−<−
105.
.reaissoluções3possuiequaçãoaLogo,
0xou2x
0xou2x
11xou11x
=±=
==
−=−=−
32
D = {X ∈ R / 2 < n < 8}
ou](https://image.slidesharecdn.com/lmat05estudo-140515211407-phpapp02/85/L-mat05-estudo-com-32-320.jpg)