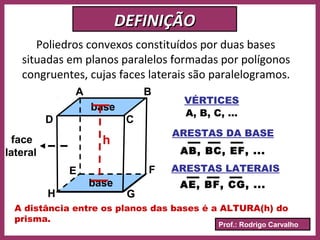
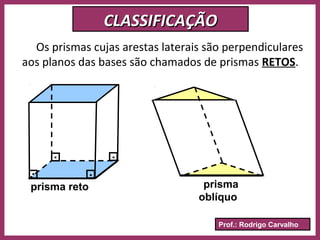
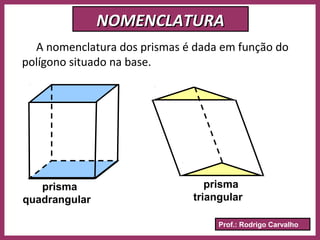
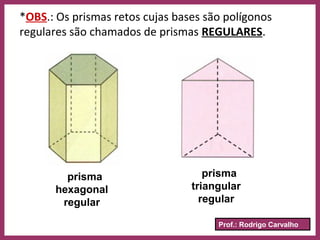
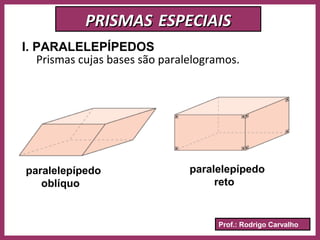
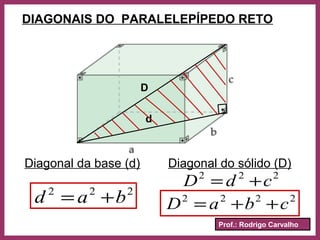
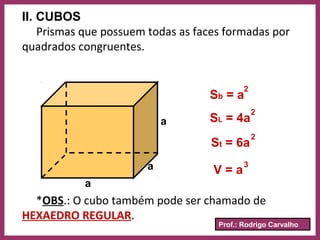
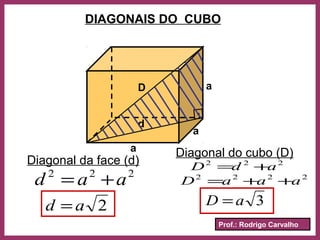
O documento define prisma como um poliedro convexo formado por duas bases paralelas congruentes e faces laterais em forma de paralelogramos. Descreve suas características principais como vértices, arestas, classificação, nomenclatura e fórmulas para calcular área e volume. Apresenta exemplos resolvidos e informações sobre paralelepípedos e cubos.

1. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho

2. Prof.: Rodrigo Carvalho
DEFINIÇÃODEFINIÇÃO
Poliedros convexos constituídos por duas bases
situadas em planos paralelos formadas por polígonos
congruentes, cujas faces laterais são paralelogramos.
base
base
A B
D
FE
C
GH
face
lateral
VÉRTICES
ARESTAS DA BASE
A, B, C, ...
AB, BC, EF, ...
ARESTAS LATERAIS
AE, BF, CG, ...
A distância entre os planos das bases é a ALTURA(h) do
prisma.
h

3. Prof.: Rodrigo Carvalho
CLASSIFICAÇÃOCLASSIFICAÇÃO
Os prismas cujas arestas laterais são perpendiculares
aos planos das bases são chamados de prismas RETOS.
prisma reto prisma
oblíquo
.
.
.
.

4. Prof.: Rodrigo Carvalho
NOMENCLATURANOMENCLATURA
A nomenclatura dos prismas é dada em função do
polígono situado na base.
prisma
quadrangular
prisma
triangular

5. Prof.: Rodrigo Carvalho
*OBS.: Os prismas retos cujas bases são polígonos
regulares são chamados de prismas REGULARES.
prisma
hexagonal
regular
prisma
triangular
regular

6. Prof.: Rodrigo Carvalho
FORMULÁRIOFORMULÁRIO
1. ÁREA DA BASE (Sb)
É a área do polígono que está na base.
2. ÁREA LATERAL (SL)
É a soma das áreas dos paralelogramos das faces laterais.
SL = 2p . h
3. ÁREA TOTAL (St)
É a soma das áreas das bases com a área lateral.
St = 2.Sb + SL

7. Prof.: Rodrigo Carvalho
4. VOLUME (V)
É o produto da área da base pela altura do prisma.
V = Sb . h
Exemplo1: Dado um prisma triangular regular de aresta da
base 4cm e altura 5cm, determine:
a) sua área da base;
b) sua área lateral;
c) sua área total;
d) seu volume.

8. Prof.: Rodrigo Carvalho
Exemplo2: Determine as medidas da altura e da aresta da
base de um prisma hexagonal regular, sabendo que seu
volume é 4 m e que a área de sua superfície lateral é de
12 m .
3
2
Exemplo3: (MACK – SP) Um prisma triangular regular tem
todas as arestas congruentes e 48 m de área lateral. Seu
volume vale:
2
3
3
3
3
3
m3e)16
m3d)4
mc)64
mb)32
ma)16

9. Prof.: Rodrigo Carvalho
(2010)

10. Prof.: Rodrigo Carvalho
PRISMASPRISMAS ESPECIAISESPECIAIS
I. PARALELEPÍPEDOS
Prismas cujas bases são paralelogramos.
paralelepípedo
oblíquo
paralelepípedo
reto

11. Prof.: Rodrigo Carvalho
* PARALELEPÍPEDOS RETOS
Paralelepípedos cujas bases são retângulos. Como
consequência, todas suas seis faces são retangulares.
Esses sólidos também podem ser chamados de
paralelepípedos retângulos ou ortoedros.
Sb = ab
SL = 2ac + 2bc
St = 2ab + 2ac + 2bc
V = abc

12. Prof.: Rodrigo Carvalho
DIAGONAIS DO PARALELEPÍPEDO RETO
d
D
.
Diagonal da base (d)
222
bad +=
Diagonal do sólido (D)
222
cdD +=
2222
cbaD ++=

13. Prof.: Rodrigo Carvalho
II. CUBOS
Prismas que possuem todas as faces formadas por
quadrados congruentes.
a
a
a
Sb = a
SL = 4a
St = 6a
V = a
2
2
2
3
*OBS.: O cubo também pode ser chamado de
HEXAEDRO REGULAR.

14. Prof.: Rodrigo Carvalho
DIAGONAIS DO CUBO
a
a
a
Diagonal da face (d)
d
222
aad +=
2ad =
Diagonal do cubo (D)
D
.
222
adD +=
2222
aaaD ++=
3aD =

15. Prof.: Rodrigo Carvalho
Exercícios:
01. Determine o volume do cubo cuja área mede 54 cm.
2
02. Um tanque em forma de paralelepípedo retângulo
possui comprimento 20 cm e largura 5 cm. Uma pedra é
arremessada no interior desse tanque, ficando totalmente
submersa, fazendo com que o nível de água aumente em
0,2 cm. Determine o volume dessa pedra.

16. Prof.: Rodrigo Carvalho
(2010)

17. Prof.: Rodrigo Carvalho
Sugestão de exercícios:
CAPÍTULO 3
Questões: 81, 83, 94, 105, 114, 117 e 118.