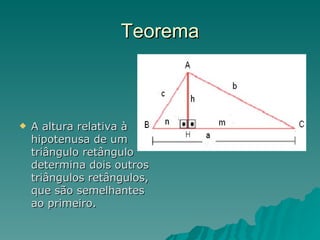
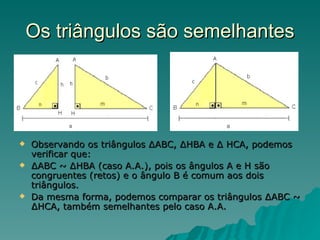
O documento discute as relações métricas em triângulos retângulos. Explica que um triângulo retângulo tem um ângulo reto e os lados adjacentes são chamados de catetos. A altura relativa à hipotenusa cria dois outros triângulos retângulos semelhantes onde as relações entre os lados seguem regras de proporcionalidade de acordo com a semelhança dos triângulos. Essas relações levam ao Teorema de Pitágoras.

1. Relações Métricas no Triângulo Retângulo Professora Lilene

2. O Triângulo Retângulo O triângulo retângulo possui um ângulo reto, ou seja, um ângulo cuja medida é 90º. Em um triângulo retângulo, o lado oposto ao ângulo reto é chamado hipotenusa e os lados adjacentes ao ângulo reto são os catetos. Eles são menores que a hipotenusa.

3. Teorema A altura relativa à hipotenusa de um triângulo retângulo determina dois outros triângulos retângulos, que são semelhantes ao primeiro.

4. Os triângulos são semelhantes Observando os triângulos ∆ABC, ∆HBA e ∆ HCA, podemos verificar que: ∆ ABC ~ ∆HBA (caso A.A.), pois os ângulos A e H são congruentes (retos) e o ângulo B é comum aos dois triângulos. Da mesma forma, podemos comparar os triângulos ∆ABC ~ ∆HCA, também semelhantes pelo caso A.A.

5. Relações Métricas A semelhança entre esses triângulos permite estabelecer importantes relações métricas no triângulo retângulo. 1) Da semelhança entre os triângulos ABC e HBA, temos: Da semelhança entre os triângulos ABC e HBA, temos:

6. Relações Métricas 2) Da semelhança entre os triângulos HBA e HCA, temos: 3) Da semelhança entre os triângulos ABC e HBA, temos:

7. Teorema de Pitágoras Considerando as relações e somando ambas membro a membro, temos:

8. Referências Bibliográficas 1) Bianchini, Edwaldo. Matemática. São Paulo. Editora Moderna. 8ª série. 1996. 2)http://pt.wikipedia.org/wiki/Tri%C3%A2ngulo_ret%C3%A2ngulo