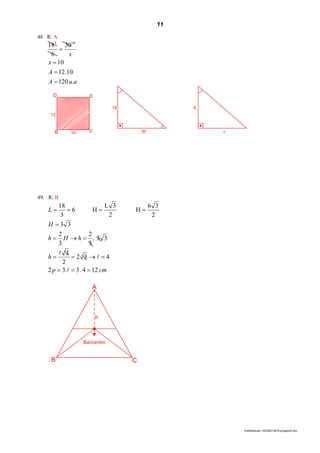
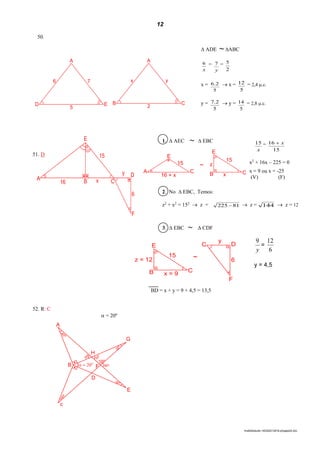
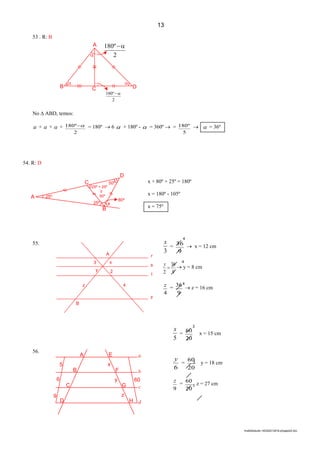
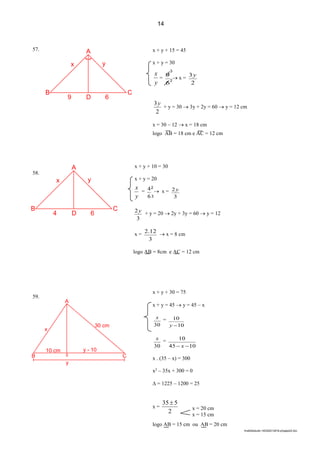
(a) O documento apresenta uma lista de exercícios de matemática com 32 questões sobre conjuntos numéricos, geometria plana e trigonometria. (b) As questões abordam tópicos como interseção e união de conjuntos, coordenadas de pontos no plano cartesiano, simetria, arcos trigonométricos e identidades trigonométricas. (c) Há também exercícios propostos envolvendo funções trigonométricas como seno, cosseno e tangente.

![2
lmat02estudo-140325212816-phpapp02.doc
11. (UESC – BA) O valor de x = 0,32121... – 1,32121... é:
a)0
b)
445
158
c)– 1
d)1
e)
990
318
12. (UESP) Dados os conjuntos A = 6x/Nx ,
B = 1x2/Zx e C = }0x2/Rx{ ,
então (B – A) C é:
a) {– 1, 0, 1}
b) {– 1, 0}
c) {– 2, – 1, 0}
d) [–1, 0[
e) ] –2, 0[
13. (Consultec) A solução da equação do 10
grau
1
2
3x
3
2x
, pertence ao conjunto:
a) Q Q’
b) Z*
– Z-
c) N
d) Z+
e) Z-
14. (Consultec) Dados os conjuntos A = {x R / x > 2} e
B = 4x/Rx , assinale a alternativa correta.
a) BA Ø
b) }4x2/Rx{BA
c) }4x2/Rx{BA
d) }3{BA
e) RBA
15. (Consultec) Certo dia, ao resolver a inequação
10
12
x1
4
5x2
, Astrogildo observou que sua
idade, em anos, era igual ao maior número inteiro que
a satisfazia. Quantos anos Astrogildo tinha nessa
ocasião?
a)27
b)25
c)31
d)22
e)19
OBS: Questões 17, 18 e 19 só serão consideradas
com justificativas.
16. (Consultec) Sejam A e B subconjuntos de
}.9x/Nx{V *
Se B = {1, 3, 4, 6}, BA {7, 8}
e BA {2, 3, 4, 5 7, 8}, determine a soma dos
elementos que pertencem ao conjunto A.
17. (UFBA) Considerando-se os conjuntos:
A = {x N / x < 4}
B = {x N / 2x + 3 = 7}
C = { x R / x2
+ 5x + 6 = 0},
é verdade que:
(01) ABA
(02) CA {2, 3}
(04) A – B = {0, 1, 3}
(08) RCA
(16) A)CB(
(32) (A – B) (B C) = Ø
18. Sobre conjuntos numéricos, podemos afirmar que:
01) a soma de dois irracionais é sempre um irracional.
(02) a soma de um inteiro com um fracionário
pode ser um inteiro.
(04) todo número racional é real.
(08) se x é real, os números da forma 5
x
1
também o é.
(16) o produto de inteiro por outro inteiro pode ser um
natural.
(32) 0,35 ... Q'.
(64) existem números irracionais que podem ser
colocados na forma m/n, com m Z e n Z*.
19. Sobre conjuntos numéricos, podemos afirmar que:
(01) 'Q
(02) ZxNx
(04) 'Qx/Qx
(08) Z*
Q
(16) QQ Ø
(32) 'Q255
20. Determine a qual quadrante pertencem os pontos a
seguir relacionados:
,2A ,
13
11
,7B , 3,6C e 13,3D ](https://image.slidesharecdn.com/lmat02estudo-140325212816-phpapp02/85/L-mat02-estudo-com-2-320.jpg)








![2
lmat02estudo-140325212816-phpapp02.doc
06. R: E
F = {-2, -1, 0, 1, 2}
|-2| = 2
|-1| = 1
|0| = 0 Logo: {xZ /-2 x 2}
|2| = 2
|-1| = 1
07. R: E
A = (NZ) Q = NQ = Q
N = N (ZQ) = NZ = Z
AN = Z Q = Z
08. R: C
a)QN = Q R (V)
b)QN = N R (V)
c)QN = Q logo não é R (F)
d)QR = Q (V)
e)QR = Q, logo (V)
09. R: C
CR = R
Q (N Z ) = QN = Q
(ZQ) N = Z N = Z
RQZ = Z
10. R: E
1 2 5 6
A
B
A B
11. R: C
0, 32121... =
990
318
990
3321
0, 32121... -1 + 0, 32121... = -1
12. R: E
A = {0, 1, 2, 3, 4 ,5, 6}
B = {-1, 0, 1}
C = ] -2, 0 [
B – A = {-1}
B – AC = {-1}] -2, 0 [ = ] -2, 0[](https://image.slidesharecdn.com/lmat02estudo-140325212816-phpapp02/85/L-mat02-estudo-com-11-320.jpg)