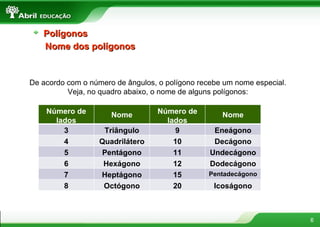
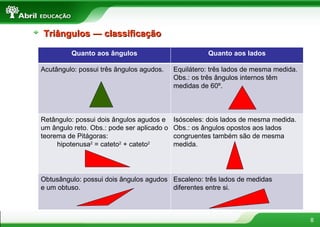
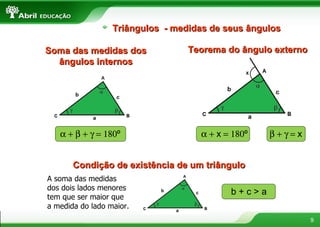
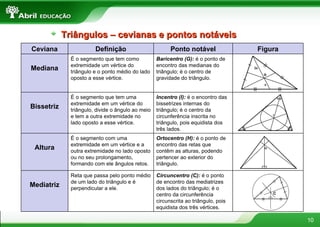
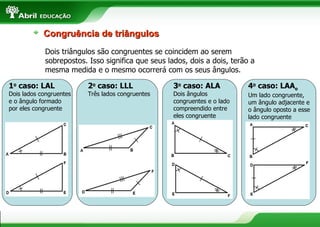
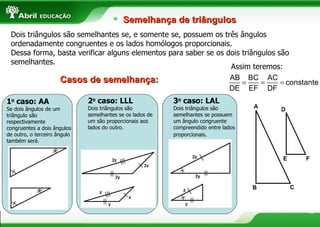
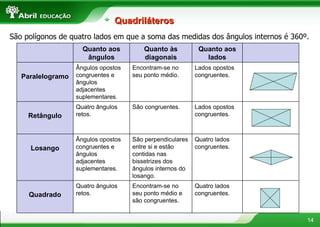
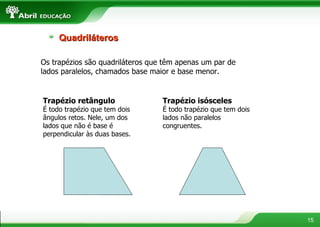
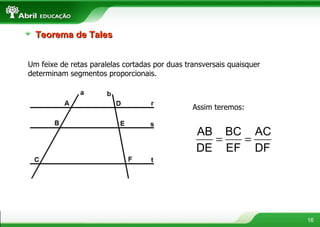
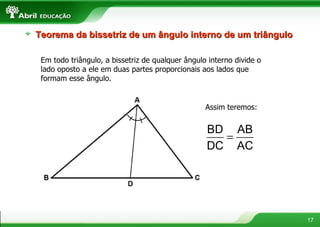
O documento fornece definições e propriedades de polígonos, triângulos, quadriláteros e teoremas geométricos. Aborda conceitos como polígonos convexos e côncavos, elementos de um polígono, polígonos regulares, classificação de triângulos, congruência e semelhança de triângulos, relações métricas no triângulo retângulo, tipos de quadriláteros e teoremas de Tales e da bissetriz.

1. Geometria plana Índice Esquadros de madeira ― www.ser.com.br Polígonos Semelhança de triângulos Triângulos Congruência de triângulos Quadriláteros Teorema de Tales Teorema da bissetriz de um ângulo interno de um triângulo Relações métricas no triângulo retângulo

2. Definição Chama-se polígono toda linha poligonal fechada simples juntamente com os pontos da região interna que essa linha determina. As figuras a seguir são polígonos As figuras a seguir não são polígonos Polígonos

3. Um polígono se diz convexo quando o segmento de reta que une dois pontos quaisquer de sua região interna está sempre contido nela. Polígonos convexos e polígonos côncavos Polígonos convexos Polígonos côncavos Um polígono se diz côncavo quando existem dois pontos de sua região interna tais que o segmento de reta por eles determinado não está contido nela. A B A B São polígonos convexos São polígonos côncavos Polígonos

4. Elementos de um polígono No polígono ABCDE ao lado temos que: A B C D E Os segmentos são os lados do polígono; Os pontos A, B, C, D, E são os vértices do polígono; Os segmentos são as diagonais do polígono; são os ângulos do polígono; Nota: Diagonal de um polígono é o segmento de reta que une dois vértices não consecutivos desse polígono. Polígonos

5. Polígonos regulares A B C D E Num polígono regular destacamos: O centro É o ponto que dista igualmente de todos os vértices do polígono. (Na figura ao lado é o ponto O .) M Polígonos Chama-se polígono regular a todo polígono que tem todos os lados congruentes e todos os ângulos congruentes (ângulos que possuem a mesma medida). O

6. Nome dos polígonos De acordo com o número de ângulos, o polígono recebe um nome especial. Veja, no quadro abaixo, o nome de alguns polígonos: Número de lados Nome Número de lados Nome 3 Triângulo 9 Eneágono 4 Quadrilátero 10 Decágono 5 Pentágono 11 Undecágono 6 Hexágono 12 Dodecágono 7 Heptágono 15 Pentadecágono 8 Octógono 20 Icoságono Polígonos

7. Polígonos Soma das medidas dos ângulos internos: Soma das medidas dos ângulos externos: Ângulos internos de um polígono regular: Ângulos externos de um polígono regular: Número de diagonais de um polígono:

8. Triângulos ― classificação Quanto aos ângulos Quanto aos lados Acutângulo: possui três ângulos agudos. Equilátero: três lados de mesma medida. Obs.: os três ângulos internos têm medidas de 60º. Retângulo: possui dois ângulos agudos e um ângulo reto. Obs.: pode ser aplicado o teorema de Pitágoras: hipotenusa 2 = cateto 2 + cateto 2 Isósceles: dois lados de mesma medida. Obs.: os ângulos opostos aos lados congruentes também são de mesma medida. Obtusângulo: possui dois ângulos agudos e um obtuso. Escaleno: três lados de medidas diferentes entre si.

9. Soma das medidas dos ângulos internos Teorema do ângulo externo Condição de existência de um triângulo A soma das medidas dos dois lados menores tem que ser maior que a medida do lado maior. Triângulos - medidas de seus ângulos  º  x  º  x b + c > a

10. Triângulos – cevianas e pontos notáveis Ceviana Definição Ponto notável Figura Mediana É o segmento que tem como extremidade um vértice do triângulo e o ponto médio do lado oposto a esse vértice. Baricentro (G): é o ponto de encontro das medianas do triângulo; é o centro de gravidade do triângulo. Bissetriz É o segmento que tem uma extremidade em um vértice do triângulo, divide o ângulo ao meio e tem a outra extremidade no lado oposto a esse vértice. Incentro (I): é o encontro das bissetrizes internas do triângulo; é o centro da circunferência inscrita no triângulo, pois equidista dos três lados. Altura É o segmento com uma extremidade em um vértice e a outra extremidade no lado oposto ou no seu prolongamento, formando com ele ângulos retos. Ortocentro (H): é o ponto de encontro das retas que contêm as alturas, podendo pertencer ao exterior do triângulo. Mediatriz Reta que passa pelo ponto médio de um lado do triângulo e é perpendicular a ele. Circuncentro (C): é o ponto de encontro das mediatrizes dos lados do triângulo; é o centro da circunferência circunscrita ao triângulo, pois equidista dos três vértices.

11. Dois triângulos são congruentes se coincidem ao serem sobrepostos. Isso significa que seus lados, dois a dois, terão a mesma medida e o mesmo ocorrerá com os seus ângulos. Congruência de triângulos 1 o caso: LAL Dois lados congruentes e o ângulo formado por eles congruente 3 o caso: ALA Dois ângulos congruentes e o lado compreendido entre eles congruente 4 o caso: LAA o Um lado congruente, um ângulo adjacente e o ângulo oposto a esse lado congruente 2 o caso: LLL Três lados congruentes

12. Dois triângulos são semelhantes se, e somente se, possuem os três ângulos ordenadamente congruentes e os lados homólogos proporcionais. Dessa forma, basta verificar alguns elementos para saber se os dois triângulos são semelhantes. Casos de semelhança: Assim teremos: Semelhança de triângulos 1 o caso: AA Se dois ângulos de um triângulo são respectivamente congruentes a dois ângulos de outro, o terceiro ângulo também será. 3 o caso: LAL Dois triângulos são semelhantes se possuem um ângulo congruente compreendido entre lados proporcionais . 2 o caso: LLL Dois triângulos são semelhantes se os lados de um são proporcionais aos lados do outro.

13. Definições dos segmentos: Assim teremos: Relações métricas no triângulo retângulo Considere um triângulo ABC , retângulo em A , e o segmento perpendicular ao lado , com D em .

14. São polígonos de quatro lados em que a soma das medidas dos ângulos internos é 360º. Quadriláteros Quanto aos ângulos Quanto às diagonais Quanto aos lados Paralelogramo Ângulos opostos congruentes e ângulos adjacentes suplementares. Encontram-se no seu ponto médio. Lados opostos congruentes. Retângulo Quatro ângulos retos. São congruentes. Lados opostos congruentes. Losango Ângulos opostos congruentes e ângulos adjacentes suplementares. São perpendiculares entre si e estão contidas nas bissetrizes dos ângulos internos do losango. Quatro lados congruentes. Quadrado Quatro ângulos retos. Encontram-se no seu ponto médio e são congruentes. Quatro lados congruentes.

15. Os trapézios são quadriláteros que têm apenas um par de lados paralelos, chamados base maior e base menor. Trapézio retângulo É todo trapézio que tem dois ângulos retos. Nele, um dos lados que não é base é perpendicular às duas bases. Trapézio isósceles É todo trapézio que tem dois lados não paralelos congruentes. Quadriláteros

16. Um feixe de retas paralelas cortadas por duas transversais quaisquer determinam segmentos proporcionais. Assim teremos: Teorema de Tales

17. Em todo triângulo, a bissetriz de qualquer ângulo interno divide o lado oposto a ele em duas partes proporcionais aos lados que formam esse ângulo. Assim teremos: Teorema da bissetriz de um ângulo interno de um triângulo