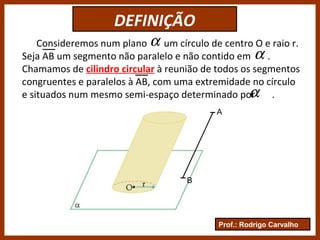
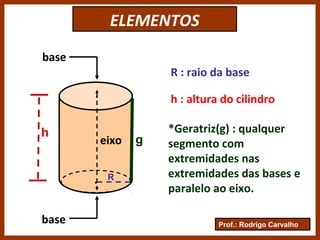
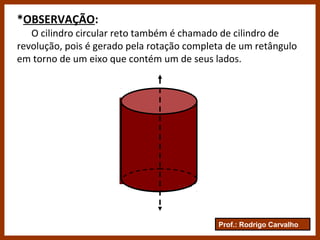
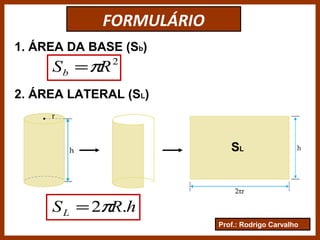
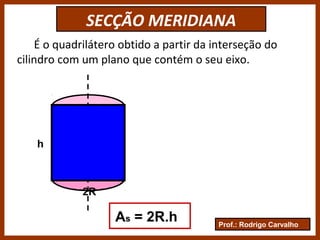
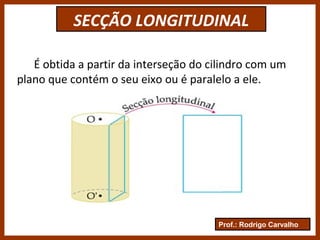
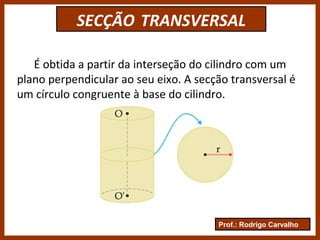
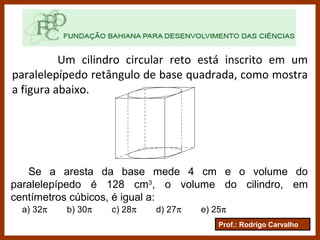
O documento define e classifica os cilindros circulares, descrevendo suas partes e elementos. Apresenta fórmulas para calcular a área da base, área lateral, área total e volume de um cilindro circular. Exemplifica como calcular a altura de um cilindro a partir da igualdade entre sua área lateral e a área da base.

1. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho

2. Prof.: Rodrigo Carvalho
DEFINIÇÃO
Consideremos num plano um círculo de centro O e raio r.
Seja AB um segmento não paralelo e não contido em .
Chamamos de cilindro circular à reunião de todos os segmentos
congruentes e paralelos à AB, com uma extremidade no círculo
e situados num mesmo semi-espaço determinado por .
α
α
α
A
B

3. Prof.: Rodrigo Carvalho
ELEMENTOS
base
base
.
.
R
R : raio da base
h
h : altura do cilindro
eixo
*Geratriz(g) : qualquer
segmento com
extremidades nas
extremidades das bases e
paralelo ao eixo.
g

4. Prof.: Rodrigo Carvalho
CLASSIFICAÇÃO
CILINDRO CIRCULAR
OBLÍQUO
CILINDRO CIRCULAR
RETO
As geratrizes são
oblíquas aos planos
das bases.
As geratrizes são
perpendiculares aos
planos das bases.

5. Prof.: Rodrigo Carvalho
*OBSERVAÇÃO:
O cilindro circular reto também é chamado de cilindro de
revolução, pois é gerado pela rotação completa de um retângulo
em torno de um eixo que contém um de seus lados.

6. Prof.: Rodrigo Carvalho
FORMULÁRIO
1. ÁREA DA BASE (Sb)
2. ÁREA LATERAL (SL)
2
RSb π=
SL
hRSL .2π=

7. Prof.: Rodrigo Carvalho
3. ÁREA TOTAL (St)
É a soma das áreas das bases com a área lateral.
Lbt SSS += .2
hRRSt .2.2 2
ππ +=
)(2 hRRSt += π

8. Prof.: Rodrigo Carvalho
4. VOLUME (V)
É o produto da área da base pela altura do cilindro.
hSV b .=
hRV .2
π=
Exemplo1: A área lateral de um cilindro de revolução de
10 cm de raio é igual à área da base. Calcule a altura
desse cilindro.

9. Prof.: Rodrigo Carvalho
(2010)

10. Prof.: Rodrigo Carvalho
SECÇÃO MERIDIANA
É o quadrilátero obtido a partir da interseção do
cilindro com um plano que contém o seu eixo.
2R
h As
As = 2R.h

11. Prof.: Rodrigo Carvalho
Se a secção meridiana de um cilindro é um quadrado,
então o cilindro é denominado CILINDRO EQUILÁTERO.
*OBSERVAÇÃO:
2R
h h = 2R
Exemplo2: A área da secção meridiana de um cilindro
equilátero é igual a 36 cm . Determine o volume desse
sólido.
2

12. Prof.: Rodrigo Carvalho
SECÇÃO LONGITUDINAL
É obtida a partir da interseção do cilindro com um
plano que contém o seu eixo ou é paralelo a ele.

13. Prof.: Rodrigo Carvalho
SECÇÃO TRANSVERSAL
É obtida a partir da interseção do cilindro com um
plano perpendicular ao seu eixo. A secção transversal é
um círculo congruente à base do cilindro.

14. Prof.: Rodrigo Carvalho
EXERCÍCIOS:
01. Duas latas A e B, em forma de um cilindro circular
reto, têm a mesma altura. Sabendo-se que o raio da
base de A é o dobro do raio da base de B, pode-se
afirmar que:
a) A e B têm a mesma capacidade;
b) a capacidade de B é 25% da capacidade de A;
c) a capacidade de A é 20% da capacidade de B;
d) a capacidade de A é 25% da capacidade de B;
e) a razão entre a capacidade de A e a capacidade de B é 2.

15. Prof.: Rodrigo Carvalho
Um cilindro circular reto está inscrito em um
paralelepípedo retângulo de base quadrada, como mostra
a figura abaixo.
Se a aresta da base mede 4 cm e o volume do
paralelepípedo é 128 cm3
, o volume do cilindro, em
centímetros cúbicos, é igual a:
a) 32π b) 30π c) 28π d) 27π e) 25π

16. Prof.: Rodrigo Carvalho
Sugestão de exercícios:
LIVRO 3 - CAPÍTULO 5
Questões: 163, 166, 168, 173, 174 e 176.