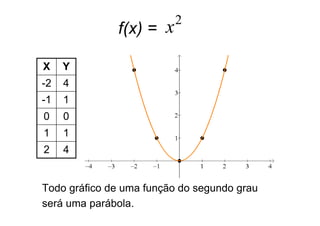
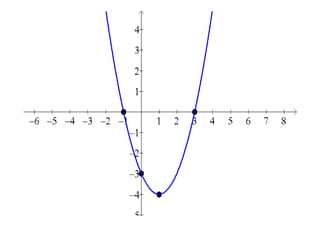
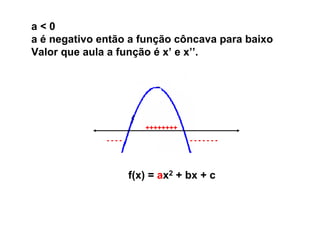
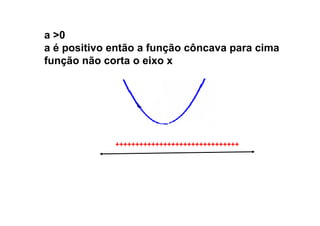
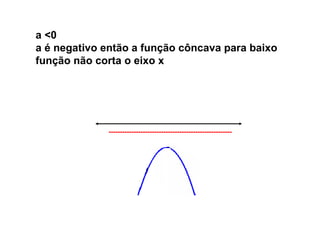
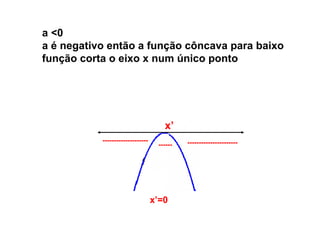
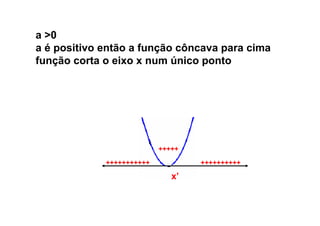
Este documento descreve as funções quadráticas, incluindo: 1) Como plotar o gráfico de uma função quadrática e interpretar os valores das constantes a, b e c; 2) Como encontrar as raízes e o vértice de uma função quadrática; 3) Como determinar os pontos onde a função corta os eixos x e y.

1. Colégio Juvenal de Carvalho
Matemática- Profa: Jacqueline
Função Quadrática
Fonte pesquisa : www.cdb.br/prof/arquivos/ Prof. Dejahyr-2009

2. 2
f(x) = x
X Y
-2 4
-1 1
0 0
1 1
2 4
Todo gráfico de uma função do segundo grau
será uma parábola.

3. Valores das constantes
a > 0 → concavidade para cima
a < 0 → concavidade para baixo

c → valor que toca no eixo y

∆ < 0 → não toca no eixo x
∆ > 0 → toca em dois pontos no eixo x

∆ = 0 → toca em um ponto no eixo x

4. Zero da Função do Segundo Grau
É o valor que anula a função f(x), isto é,
f(x)=0
ax2+bx+c = 0

5. f(x) = x − 2 x −
2
3
• Achar as raízes da
função
x′ = −1 x′′ = 3
• O valor de c toca o
−(−2) 2
eixo do y XV = = =1
2.1 2
• Achar o vértice da −(16) −16
função YV = = = −4
4.1 4
 −b −∆ 
V = ,  V = (1, −4)
 2a 4a 

7. Ponto onde a função corta o eixo x
Basta fazer y = 0, na função
f(x)= ax2 + bx + c, para y = 0
ax2 + bx + c =0
Ponto onde corta o eixo y:
O valor de c toca o eixo do y

8. ESTUDO DO SINAL
a >0
a é positivo então a função côncava para cima
Valor que anula a função é x’ e x’’.
++++++++ ++++++++
------
f(x) = ax2 + bx + c

9. a<0
a é negativo então a função côncava para baixo
Valor que aula a função é x’ e x’’.
++++++++
---- -------
f(x) = ax2 + bx + c

10. a >0
a é positivo então a função côncava para cima
função não corta o eixo x
+++++++++++++++++++++++++++++++

11. a <0
a é negativo então a função côncava para baixo
função não corta o eixo x
------------------------------------------------------

12. a <0
a é negativo então a função côncava para baixo
função corta o eixo x num único ponto
x’
-------------------- ----------------------
------
x’=0

13. a >0
a é positivo então a função côncava para cima
função corta o eixo x num único ponto
+++++
+++++++++++ ++++++++++
x’

14. GRÁFICO DA FUNÇÃO
f(x) = x2 – 2x - 3 • Ponto onde corta o eixo x
é: (-1,0)e(3,0)
• Ponto onde corta o eixo y
é: (0,-3)
• vértice (1,-4)