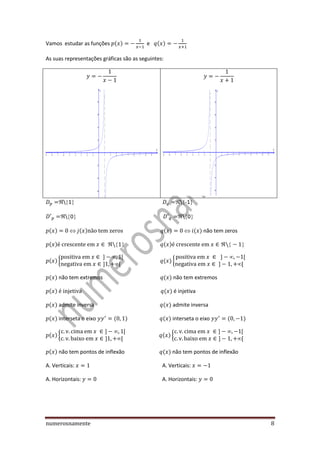
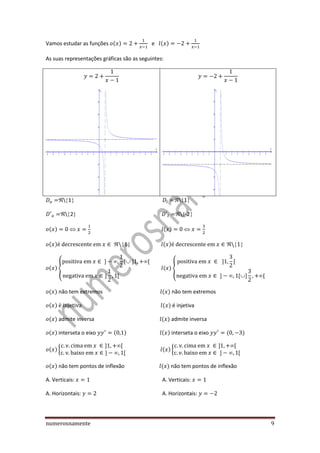
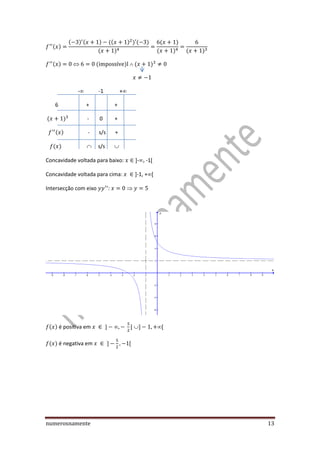
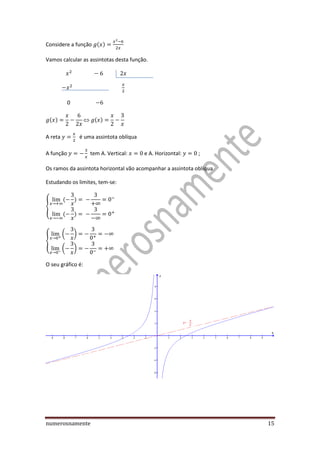
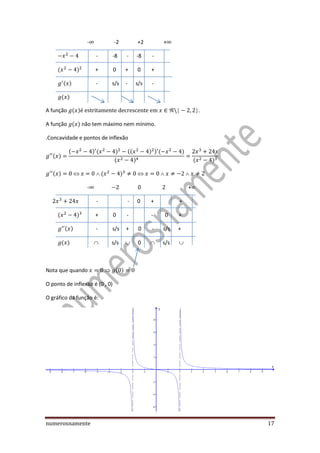
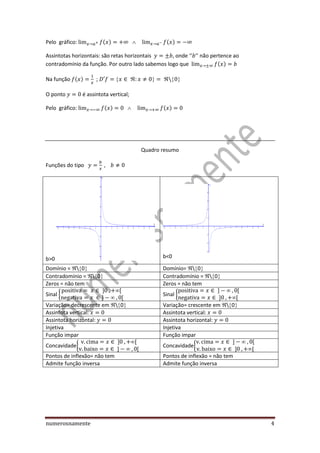
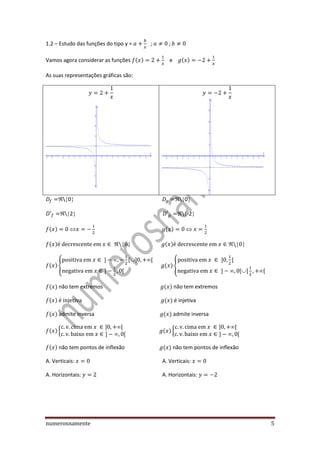
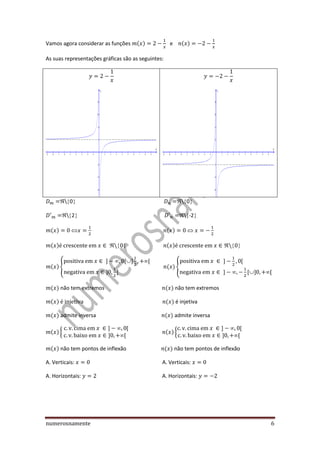
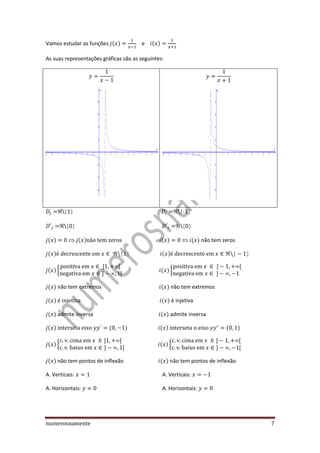
1) O documento apresenta um estudo detalhado de funções reais de variável real, incluindo o conceito de domínio, contradomínio, zeros, paridade, sinal, variação, extremos, concavidade e pontos de inflexão, assintotas e casos particulares. 2) É feito um estudo comparativo das funções do tipo f(x)=x^n, analisando suas propriedades gráficas e algébricas. 3) O documento conclui com notas sobre o conceito de assintotas em fun

1. numerosnamente 1
Estudo de funções
1.1 Estudo da função real de variável real: ( )
O seu gráfico:
a)- O domínio de ( )
b)- O contradomínio de ( ) domínio da função inversa; pelo gráfico vê-se que:
( )
c)- Zeros ou raízes da função:
Basta igualar a zero a função para determinar os seus zeros. Assim:
( ) .
d)- Uma função admite inversa se for injetiva, ou seja:
 ( ) ( )
Pelo gráfico vê-se que a função ( ) é injetiva, pois a cada objeto corresponde uma e só
uma imagem .
e)- A sua função inversa é: , então: ( )
f)-Paridade da função:
Uma função é par se ( ) ( )
Uma função é impar se ( ) ( )
Na função ( ) , calculando ( )
( )
; ( )
Assim a função ( ) é uma função impar, .

2. numerosnamente 2
g)- Sinal e variação
Para calcular o sinal, pode ver-se graficamente onde a função é positiva ou onde é negativa.
Para a função ( ) , tem-se:
A função é positiva para
A função é negativa para
O sinal da função também pode ser calculado através da 1ª derivada da função e fazer o seu
estudo. Neste caso teremos:
( )
( ) ( )
( ) o numerador não tem zero e o zero do denominador é , mas
tem-se de ter em atenção que o zero não pertence ao domínio da função, por isso quando se
faz o estudo nesse ponto ira ser sem significado:
-1 - -
+ 0 +
( ) - s/s -
( ) s/s
Pela análise da tabela, tem-se que:
A função é decrescente em 
 ( ) ( )  a função é decrescente
 ( ) ( )  a função é crescente
h) Extremos relativos e absolutos
São os pontos máximos e mínimos que uma função pode ter. Estes pontos tem de pertencer
ao domínio da função.
Na função ( ) ,não tem extremos, pois o ponto não pertence ao domínio da
função.
i)- Concavidade e pontos de inflexão
Esta informação pode ser obtida do gráfico de ( )

3. numerosnamente 3
Concavidade voltada para cima em
Concavidade voltada para baixo em
Os possíveis pontos de inflexão são os pontos onde há mudança do sentido da concavidade, e
têm de pertencer ao domínio da função.
Na função ( ) , não há pontos de inflexão, apesar de haver mudança no sentido da
concavidade, pois o ponto não pertence ao domínio da função .
Também podemos obter as concavidades e pontos de inflexão, através do estudo da 2ª
derivada da função .
Temos então:
( ) ; ( )
( )
( ) ( ) ( ) ( )
( ) ; o numerador não tem raízes. A raiz do denominador é , mas
temos de ter em atenção que não pertence ao domínio, logo nesse ponto é sem
significado o estudo da 2ª derivada. Tem-se:
2 + +
- 0 +
( ) - s/s +
( )  s/s 
Pela análise da tabela, tem-se:
Concavidade voltada para cima em
Concavidade voltada para baixo em
Ponto de inflexão não tem apesar de haver mudança no sentido da concavidade, pois
não pertence ao domínio de .
j) Assintotas
Assintotas verticais: são as retas verticais , onde “ ’’ não pertence ao domínio da
função. Por outro lado sabemos logo que ( )
Na função ( ) ;
O ponto é uma assintota vertical;

4. numerosnamente 4
Pelo gráfico: ( ) ( )
Assintotas horizontais: são retas horizontais , onde ‘’ ’’ não pertence ao
contradomínio da função. Por outro lado sabemos logo que ( )
Na função ( ) ;
O ponto é assintota vertical;
Pelo gráfico: ( ) ( )
Quadro resumo
Funções do tipo
b>0 b<0
Domínio = 0 Domínio= 0
Contradomínio = 0 Contradomínio = 0
Zeros = não tem Zeros = não tem
Sinal { Sinal {
Variação= decrescente em 0 Variação= crescente em 0
Assintota vertical: Assintota vertical:
Assintota horizontal: Assintota horizontal:
Injetiva Injetiva
Função impar Função impar
Concavidade{ Concavidade{
Pontos de inflexão= não tem Pontos de inflexão = não tem
Admite função inversa Admite função inversa

5. numerosnamente 5
1.2 – Estudo das funções do tipo y = ;
Vamos agora considerar as funções ( ) e ( )
As suas representações gráficas são:
0 0
2 -2
( ) ( )
( ) ( )
( ) {

( ) {

( ) não tem extremos ( ) não tem extremos
( ) ( ) é injetiva
( ) admite inversa ( ) admite inversa
( ) { ( ) {
( ) não tem pontos de inflexão ( ) não tem pontos de inflexão
A. Verticais: A. Verticais:
A. Horizontais: A. Horizontais:

6. numerosnamente 6
Vamos agora considerar as funções ( ) e ( )
As suas representações gráficas são as seguintes:
0 0
2 -2
( ) ( )
( ) ( )
( ) {

( ) {

( ) não tem extremos ( ) não tem extremos
( ) ( ) é injetiva
( ) admite inversa ( ) admite inversa
( ) { ( ) {
( ) não tem pontos de inflexão ( ) não tem pontos de inflexão
A. Verticais: A. Verticais:
A. Horizontais: A. Horizontais:

7. numerosnamente 7
Vamos estudar as funções ( ) e ( )
As suas representações gráficas são as seguintes:
1 -1
0 0
( ) ( ) ( ) ( ) não tem zeros
( ) ( )
( ) { ( ) {
( ) não tem extremos ( ) não tem extremos
( ) ( ) é injetiva
( ) admite inversa ( ) admite inversa
( ) ( ) ( ) ( )
( ) { ( ) {
( ) não tem pontos de inflexão ( ) não tem pontos de inflexão
A. Verticais: A. Verticais:
A. Horizontais: A. Horizontais:

8. numerosnamente 8
Vamos estudar as funções ( ) e ( )
As suas representações gráficas são as seguintes:
1 -1
0 0
( ) ( ) ( ) ( ) não tem zeros
( ) ( )
( ) { ( ) {
( ) não tem extremos ( ) não tem extremos
( ) ( ) é injetiva
( ) admite inversa ( ) admite inversa
( ) interseta o eixo ( ) ( ) interseta o eixo ( )
( ) { ( ) {
( ) não tem pontos de inflexão ( ) não tem pontos de inflexão
A. Verticais: A. Verticais:
A. Horizontais: A. Horizontais:

9. numerosnamente 9
Vamos estudar as funções ( ) e ( )
As suas representações gráficas são as seguintes:
1 1
2 -2
( ) ( )
( ) ( )
( ) {

( ) {

( ) não tem extremos ( ) não tem extremos
( ) ( ) é injetiva
( ) admite inversa ( ) admite inversa
( ) interseta o eixo ( ) ( ) interseta o eixo ( )
( ) { ( ) {
( ) não tem pontos de inflexão ( ) não tem pontos de inflexão
A. Verticais: A. Verticais:
A. Horizontais: A. Horizontais:

10. numerosnamente 10
Vamos estudar as funções ( ) e ( )
As suas representações gráficas são as seguintes:
-1 -1
2 -2
( ) ( )
( ) ( )
( ) {

( ) {

( ) não tem extremos ( ) não tem extremos
( ) ( ) é injetiva
( ) interseta o eixo ( ) ( ) interseta o eixo ( )
( ) admite inversa ( ) admite inversa
( ) { ( ) {
( ) não tem pontos de inflexão ( ) não tem pontos de inflexão
A. Verticais: A. Verticais:
A. Horizontais: A. Horizontais:

11. numerosnamente 11
Vamos estudar as funções ( ) e ( )
As suas representações gráficas são as seguintes:
1 -1
2 -2
( ) ( )
( ) ( )
( ) {

( ) {

( ) não tem extremos ( ) não tem extremos
( ) ( ) é injetiva
( ) interseta o eixo ( ) ( ) interseta o eixo ( )
( ) admite inversa ( ) admite inversa
( ) { ( ) {
( ) não tem pontos de inflexão ( ) não tem pontos de inflexão
A. Verticais: A. Verticais:
A. Horizontais: A. Horizontais:

12. numerosnamente 12
1.3 – Estudo das funções do tipo , ;
Vamos estudar a função ( )
Aplicando o algoritmo da divisão, tem-se:
2
( )
( )
( )
( )
( )
Variação e extremos: ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
( ) ( )
( ) ( ) ( )
- -1 +
-3 - -
( ) + 0 +
( ) - s/s -
( ) s/s
Variação: Estritamente monótona decrescente em -1
( ) não tem extremos.
Concavidades e pontos de inflexão: ( )

13. numerosnamente 13
( )
( ) ( ) (( ) ) ( )
( )
( )
( ) ( )
( ) ( ) ( )
- -1 +
6 + +
( ) - 0 +
( ) - s/s +
( )  s/s 
Concavidade voltada para baixo: - , -1
Concavidade voltada para cima: -1, +
Intersecção com eixo ’: 
( ) é positiva em 
( ) é negativa em

14. numerosnamente 14
Assintotas Oblíquas
Funções do tipo ,
Sempre que o expoente da variável do numerador é maior que o expoente da variável do
denominador, temos de aplicar o algoritmo da divisão de polinómios e fica determinada a
assintota oblíqua.
Considere a função ( )
4
( )
Assim a reta é a assintota oblíqua
A função tem como A. Vertical: e como A. Horizontal:
Estudando os limites, tem-se:
{
( )
( )
{
( )
( )
O seu gráfico é:

15. numerosnamente 15
Considere a função ( )
Vamos calcular as assintotas desta função.
0
( ) ( )
A reta é uma assintota oblíqua
A função tem A. Vertical: e A. Horizontal: ;
Os ramos da assintota horizontal vão acompanhar a assintota oblíqua
Estudando os limites, tem-se:
{
( )
( )
{
( )
( )
O seu gráfico é:

16. numerosnamente 16
Caso particular em estudo:
Considere a função ( ) . Faça o estudo completo da função:
Resolução:
( )
é o domínio da função inversa, mas a função não é injetiva:
( ) ; ( )
( ) ( ) ( ) ( )
( )( )
A função é não injetiva, logo não admite inversa e o seu contradomínio é
.Zeros  ( )
.Paridade
( )
( )
( )
( )
Logo ( ) ( ) a função é impar
.Sinal e variação
( )
( ) ( ) ( ) ( )
( )
( ) ( )
( ) ( )
( )
C.A: √ ( ( ))
(estes pontos não pertencem ao domínio, logo na tabela em
estudo serão sem significado)

17. numerosnamente 17
- -2 +2 +
- -8 - -8 -
( ) + 0 + 0 +
( ) - s/s - s/s -
( )
A função ( ) .
A função ( ) não tem máximo nem mínimo.
.Concavidade e pontos de inflexão
( )
( ) ( ) (( ) ) ( )
( ) ( )
( ) ( )
- 0 +
- - 0 + +
( ) + 0 - - 0 +
( ) - s/s + 0 - s/s +
( )  s/s  0  s/s 
Nota que quando  ( )
O ponto de inflexão é (0 , 0)
O gráfico da função é:

18. numerosnamente 18
Notas a reter sobre assintotas
. Se tivermos uma função ( )
0 ; 0
Assintotas verticais:
Assintotas horizontais:
.Se tivermos uma função ( )
0 ; a
Assintotas verticais:
Assintotas horizontais:
.Se tivermos uma função ( )
c ; 0
Assintotas verticais:
Assintotas horizontais:
.Se tivermos uma função ( )
c ; a
Assintotas verticais:
Assintotas horizontais:
.Se tivermos uma função ( )
c ; 0
Assintotas verticais:
Assintotas horizontais:
Assintotas oblíquas: