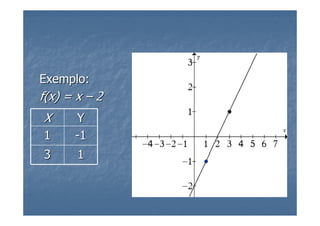
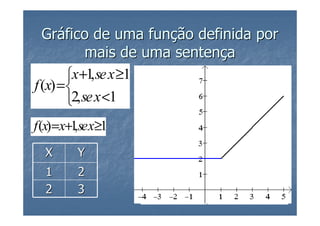
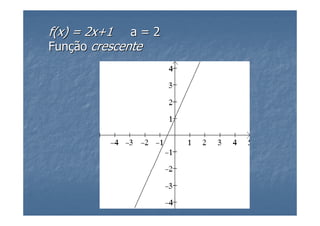
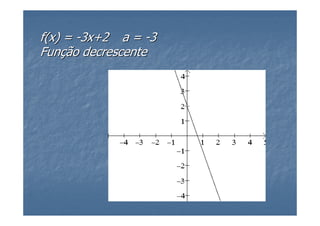
1) O documento apresenta conceitos fundamentais sobre operações com intervalos, funções polinomiais do primeiro grau e suas características. 2) São descritas as operações de união, intersecção e diferença entre intervalos, bem como exemplos ilustrativos. 3) As funções polinomiais do primeiro grau, também chamadas de funções afins, são definidas e exemplificadas, mostrando casos especiais e como representá-las graficamente.

1. Colégio Juvenal de Carvalho
Matemática- Profa: Jacqueline
Operações com intervalos

2. 1º) União de Intervalos: (a, b) ∪ (c, d) = (a, d)
a b
c d
a d
Exemplo: [4, 9] ∪ [6, 12] = [ 4, 12]
4 6 9 12
Por descrição: {x ∈ℜ 4 ≤ x ≤ 12}

3. 2º) Intersecção de Intervalos:
(a, b) ∩ (c, d) = (c, b)
a b
c d
c b
Exemplo: [4, 9] ∩ [6, 12] = [ 6, 9 ]
4 6 9 12
Por notação: [ 6, 9 ]

4. 3º) Diferença de Intervalos:
(a, b) − (c, d) = (a, c)
a b
c d
a c
Exemplo: [4, 9] − [6, 12] = [ 4, 6 ]
4 6 9 12

5. Colégio Juvenal de Carvalho
Matemática- Profa: Jacqueline
Funções Polinomiais do
1º Grau
(Função Afim)

6. Definição
Toda função polinomial da forma
f(x) = ax + b,
a≠0
com , é dita função do 1° grau.
Ex.: f(x) = 3x – 2; a = 3 e b = - 2
f(x) = - x + ½; a = -1 e b = ½
f(x) = -2x; a = -2 e b = 0

7. Casos Especiais
Função linear b = 0, f(x) = 3x
Função Identidade b = 0 e a = 1, ou
seja, f(x) = x
Função constante a = 0, f(x) = 3

8. Exercícios resolvidos
1°) Dada a função f(x) = ax + 2, determine o
valor de a para que se tenha f(4)=20.
f ( 4 ) = a .4 + 2, co m o f ( 4 ) = 2 0, en tã o
4a + 2 = 20
4a = 18
18
a =
4
9
a =
2

9. 2°) Dada a função f(x) = ax + b, com a
diferente de zero, sendo f(3) = 5 e
f(-2) = - 5, calcule f(1/2).
f(3)=5: a.3 + b =5
f(-2) = - 5: a.(-2) + b = -5
3a + b = 5

 −2 a + b = −5

10. Existem dois métodos para resolver esse
sistema: ADIÇÃO E SUBSTITUIÇÃO
1° ADIÇÃO: Multiplicar a primeira equação
por (-1) e somar as equações
 −3a − b = −5 −2a + b = −5

−2a + b = −5 − 2 .2 + b = − 5
−5a = −10 b = −5 + 4
a = 2 b = −1

11. 2° SUBSTITUIÇÃO: Escolhe uma equação
isolando uma letra e depois substitui essa
letra isolada na equação que sobrou
3a + b = 5

−2a + b = −5
3a + b = 5 − 2a + b = −5
b = 5 − 3a − 2 a + (5 − 3 a ) = − 5
− 5a = −5 − 5
b = 5 − 3.2 a=2
b = −1

12. Logo, a função é f(x)= 2x – 1.
Assim,
f(1/2)=2.(1/2) - 1 = 1 – 1
f(1/2) = 0

13. Há uma outra forma de resolver esse tipo
de exercício que se conhece os valores de
uma função em dois pontos distintos.
Basta usar a fórmula:
y2 − y1
a= , x1 ≠ x2
x2 − x1
y1 x2 − y2 x1
b= , x1 ≠ x2
x2 − x1

14. Voltando a questão, quem seria esses
valores?
Temos que f(3) = 5 e f(-2) = - 5
Então, x1 = 3, y1 = 5
x2 = −2, y2 = −5
Logo,
−5 − 5 −10
a= = =2
−2 − 3 −5
5.(−2) − (−5).3 −10 +15 5
b= = = = −1
−2 − 3 −5 −5

15. Gráficos
Toda gráfico de uma função do 1° grau é
uma reta.
Estudaremos como essa reta vai se
comportar através de cada função.

16. Como fazer um gráfico
1° método:
Para achar o gráfico de qualquer função,
basta achar dois pontos qualquer dela e
passar uma reta entre essas retas.

17. Exemplo:
f(x) = x – 2
X Y
1 -1
3 1

18. 2° método:
1° passo: iguale a função a zero. O valor de
x que você achar é que passará no eixo do
x.
2° passo: o valor de b é o ponto que toca
no eixo do y.

19. x–2=0
x=2
b=-2

20. Gráfico de uma função definida por
mais de uma sentença
x+1, se x ≥1
f (x) = 
2, se x <1
f (x) =x+1sex≥1
,
X Y
1 2
2 3

21. Crescimento de decrescimento de
uma função
Uma função será crescente quando a>0
Uma função será decrescente quando a<0

22. f(x) = 2x+1 a = 2
Função crescente

23. f(x) = -3x+2 a = -3
Função decrescente

24. EXERCÍCIOS
Igualdade entre pares ordenados:
Dois pares ordenados são iguais quando
seus elementos forem iguais.
Notação: (x, y) = ( a, b) ⇒ x = a e y = b
Segundo essa afirmação, calcule as variáveis
nas igualdades entre os pares dados:
a) ( 2a + b, 5a – 3b) = (3, 2)
b) (a + 2b, 17) = (6, a + b)
c) (a2 + a, 4b2 – 1 ) = ( 2, 7)

25. Operações com intervalos:
A = [-6, 0] , B = [-2, 4] e C = [-3, 2]
Calcule e represente por descrição , notação
e na reta real.
a)A ∪ B = b) A ∩ C = c) B − C =
d) C − A =