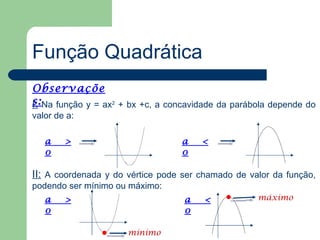
Este documento descreve como construir o gráfico de uma função quadrática a partir de seus pontos-chave: (1) zeros, onde o gráfico corta o eixo x; (2) vértice, o ponto mais alto ou baixo; (3) termo independente, onde corta o eixo y. Ele exemplifica como calcular esses pontos para f(x)=x^2-2x-3 e f(x)=-x^2+2x+8, e observa que a concavidade depende do sinal de a e que nem sempre há dois zeros reais.

1. Função Quadrática – Parte III
Ângelo Moreira dos Reis

2. Função Quadrática
Gráfico da Função Quadrática
 Toda Função Quadrática, do tipo f ( x) = ax 2 + bx + c
descreve, geometricamente, uma parábola.
 O gráfico de uma função quadrática é composto por
três partes fundamentais:
01) Zeros da função: é ou são os pontos onde o
gráfico corta o eixo das abscissas (eixo x).
02) Vértice: ponto mais alto ou mais baixo do gráfico.
03) Termo independente: ponto que o gráfico corta
o eixo das ordenadas (eixo y). Obs: x = 0

3. Função Quadrática
• Vamos construir o gráfico da função y y
= x2 – 2x – 3 calculando os pontos citados 5
anteriormente: 4
01) Zeros da 3
função: 2
y=0 1
-2 -1 0 1 2 3 4 x
x2 – 2x – 3 = 0 -1
x=–1 x=3 -2
-3
(-1 , 0) (3, 0) -4

4. Função Quadrática
02) Vértice da função: y = x2 – y – 3
2x
5
−b −∆ 4
xv = yv =
2a 4a 3
2
− ( − 2) yv =
−16
xv = 1
2 ⋅1 4 ⋅1
-2 -1 0 1 2 3 4 x
2 − 16
xv = yv = -1
2 4
-2
xv = 1 yv = − 4
-3
V (1, − 4) -4 V

5. Função Quadrática
03) Termo Independente: y = x2 – 2x – 3
y
5
x=0 4
3
y = x2 – 2x – 3 2
1
y = (0) – 2(0) – 3
2
-2 -1 0 1 2 3 4 x
y=0–0–3 -1
-2
y=–3
-3
(0, – 3)
-4 V

6. Função Quadrática
Observaçõe y
s: 5
I: Perceba que o gráfico possui uma 4
eixo de simetria vertical, que passa
3
exatamente pelo vértice.
2
1
II: Pelo eixo de simetria percebemos
que o xv é o ponto médio entre os -2 -1 0 1 2 3 4 x
zeros da função, podendo ser -1
calculado pela média aritmética dos
-2
zeros!
−1 + 3 -3
xv = xv = 1
2 -4 V

7. Função Quadrática
y
• Vamos construir o gráfico da função 9
y = –x2 + 2x + 8: 8
01) Zeros da função:
7
y = – x2 + 2x + 8
x = – 2 (-2,0)
6
– x + 2x + 8 = 0
2
x=4 5
02) Vértice: (4,0)
−b −2 4
xv = xv = xv = 1
2a 2(−1) 3
−∆ − 36 2
yv = yv = yv = 9
4a 4(−1) 1
03) Termo independente: x=0 -2 -1 0 1 2 3 4 x
y = – x2 + 2x + 8
+8 (0, ) -1

8. Função Quadrática
Observaçõe
s: Na função y = ax2 + bx +c, a concavidade da parábola depende do
I:
valor de a:
a > a <
0 0
II: A coordenada y do vértice pode ser chamado de valor da função,
podendo ser mínimo ou máximo:
a > a < máximo
0 0
mínimo

9. Função Quadrática
III: Nem sempre o gráfico corta o eixo x em dois pontos, tendo em vista
que nem todas as funções quadráticas possuem duas raízes reais
diferentes:
∆ > 0 duas raízes ∆ = 0 duas raízes ∆ < 0 não existe
reais diferentes reais iguais raiz real
a>0
x
x x
a<0 x
x
x

10. Função Quadrática – Parte III
Ângelo Moreira dos Reis