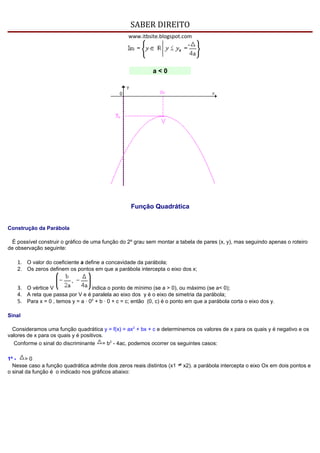
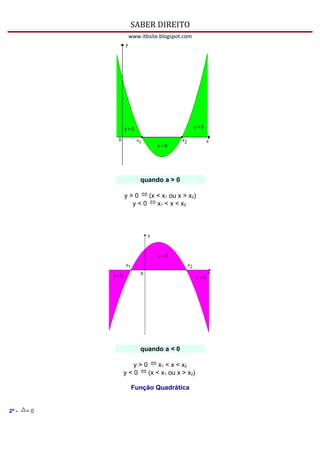
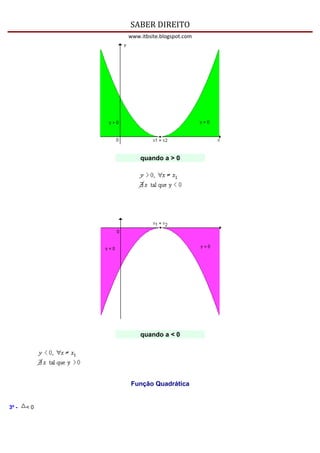
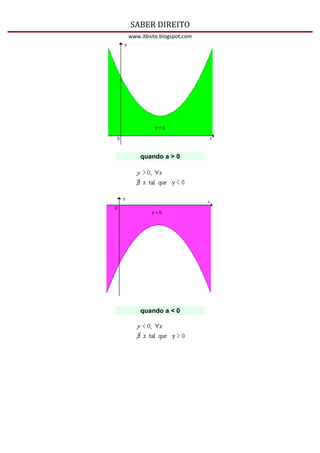
1) Uma função quadrática é uma função polinomial do 2o grau da forma f(x)=ax2+bx+c, onde a, b e c são números reais e a ≠ 0. O gráfico de uma função quadrática é uma parábola.
2) Os zeros ou raízes de uma função quadrática são as soluções da equação do 2o grau ax2+bx+c=0, dadas pela fórmula de Bhaskara. O número de raízes reais depende do sinal do discriminante.
3) As coordenadas do vértice V