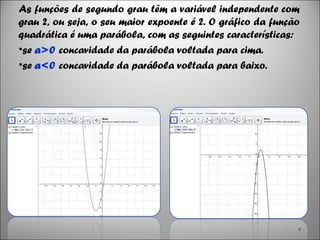
1) O documento discute a origem e definição de funções quadráticas, explicando que são expressas como f(x)=ax2+bx+c e que seu gráfico forma uma parábola. 2) Aplicações de funções quadráticas são encontradas no movimento de queda livre e trajetória de projéteis. 3) O documento também aborda como calcular os zeros da função quadrática usando a fórmula de Bhaskara.

1. Conceituando
Função Quadrática
através do
Geogebra
Grupo Ômega
Tarefa Individual Final
Informática Educativa II : Objeto de
Aprendizagem
Aluna: Luciene de Lima Ferreira
1

2. Origem da Função Quadrática
• Associa-se a idéia de equação do 2º grau, por volta de 300 a.C., em que
o matemático grego Euclides (325;265 a.C) desenvolveu uma nova
técnica denominada Álgebra Geométrica.
• Foi no Renascimento que destacou-se as tentativas de explicar o
movimento de queda livre de um corpo ou trajetória de uma bola de
canhão, que forma uma parábola. Vários teóricos dos séculos XVI e
XVII tentaram explicar essa trajetória, sem obter a parábola.
• Essas explicações foram aperfeiçoadas até se chegar à parábola
associada à curva de 2º grau, o que acelerou a necessidade de se
relacionar curvas a equações, de modo geral, álgebra à geometria.
• O adjetivo quadrática vem da palavra latina quadratum, que significa
quadrado. Um termo como x2
é chamado de quadrado em álgebra,
porque representa a área de um quadrado de lado x.
2

3. O que é uma Função Quadrática?
A função quadrática ou função do 2º grau, é expressa como
f(x)=y= ax2
+ bx + c, em que a, b e c são números reais e c
≠ 0.
Sua representação gráfica é dada em torno de eixos.
3

4. As funções de segundo grau têm a variável independente com
grau 2, ou seja, o seu maior expoente é 2. O gráfico da função
quadrática é uma parábola, com as seguintes características:
•se a>0 concavidade da parábola voltada para cima.
•se a<0 concavidade da parábola voltada para baixo.
4

5. Onde encontramos a aplicação de uma
Função Quadrática no cotidiano?
5

6. Zeros da função ou raízes
• Zero da função, ou raízes, são os valores de “x” que
anulam a função, tornando-a em f(x)=0, através dos
valores encontrados na fórmula de Bhaskara:
Discriminante (representado pela letra grega delta):
∆ = b2
– 4.a.c
6
a
acbb
xcbxaxxf
2
4
00)(
2
2 −±−
=⇒=++⇒=

7. 7

8. Bibliografia:
•Guilhermina Lobato Miranda, Maio – Agosto 2007. Limites
e possibilidades das TIC na Educação. Acesso em 30
nov. de 2010, disponível em:
<http://sisifo.fpce.ul.pt/pdfs/sisifo03PT03.pdf>
8