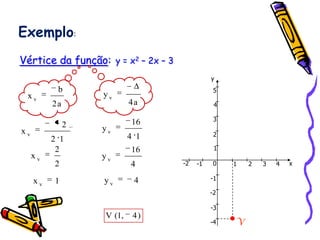
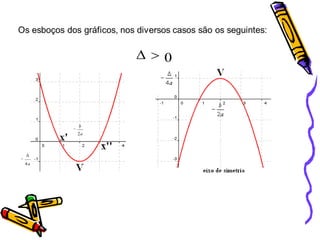
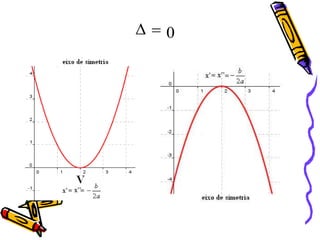
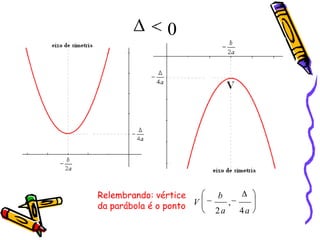
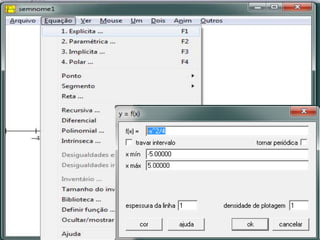
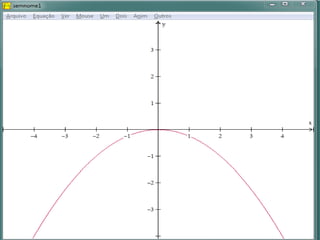
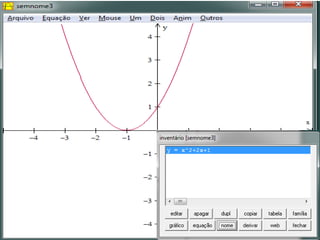
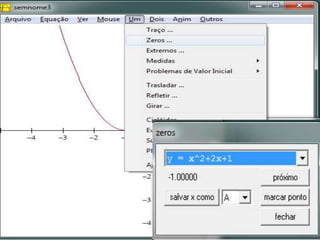
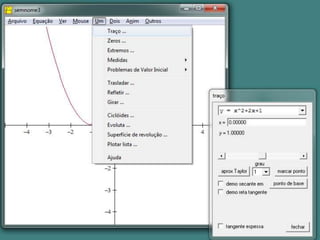
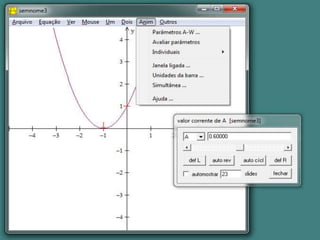
Este documento fornece instruções sobre como explorar funções quadráticas usando o software Winplot, incluindo como construir gráficos, encontrar zeros, vértices e estudar o sinal da função. Ele também discute como a variação dos parâmetros de uma função quadrática afeta sua forma gráfica.

1. Explorando as Funções
Quadráticas com o auxílio do
Winplot
Universidade Federal de Viçosa
Centro de Ciências Exatas
Departamento de Matemática
Heitor Carvalho – 68117
Lucas Silveira - 68112
Matheus Brasiel – 68101
Mayara Permanhane - 68204

2. • Links para baixar o Winplot:
• http://www.winportal.com.br/winplot
Qualquer dúvida, consultem o seguinte arquivo:
http://math.exeter.edu/rparris/peanut/Explorando%20W
http://pibid.mat.ufrgs.br/2009-
2010/arquivos_publicacoes1/indicacoes_01/aplicacoes_win
plot_PIBID_bahia1.pdfinplot%20-%20Vol%201.pdf

3. Assista ao vídeo Roda de Samba
disponível no link abaixo:
http://www.youtube.com/watch?v=apT
g7Xe3cAA

4. Função Quadrática
Definição:
A função f: R → R, dada por
f(x) = ax² + bx + c, com a, b, c
reais e a ≠ 0, denomina-se função
quadrática ou função polinomial
do 2º grau.

5. São exemplos de função de função do 2º
grau:
f(x) = x² - 4x – 3, onde a = 1, b = - 4 e c = - 3
f(x) = - 4x² + 2x, onde a = - 4, b = 2 e c = 0
f(x) = x² - 9, onde a = 1, b = 0 e c = - 9
f(x) = 6x², onde a = 6, b = 0 e c = 0

6. O gráfico de uma função quadrática é composto por três partes
fundamentais:
01) Zeros da função: é ou são os pontos em que o gráfico corta o
eixo das abscissas (eixo x), ou seja, onde y = 0.
02) Vértice: ponto mais alto ou mais baixo do gráfico.
03) Termo independente: ponto que o gráfico corta o eixo das
ordenadas (eixo y). Neste ponto x = 0.
Toda gráfico de uma função do 2° grau é uma parábola.

7. Zeros de uma Função Quadrática
Denomina-se zeros ou raízes de uma função
quadrática os valores de x que anulam a função, ou
seja, que tornam f(x) = 0.
•Se ∆ > 0, a função tem duas raízes reais e
distintos (x’ ≠ x’’).
•Se ∆ = 0, a função apresenta duas raízes reais e
iguais (x’ = x’’).
•Se ∆ < 0, a função não tem raíz real.

8. Exemplo: Vamos encontrar, se existir, os
zeros da função f(x) = x² - 4x – 5.
Solução:
054² xx
)5.(1.4)²4(
4² acb
0362016
Como ∆ > 0 a função tem dois zeros reais. Assim:
a
b
x
2
Calculemos agora seus zeros:

9. 1.2
36)4(
x
1
2
2
2
64
''
5
2
10
2
64
'
2
64
x
x
x
Logo, os zeros da função são – 1 e 5.

10. Obs: Também podemos calcular o valor do x
do vértice se fizermos a média aritmética
entre os valores de suas raízes.
Estudo do Vértice da Parábola
A parábola, que representa o gráfico da
função f(x) = ax² + bx + c, passa por um ponto V,
chamado vértice, cujas coordenadas são:
)(
2
abscissa
a
b
xv )(
4
ordenada
a
yv

11. -1 2 3
1
2
3
4
5
-2 410
-1
-2
-3
x
y
-4
Vértice da função: y = x2 – 2x – 3
a2
b
x v
a4
y v
12
2
x v
2
2
x v
1x v
14
16
y v
4
16
y v
4y v
)4,1(V
V
Exemplo:

12. Observações:
I: Na função y = ax2 + bx +c, a concavidade da parábola depende do
valor de a:
a > 0 a < 0
II: A coordenada y do vértice pode ser chamado de valor da
função, podendo ser mínimo ou máximo:
a > 0 a < 0
mínimo
máximo

13. 0
a
b
2
a4

14. 0

15. 0
Relembrando: vértice
da parábola é o ponto
aa
b
V
4
,
2

16. Construção de gráfico de uma
função quadrática usando o Winplot

19. Através do gráfico responda: qual é a concavidade da
parábola? O que acontece se alterarmos o sinal de a?
E se multiplicarmos a por uma constante maior que 1. O
que acontece? (Reflita sobre as perguntas através dos
gráficos construídos por você no Winplot)
Note que quando mudamos o sinal do coeficiente a , ela é
refletida em ralação ao eixo x, ou seja, passa a ter
concavidade voltada para cima.
Quando multiplicamos esse a por uma constante maior
que 1, a amplitude da parábola diminui isto é, se
aproxima do eixo y.

20. Agora, feche a janela. Iremos
representar o vértice da parábola de
uma função quadrática. Seja a função
dada por y = x² + 2x + 1.
Represente essa função usando os
comandos citados anteriormente e
digite na caixa de texto “x^2+2x+1”.

22. Use os comandos: “Um”  “Extremos”.
Para encontrar os zeros da função use
os comandos: “Um”  ”zeros” 
”Marcar ponto”
(OBS: Os zeros são os valores que x
assume quando y = 0, isto é, onde o
gráfico corta o eixo das abcissas).

24. • Para estudarmos o sinal da
função quadrática os comando do Winplot
que facilitam essa tarefa são: “Um”
”traço” ”marcar ponto”.

26. • Também podemos variar o valor do
coeficiente angular da função quadrática
e observar o que acontece, use os
comandos: “Anim”  “Parâmetros A – W
...”. (Escolha o parâmetro A, utilize a
barra de rolagem para fazer A variar e
verifique o que acontece para fazer o
gráfico de F).

29. Fixação:
1) Repita o procedimento anterior com as
seguintes funções:
a) Y = -x² + 6x
b) Y = x² - 4
c) Y = x² + 2x + 6
Muito obrigado!!!!!