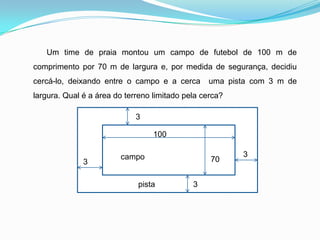
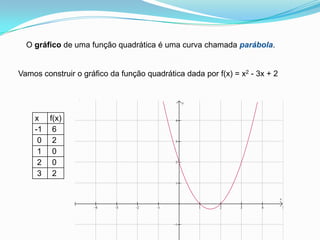
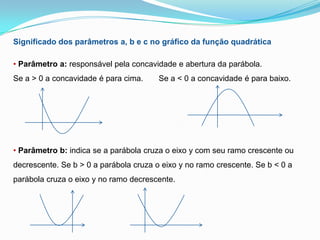
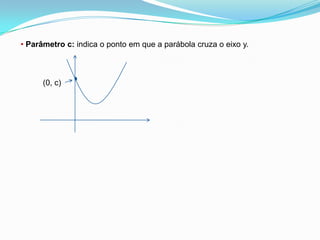
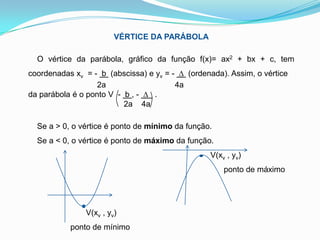
O documento discute funções quadráticas, definindo-as como funções da forma f(x) = ax2 + bx + c. Explica como calcular a área de uma região cercada usando uma função quadrática e descreve os principais elementos de uma função quadrática, incluindo vértice, raízes e forma da parábola.

1. APRENDENDO FUNÇÃO QUADRÁTICA OU FUNÇÃO POLINOMIAL DO 2º GRAUHeloisa FadelStahl

2. Um time de praia montou um campo de futebol de 100 m de comprimento por 70 m de largura e, por medida de segurança, decidiu cercá-lo, deixando entre o campo e a cerca uma pista com 3 m de largura. Qual é a área do terreno limitado pela cerca?31003campo703pista3

3. A área da região cercada é: (100 + 2 . 3) (70 + 2 . 3) = 106 . 76 = 8 056 m2Se a largura da pista fosse de 4 m, a área da região cercada seria: (100 + 2 . 4) (70 + 2 . 4) = 108 . 78 =8 424 m2Observe que a cada largura x da pista, há uma área A(x) da região cercada. E que o valor de A(x) é uma função de x dada pela expressão:A(x) = (100 + 2x) (70 + 2x) = = 7 000 + 200x + 140x + 4x2 = 4x2 + 340x + 7 000Esse é um caso particular de função quadrática ou função polinomial do 2 º grau.

4. Chama-se função quadrática ou função polinomial do 2 º grau, qualquer função f de R em R dada por uma lei da forma f(x) = ax2 +bx + c, em que a, b e c são números reais e a ≠ 0.Veja alguns exemplos de funções quadráticas: f(x) = 2 x2 + 3x + 5, sendo a = 2, b = 3 e c = 5 f(x) = 3 x2 - 4x + 1, sendo a = 3, b = - 4 e c = 1 f(x) = x2 - 1, sendo a = 1, b = 0 e c = - 1 f(x) = - x2 + 2x, sendo a = - 1, b = 2 e c = 0 f(x) = - 4 x2 , sendo a = - 4, b = 0 e c = 0

5. O gráfico de uma função quadrática é uma curva chamada parábola.Vamos construir o gráfico da função quadrática dada por f(x) = x2 - 3x + 2

6. Significado dos parâmetros a, b e c no gráfico da função quadráticaParâmetro a: responsável pela concavidade e abertura da parábola.Se a > 0 a concavidade é para cima. Se a < 0 a concavidade é para baixo.Parâmetro b: indica se a parábola cruza o eixo y com seu ramo crescente ou decrescente. Se b > 0 a parábola cruza o eixo y no ramo crescente. Se b Parâmetro c: indica o ponto em que a parábola cruza o eixo y. (0, c)

7. ZEROS OU RAÍZES DA FUNÇÃO QUADRÁTICAZeros ou raízes da função quadrática f(x)= ax2 + bx + c são os valores de x para os quais a função se anula, ou seja, f(x) = 0. Assim, os zeros da função quadrática f(x)= ax2 +bx +c são as soluções da equação do 2º grau ax2 +bx + c = 0, as quais são dadas pela fórmula:x = - b ± √ b2 – 4ac2aVamosobteros zeros dafunção f(x) = x2 - 3x + 2.Temos a = 1, b = - 3 e c = 2Então, aplicando a fórmula, as raízessão: x’ = 1 e x’’ = 2.

8. VÉRTICE DA PARÁBOLAO vértice da parábola, gráfico da função f(x)= ax2 + bx + c, tem coordenadas xv = - b (abscissa) e yv = - ∆ (ordenada). Assim, o vértice 2a 4a da parábola é o ponto V - b , - ∆ . 2a 4a Se a > 0, o vértice é ponto de mínimo da função.Se a < 0, o vértice é ponto de máximo da função. V(xv , yv) ponto de máximo V(xv , yv) ponto de mínimo

9. AS ORIGENS DA PARÁBOLANão há unanimidade sobre como a curva plana conhecida como parábola foi introduzida na matemática. Segundo a versão mais difundida, ela teria surgido dos esforços de Menaecmo (c. IV a.C.), um discípulo de Aristóteles (384-322 a.C.), para resolver o chamado “problema deliano”, cuja origem é muito curiosa. Assolados por uma devastadora peste, os habitantes da ilha de Delos (os delianos) recorreram aos préstimos de seu oráculo, que sugeriu , para afastar o mal, que eles construíssem um altar cúbico cujo volume fosse o dobro do já existente consagrado ao deus Apolo. E a parábola tem sua origem na busca dessa solução.

10. APLICAÇÕES DA PARÁBOLA

17. BIBLIOGRAFIA:DANTE, L. R. (2005) Matemática. São Paulo: Editora Ática.IEZZI, G.et al. (2004) Matemática: Ciência e Aplicações. 2ª Ed. São Paulo: Atual