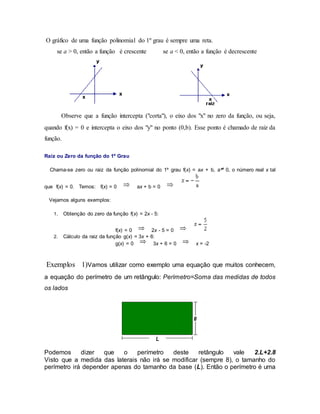
Este documento descreve as funções polinomiais do 1o grau, também chamadas de funções afins. Estas funções possuem a forma geral f(x) = ax + b, onde a é o coeficiente angular e b é o coeficiente linear. O gráfico de uma função do 1o grau é sempre uma reta, e sua raiz ou zero é encontrada quando f(x) = 0. Exemplos e exercícios são fornecidos para ilustrar o conceito.

1. Função Polinomial do 1º Grau
http://www.cursinho.hpg.ig.com.br/index.html?http://www.cursinho.hpg.ig.com.br/materias/funcoes/f
uncao1g.html
http://www.exatas.hpg.ig.com.br/funcao1.htm
http://www.somatematica.com.br/emedio/funcao1/ funcao1.php
Uma função cuja lei de formação seja dada pela sentença f(x) = c, com c sendo um
número real qualquer, é dita função constante, pois não depende de x.
Ex.: a) f(x) = 2 b) g(x) = –4 c) h(x) = 1/3 d) y=-3
O gráfico de uma função constante é sempre uma reta paralela ao eixo das abscissas
ou eixo dos "x".
y
3 y=3
x
Uma função real, f: IR  IR, cuja lei de formação é dada pela sentença f(x) = a.x + b,
onde a é denominado de taxa de variação ou coeficiente angular e b de coeficiente linear é
dita função polinomial do 1º grau ou função afim. Quando b = 0, a função polinomial do
1º grau f(x) = a.x é denominada de função linear. A função linear cujo valor de a é 1, e daí
f(x) = x é denominada função idêntica, unidade ou identidade.
Ex.: a) f(x) = 3x + 2 b) y = –3x – 1 c) f(x) = 2/3 x d) f(x) = x
Exemplos.
a) f(x)=2x+6 a=2 b=6 b) f(x)=8x a=8 b=0 c) y= -3x+5 a=-3 b=5
d)y=-3x+2 a=-3/4 b=2/4=1/2 e) f(x) =4 a=0 b=4
4
Em todos os exemplos, x é a variável independente, e y a variável dependente

2. O gráfico de uma função polinomial do 1º grau é sempre uma reta.
se a > 0, então a função é crescente se a < 0, então a função é decrescente
Observe que a função intercepta ("corta"), o eixo dos "x" no zero da função, ou seja,
quando f(x) = 0 e intercepta o eixo dos "y" no ponto (0,b). Esse ponto é chamado de raiz da
função.
Raiz ou Zero da função do 1º Grau
Chama-se zero ou raiz da função polinomial do 1º grau f(x) = ax + b, a 0, o número real x tal
que f(x) = 0. Temos: f(x) = 0 ax + b = 0
Vejamos alguns exemplos:
1. Obtenção do zero da função f(x) = 2x - 5:
f(x) = 0 2x - 5 = 0
2. Cálculo da raiz da função g(x) = 3x + 6:
g(x) = 0 3x + 6 = 0 x = -2
Exemplos 1)Vamos utilizar como exemplo uma equação que muitos conhecem,
a equação do perímetro de um retângulo: Perímetro=Soma das medidas de todos
os lados
Podemos dizer que o perímetro deste retângulo vale 2.L+2.8
Visto que a medida das laterais não irá se modificar (sempre 8), o tamanho do
perímetro irá depender apenas do tamanho da base (L). Então o perímetro é uma

3. função do Lado L. E por isso L é a variável independente, e o perímetro
dependente.
Perímetro=2.L+2.8 f(x)=2.x+16 ou y = 2.x+16
2-Numa loja, o salário fixo mensal de um vendedor é 500 reais. Além disso, ele recebe
de comissão 50 reais por produto vendido.
a) Escreva uma equação que expresse o ganho mensal y desse vendedor, em função
do número x de produto vendido.
y=salário fixo + comissão y=500 + 50x
b) Quanto ele ganhará no final do mês se vendeu 4 produtos?
y=500+50x , onde x=4 y=500+50.4 = 500+200 = 700
c) Quantos produtos ele vendeu se no final do mês recebeu 1000 reais?
y=500+50x , onde y=1000 1000=500+50x » 50x=1000-500 » 50x=500 » x=10
Gráficos da função polinomial do primeiro grau
O gráfico de uma função polinomial do 1º grau é sempre uma reta.
Exemplos:
Este exemplo tem o coeficiente angular a=2, raiz –2/3 então a função é crescente.

4. Este exemplo tem o coeficiente angular a=-1/2, e
raiz 4, então a reta é decrescente.
Este exemplo tem o coeficiente angular a=0, então a
função é constante.
* Coeficiente Linear
O coeficiente linear é o número que fica no final da função, quando a função está
no formato geral (y=ax+b). E este coeficiente é muito útil quando queremos
desenhar o gráfico de uma função do primeiro grau, ele nos diz nada mais nada
menos do que o ponto em que a reta corta o eixo Y (eixo vertical).
Exemplos: Função do 1º grau – Aplicação prática
1) O preço a pagar por uma corrida de táxi depende da distância percorrida. A
tarifa P é composta por duas partes: uma parte fixa, denominada bandeirada e
uma parte variável que depende do número d de quilômetros rodados.
Suponha que a bandeirada esteja custando R$ 2,00 e o quilômetro rodado, R$
1,50.
a) Expresse o preço P em função da distância d percorrida.
b) Quanto se pagará por uma corrida em que o táxi rodou 10 km?
c) Sabendo que a corrida custou R$ 20,00, calcule a distância percorrida
pelo táxi.
d) represente o gráfico da função

5. 2) Uma piscina de 3000 litros, totalmente cheia, precisa ser esvaziada para
limpeza e para isso uma bomba que retira água à razão de 100 litros por
minuto foi acionada. Baseado nessas informações, pede-se:
a) a expressão que fornece o volume (V) de água na piscina em função do
tempo (t) que a bomba fica ligada.
b) a expressão que fornece o volume de água que sai da piscina (VS) em
função do tempo (t) que a bomba fica ligada.
c) o tempo necessário para que a piscina seja esvaziada.
d) quanto de água ainda terá na piscina após 3 horas de funcionamento da
bomba?
e) o esboço do gráfico que representa o volume de água na piscina em
função do tempo em que a bomba fica ligada.
Exercícios de fixação:
1) Dadas as funções
1
f(x)  x  e g(x)  2x  4 , calcule f(2) + g(-3)
2
2) faça os gráficos das seguintes funções , determinando sua raiz:
a) y = 2x + 3 b)
3x 1
2
y
 
 c) y = –x
3) Em uma determinada loja, o salário mensal fixo de um vendedor é de R$
240,00. Além disso, ele recebe R$ 12,00 por unidade vendida.
a) Expresse o ganho mensal (S) desse vendedor em função do número (u) de
unidades vendidas.
b) Quantas unidades ele deve vender para receber um salário de R$ 700,00 ?
4) Um botijão de cozinha contém 13 kg de gás. Sabendo que em média é
consumido, por dia, 0,5 kg de gás:
a) Expresse a massa (m) de gás no botijão, em função do número (t) de dias
de consumo.
b) esboce o gráfico desta função.
c) Depois de quantos dias o botijão estará vazio ?
5) A água congela a 0° C e a 32° F; ferve a 100° C e 212° F. A temperatura em
graus Fahrenheit (F) varia linearmente com a temperatura em graus Celsius
(C).
a) Expresse a temperatura em F em função de C e faça o gráfico desta
função.

6. b) A temperatura do corpo humano não febril é de 37° C. Qual é esta
temperatura em graus Fahrenheit?
c) que temperatura, em graus Celsius, corresponde 20° F.
d) represente o gráfico da função
6)Um táxi cobra R$2,60 de bandeirada e mais R$0,40 por quilômetro
quadrado. Ao final de um percurso de p quilômetros, o taxímetro marca
R$8,20. O valor de p é:
a) 10 b) 11 c) 12 d) 13 e) 14
7)Dois táxis têm preços dados por:
Táxi A: bandeirada a R$ 4,00, mais R$ 0,75 por quilômetro rodado;
Táxi B: bandeirada a R$ 3,00, mais R$ 0,90 por quilômetro rodado.
a) Obtenha a expressão que fornece o preço de cada táxi (PA e PB) em
função da distância percorrida.
b) Para que distâncias é vantajoso tomar cada táxi ?
8)O preço de uma máquina nova é R$2.000,00. Sabendo-se que
o valor da máquina diminui com o tempo em R$ 50,00 por mês
e a relação entre o preço y e o tempo t é dada pela
equação y = at + b, e que daqui a 12 meses o preço será de
?
Gráfico da função do 1º grau:
O gráfico de uma função do 1º grau de R em R é uma reta.
Exemplo:
1) Construa o gráfico da função determinada por f(x)=x+1:
Utilizando o excel , simulador do aprendebrasil e graphmatica
Atribuindo valores reais quaisquer para x, obtemos seus valores correspondentes
para y.
D(f) = {-2,-1,0,1,2}

7. x y=f(x)=x+1
-2 -1
-1 0(raiz)
0 1
1 2
2 3
O conjunto dos pares ordenados determinados
é f={(-2,-1),(-1,0),(0,1),(1,2),(2,3)}
2) Construa o gráfico da função determinada por f(x)=-x+1.
Atribuindo valores reais para x, obtemos seus valores correspondentes para y.
x y=f(x)=-x+1
-2 3
-1 2
0 1
1 0(raiz)
2 -1
O conjunto dos pares ordenados determinados é
f={(-2,3),(-1,2),(0,1),(1,0),(2,-1)}
Gráficos y = x+1 ( a> 0 ) ; onde a = 1 é crescente e o gráfico y = -x+1 ( a<0 ); onde
a=-1 é decrescente
Raiz ou zero da função do 1º grau:
Para determinarmos a raiz ou zero de uma função do 1º grau,
definida pela equação y=ax+b, como a é diferente de 0, basta
obtermos o ponto de intersecção da equação com o eixo x,
que terá como coordenada o par ordenado (x,0).

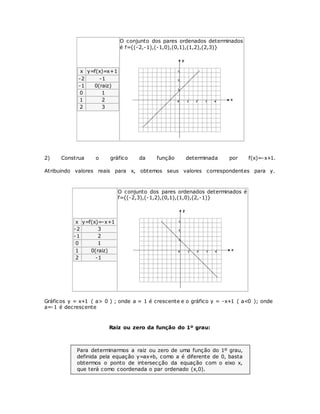
8. 1) Considere a função dada pela equação y=x+1, determine a raiz desta função.
[Sol] Basta determinar o valor de x para termos y=0
x+1=0 » x=-1
Dizemos que -1 é a raiz ou zero da função.
Note que o gráfico da função y=x+1, interceptará (cortará) o eixo x em -1, que é a
raiz da função.
2) Determine a raiz da função y=-x+1 e esboce o gráfico.
Fazendo y=0, temos: 0 = -x+1 » x = 1
Gráfico:
Note que o gráfico da função y=-x+1, interceptará (cortará) o eixo x em 1, que é a
raiz da função.

9. Ponto de encontro ou ponto de intersecção entre funções
É o ponto onde o valor de x e y são os mesmos para as duas funções. Esse ponto
é obtido quando igualamos o valor de y da função1 com o valor de y da função 2.
Observe o exemplo 1
Uma caixa com 80 litros de água, esvazia 2 litros de água por minuto, em quanto
uma outra caixa com 30 litros, enche de água a razão de 3 litros por minuto.Se as
duas caixas trabalham ao mesmo tempo,após quanto tempo as caixas terão os
mesmos volumes. Qual é esse volume?
Graficamente temos: utilizar suporte gráfico para visualizar o problema
tempo(mim) v1=80-2.t v2=30+3t
0 80 30
2 76 36
4 72 42
6 68 48
8 64 54
10 60 60
12 56 66
100
80
60
40
20
0
0 2 4 6 8 10 12
v1=80-2.t
v2=30+3t
Algebricamente temos v1 = v2 então:
80-2t = 30+3t => 80-30=3t+2t => 50 = 5t => t = 50/5 => t =10 mim
calculando o volume v1 = 80-2(10) => v1 = 80-20 => v1 = 60 m3