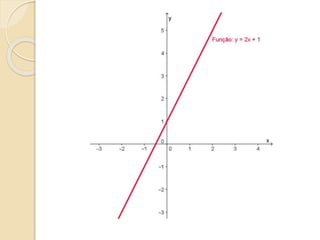
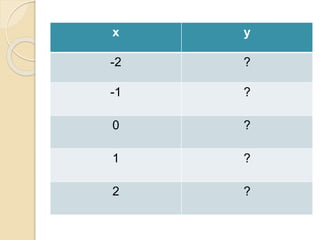
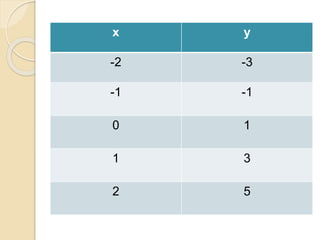
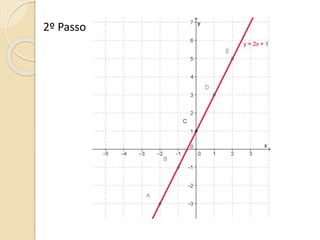
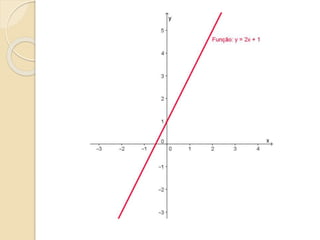
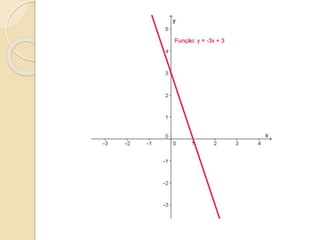
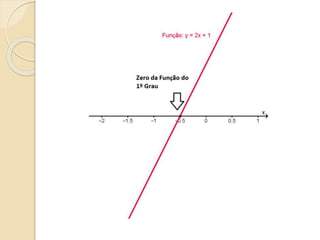
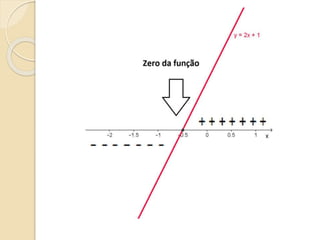
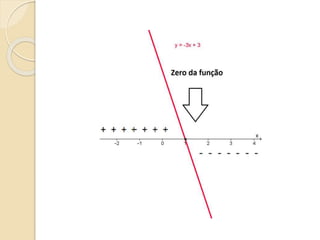
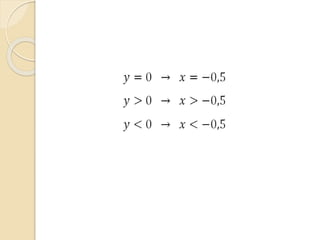Este documento discute as funções do primeiro grau, incluindo como escrever equações de funções lineares, determinar seus coeficientes angular e linear, plotar gráficos, calcular raízes e estudar os sinais. Recomenda assistir a um vídeo e usar o programa Geogebra para explorar conceitos interativos de geometria e álgebra relacionados a estas funções.

1. Função do 1º Grau

2. Função do 1º Grau
Para iniciarmos nosso estudo sobre
esta função, vamos assistir a um
vídeo, que nos mostrará a importância
desta para nosso dia-a-dia.

3. Para aprendermos um pouco mais,
vamos recorrer a um programa
chamado Geogebra.
O GeoGebra é um aplicativo
de matemática dinâmica que combina
conceitos de geometria e álgebra. Sua
distribuição é livre, nos termos
da GNU, e foi criado por Markus
Hohenwarter para ser utilizado em
ambiente de sala de aula.

4. Convido você para assistir esse vídeo e
a usar esse programa como aliado
nessa jornada na Matemática. Você
poderá pesquisar na Web como usá-
lo.

5. É importante lembrar que em uma
função tem-se para cada valor de “x”
um valor para “y”. Observe:
Exemplo:
y=2x+1
-Se admitir que o x=1, o valor de y=3
y=2.1+1 y=3
-Se admitir que o x=0, o valor de y=1
y=2.0+1 y=1
Funçã
o

6. Função do 1º Grau
Toda função do 1º grau pode ser escrita
da seguinte forma:
Sabendo-se que:
Ex:
1) y=2x+1
2) y=-3x+3

7. Coeficiente “angular” e
“linear”
O “a” é o coeficiente angular da função
do 1º grau.
O “b” é o coeficiente linear da função do
1º grau.
Exemplos:
1) y=2x+1 2) y=-3x+3
a=2 a=-3
b=1 b=3

8. Gráfico da Função do 1º Grau
A função do 1º Grau, descreve uma
reta.
Exemplo:
y=2x+1

10. Para obtê-la deve-se:
-atribuir valores reais para “x” e obter os
valores de “y”, organizando os valores
em uma tabela
-localizar no plano cartesiano os pontos
(x,y) e traçar a reta que passa por
eles.

11. x y
-2 ?
-1 ?
0 ?
1 ?
2 ?

13. x y
-2 -3
-1 -1
0 1
1 3
2 5

14. 2º Passo

15. Função Crescente ou
Decrescente
De acordo com o sinal de “a”, a função
do 1º Grau pode ser: Crescente ou
Decrescente:
Se “a” for positivo a função é Crescente
Exemplo:
y=2x+1
a=2 (o valor de “a” é positivo)
Observe:

17. Se “a” for negativo a função é
Decrescente
Exemplo:
y=-3x+3
a=-3 (o valor de “a” é negativo)
Observe:

19. Raiz ou zero de uma função do
1º Grau
Para determinar o zero de uma função
do 1º Grau é necessário que você
iguale a função a zero. Veja:
Exemplo:
y=2x+1 y=0
Então:
2x+1=0 2x=-1 x=-1/2
x=-0,5

20. Determinar o zero de uma função do 1º
Grau, significa determinar em que
ponto a função corta o eixo dos “x” no
plano cartesiano.
Como no exemplo que segue:

22. Estudo dos sinais da função do
1º Grau
Consiste em saber para que valores de
“x”:
y>0 (positivo)
y=0 (nulo)
y<0 (negativo)

23. 1º Caso: Função Crescente
Exemplo:
y=2x+1
Determina-se o zero da função do 1º
Grau:
x=-0,5
A partir daí vamos estudar os sinais da
função :

26. 2º Caso: Função decrescente
Exemplo: y=-3x+3
Determina-se o zero da função do 1º
Grau:
x=1
A partir daí vamos estudar os sinais da
função :

29. Referências:
http://www.youtube.com/watch?v=Lnwz
3gIzni0
Matemática aula por aula: volume
único: ensino médio / Benigno Barreto
Filho, Claúdio Xavier da Silva – São
Paulo: FTD, 2000.
http://www.youtube.com/watch?v=swYH
NtmODG8