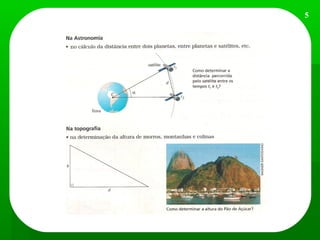
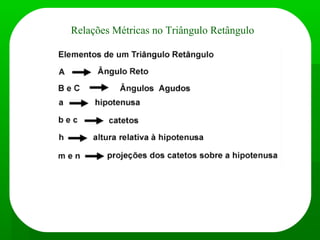
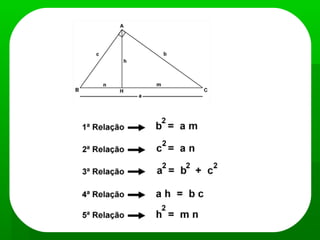
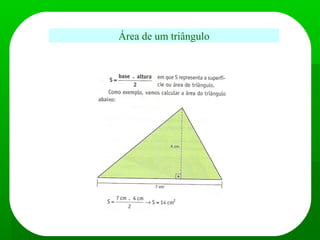
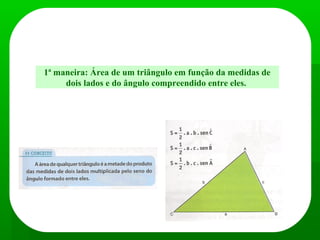
Trigonometria estuda as medidas dos triângulos. Inclui o Teorema de Pitágoras que relaciona os lados de um triângulo retângulo, e as funções seno, cosseno e tangente que relacionam os lados e ângulos de um triângulo retângulo. Também inclui o Teorema dos Senos e dos Cossenos que podem ser usados para resolver problemas envolvendo qualquer triângulo quando são conhecidas algumas medidas.

2. Trigonometria
O significado da palavra trigonometria, vem do grego e resulta da
conjunção de três palavras:
Tri – três
Gonos – ângulo
Metrein - medir
Trigonometria significa, o estudo das medidas dos triângulos.

4. Algumas aplicações da Trigonometria

5. 5

6. 6

7. Triângulo retângulo
Triângulo retângulo é todo triângulo que apresenta um ângulo reto, ou
seja, um ângulo de 90°.
catetocateto
hipotenusa
cateto
cateto
hipotenusa
A hipotenusa é sempre o maior lado do triângulo retângulo;
Em qualquer triângulo, a soma dos ângulos internos é sempre 180°;
Como num triângulo retângulo um dos ângulos é reto, a soma dos outros
dois ângulos agudos (menores que 90º) é sempre 90°;
Quando a soma de dois ângulos internos é igual a 90°, dizemos que esses
ângulos são complementares.

8. Teorema de Pitágoras
Em todo triângulo retângulo, o quadrado da medida da hipotenusa é
igual a soma dos quadrados das medidas dos catetos.
c = 4
b = 3
a = 5
2525
16925
435 222
222
=
+=
+=
+= cba

9. Relações Métricas no Triângulo Retângulo

11. Teorema de Tales
Um feixe de retas paralelas, intersectado por duas transversais,
determina, sobre essas transversais segmentos proporcionais.
Exemplo de aplicação:

12. Relações Trigonométricas num triângulo retângulo
Seno

13. Cosseno

14. Tangente

15. Exemplo de aplicação:

16. Relações entre seno, cosseno e tangente

17. 22

18. Teorema ou Lei dos Senos
A lei dos senos pode ser utilizada em
qualquer triângulo. No caso de
triângulos retângulos, basta considerar
sen 90° = 1.

19. Teorema ou Lei dos Cossenos
A Lei dos Cossenos é geralmente usada, quando são conhecidas as medidas de
dois lados e o ângulo formado por eles.

20. Exemplo:

21. Área de um triângulo

22. Existem problemas em que se deseja calcular a área de um triângulo
e não são conhecidas as medidas da base e altura. Nesses casos,
a área pode ser calculada de duas maneiras diferentes:
1ª maneira: Área de um triângulo em função da medidas de
dois lados e do ângulo compreendido entre eles.

23. 2ª maneira: Fórmula de Heron