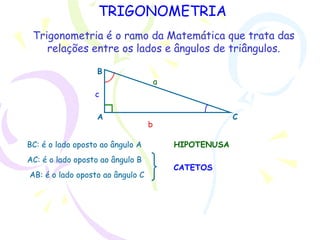
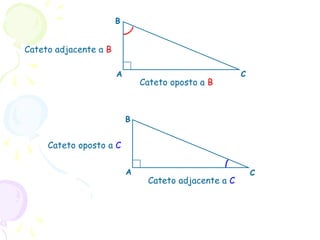
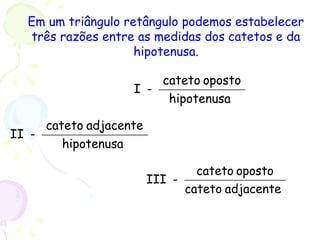
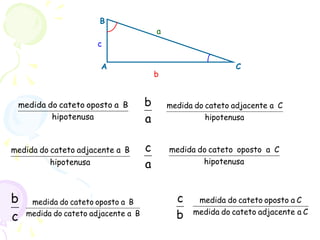
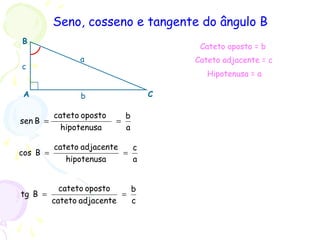
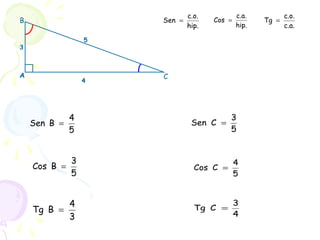
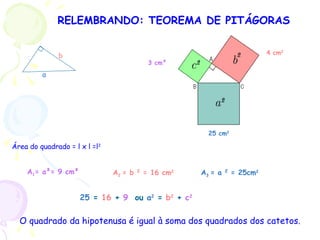
O documento apresenta um resumo sobre trigonometria, descrevendo sua origem na antiguidade com civilizações babilônica e egípcia e seu desenvolvimento pelos gregos e indianos. Explica conceitos básicos como funções trigonométricas, razões trigonométricas e o Teorema de Pitágoras, e apresenta exemplos de aplicações da trigonometria.

1. Revisão:
TRIGONOMETRIA

2. A trigonometria começou com as
civilizações babilônica e egípcia e
desenvolveu-se na Antiguidade graças
aos gregos e indianos.
A partir do século VIII d.C.,
astrônomos islâmicos aperfeiçoaram as
descobertas gregas e indianas,
notadamente em relação às funções
trigonométricas.

3. Algumas aplicações da trigonometria são:
 Determinação da altura de um certo prédio.
 Os gregos determinaram a medida do raio de terra, por
um processo muito simples.
 Seria impossível se medir a distância da Terra à Lua,
porém com a trigonometria se torna simples.
 Um engenheiro precisa saber a largura de um rio para
construir uma ponte, o trabalho dele é mais fácil quando
ele usa dos recursos trigonométricos.
 Um cartógrafo (desenhista de mapas) precisa saber a
altura de uma montanha, o comprimento de um rio, etc.
Sem a trigonometria ele demoraria anos para desenhar
um mapa.

4. TRIGONOMETRIA
A
B
C
a
b
c
BC: é o lado oposto ao ângulo A
AC: é o lado oposto ao ângulo B
AB: é o lado oposto ao ângulo C
HIPOTENUSA
CATETOS
Trigonometria é o ramo da Matemática que trata das
relações entre os lados e ângulos de triângulos.

5. A
B
C
A
B
C
Cateto adjacente a B
Cateto oposto a C
Cateto oposto a B
Cateto adjacente a C

6. Em um triângulo retângulo podemos estabelecer
três razões entre as medidas dos catetos e da
hipotenusa.
adjacentecateto
opostocateto
-III
hipotenusa
opostocateto
-I
hipotenusa
adjacentecateto
-II

7. A
B
C
a
b
c
a
b
a
c
c
b
hipotenusa
Baopostocatetodomedida
hipotenusa
Baadjacentecatetodomedida
Baadjacentecatetodomedida
Baopostocatetodomedida
hipotenusa
Caadjacentecatetodomedida
hipotenusa
Caopostocatetodomedida
Caadjacentecatetodomedida
Caopostocatetodomedida
b
c

8. hipotenusa
opostocateto
-I
hipotenusa
adjacentecateto
-II
adjacentecateto
opostocateto
-III
Essas razões são chamadas RAZÕES TRIGONOMÉTRICAS
e recebem o nome de:
SENO
COSSENO
TANGENTE

9. Seno, cosseno e tangente do ângulo B
A
B
C
c
b
a
a
b
hipotenusa
opostocateto
Bsen ==
a
c
hipotenusa
adjacentecateto
Bcos ==
c
b
adjacentecateto
opostocateto
Btg ==
Cateto oposto = b
Cateto adjacente = c
Hipotenusa = a

10. Seno, cosseno e tangente do ângulo C
A
B
C
c
a
b
b
c
adjacentecateto
opostocateto
Ctg ==
a
c
hipotenusa
opostocateto
Csen ==
a
b
hipotenusa
adjacentecateto
Ccos ==
Cateto oposto = c
Cateto adjacente = b
Hipotenusa = a

11. 5
3
4
A
B
C
5
4
BSen =
5
3
BCos =
3
4
BTg =
5
3
CSen =
5
4
CCos =
4
3
CTg =
c.a.
c.o.
Tg =
hip.
c.o.
Sen =
hip.
c.a.
Cos =

12. RELEMBRANDO: TEOREMA DE PITÁGORAS
3 cm²
4 cm2
25 cm2
Área do quadrado = l x l =l2
A1= a²= 9 cm² A2 = b 2
= 16 cm2
A3 = a 2
= 25cm2
a
bc
25 = 16 + 9 ou a2
= b2
+ c2
O quadrado da hipotenusa é igual à soma dos quadrados dos catetos.

13. θ
1) No triângulo abaixo, determine o sen θ, cos θ e tg θ:
4
3
=
.a.c
.o.c
=θtg
5
4
=
hip
.a.c
=θcos
5
3
=
hip
c.o.
=θsen
Exercícios resolvidos

14. 2) Calcule o perímetro do triângulo retângulo ABC da figura, sabendo
que o segmento BC é igual a 10 m e cos α = 3/5 .
6mx305x
10
x
5
3
hip
c.a.
αcos
=→=→=
=
α (
C
BA
10m
x
y
Utilizando o teorema de Pitágoras, encontramos o valor de y:
10² = 6² + y² 100 = 36 + y² y² = 100 – 36→ → → y² = 64 → y = 8m
Calculando o perímetro:
2p = x + y + 10
2p = 6 + 8 + 10 = 24 m