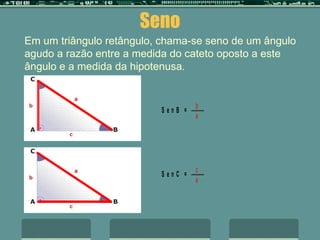
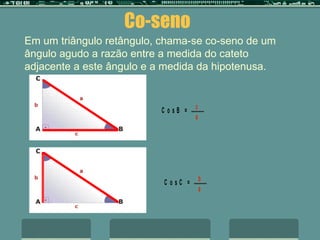
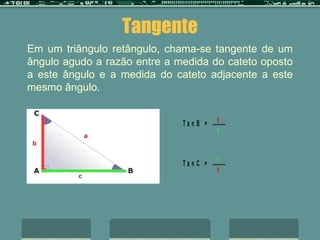
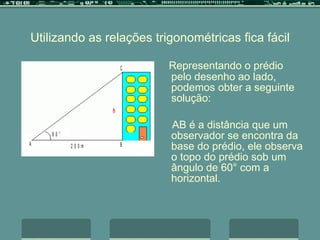
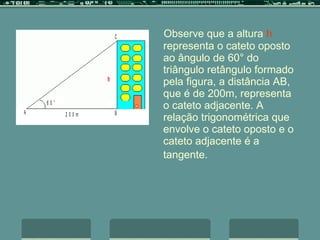
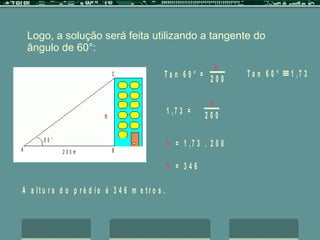
O documento discute a trigonometria em triângulos retângulos, definindo seno, co-seno e tangente em termos das relações entre os lados e ângulos. Ele fornece um exemplo de como calcular a altura de um prédio usando a tangente do ângulo de 60 graus e as relações trigonométricas.

1. A Trigonometria A Trigonometria no Triângulo Retângulo José Eduardo de Sousa

2. A Trigonometria no Triângulo Retângulo A trigonometria é o ramo da Matemática que se atém ao estudo do triângulo, analisando as relações entre os seus ângulos e lados. A abordagem trigonométrica é bastante ampla, podendo ser aplicada à Astronomia, à Cartografia, às Ciências Naturais, dentre outras.

3. Razões Trigonométricas de um Triângulo Retângulo Considere o triângulo retângulo ABC, na figura ao lado, cujos catetos são definidos por b e c e cuja hipotenusa é dada por a .

4. Seno Em um triângulo retângulo, chama-se seno de um ângulo agudo a razão entre a medida do cateto oposto a este ângulo e a medida da hipotenusa .

5. Co-seno Em um triângulo retângulo, chama-se co-seno de um ângulo agudo a razão entre a medida do cateto adjacente a este ângulo e a medida da hipotenusa. .

6. Tangente Em um triângulo retângulo, chama-se tangente de um ângulo agudo a razão entre a medida do cateto oposto a este ângulo e a medida do cateto adjacente a este mesmo ângulo.

7. Valores do Seno do ângulo de 60º Podemos obter os valores do seno, do co-seno e da tangente dos ângulos de 0º a 89º, construindo os triângulos retângulos com os respectivos ângulos. Veja a seguir o exemplo com o ângulo de 60º.

8. Seno, co-seno e tangente dos ângulos notáveis Ângulos notáveis são os ângulos cujos valores do seno, co-seno e tangente são mais utilizados. São eles: 30°, 45° e 60°.

9. Aplicação Como calcular a altura de um prédio como esse?

10. Utilizando as relações trigonométricas fica fácil Representando o prédio pelo desenho ao lado, podemos obter a seguinte solução: AB é a distância que um observador se encontra da base do prédio, ele observa o topo do prédio sob um ângulo de 60° com a horizontal.

11. Observe que a altura h representa o cateto oposto ao ângulo de 60° do triângulo retângulo formado pela figura, a distância AB, que é de 200m, representa o cateto adjacente. A relação trigonométrica que envolve o cateto oposto e o cateto adjacente é a tangente.

12. Logo, a solução será feita utilizando a tangente do ângulo de 60°:

13. Referências: www.profezequias.net/trigonometria.html www.tosabendomais.com.br www.brasilescola.com/matematica