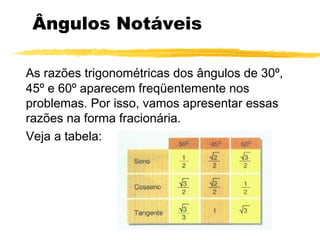
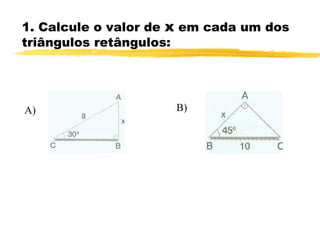
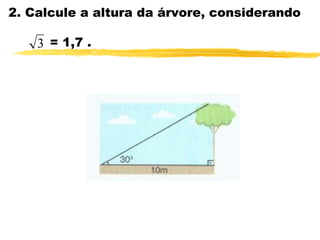
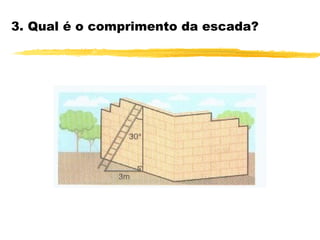
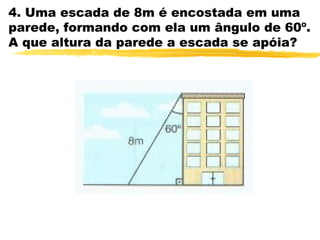
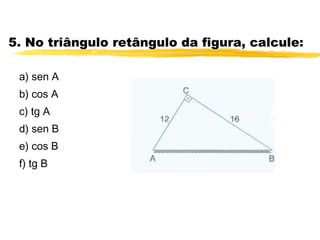
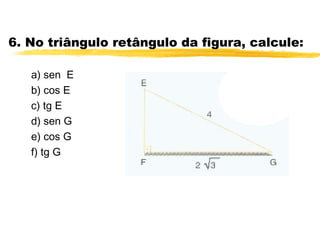
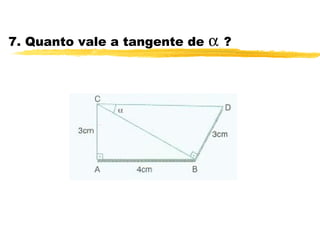
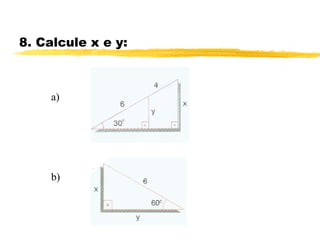
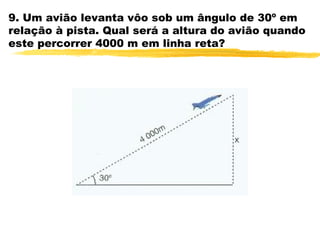
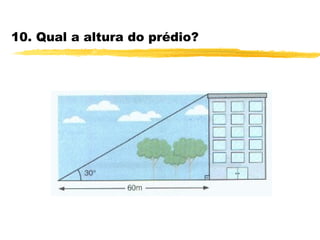
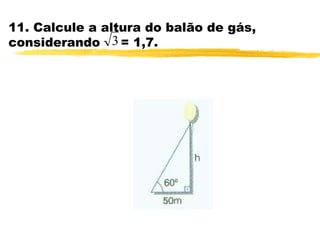
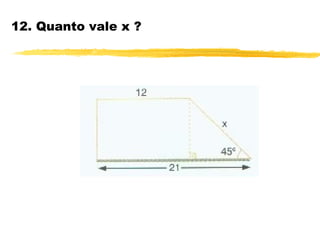
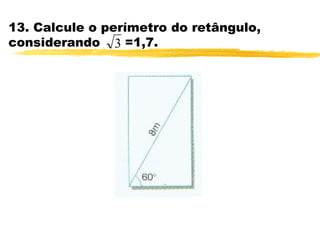
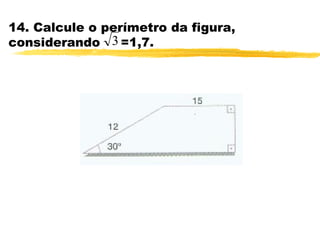
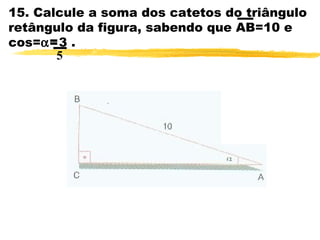
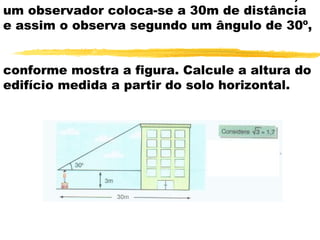
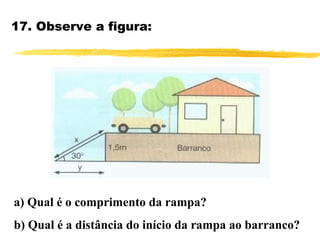
O documento discute trigonometria em triângulos retângulos. Explica que a trigonometria mede as relações entre os lados e ângulos de um triângulo retângulo, definindo seno, cosseno e tangente em termos de catetos e hipotenusa. Fornece exemplos numéricos de razões trigonométricas para ângulos de 30°, 45° e 60°. Contém exercícios sobre cálculos trigonométricos em triângulos retângulos.

1. TRIGONOMETRIA NO
TRIÂNGULO RETÂNGULO

2. O que é trigonometria?
Assim, trigonometria significa medição de três
ângulos. Este ramos da Matemática estuda a
relação entre as medidas dos lados e dos ângulos
de um triângulo. A trigonometria é empregada na
navegação, na aviação, na topografia etc., sendo
indispensável à Engenharia e à Física.

3. Seno, cosseno e tangente no
triângulo retângulo
Para um ângulo agudo de um triângulo
retângulo definimos seno, cosseno e
tangente como segue:

4. O seno do ângulo é a razão entre o
cateto oposto ao ângulo e a hipotenusa.

5. O cosseno do ângulo é a razão entre o
cateto adjacente ao ângulo e a hipotenusa.

6. A tangente do ângulo é a razão entre o
cateto oposto e o cateto adjacente ao ângulo.

7. Ângulos Notáveis
As razões trigonométricas dos ângulos de 30º,
45º e 60º aparecem freqüentemente nos
problemas. Por isso, vamos apresentar essas
razões na forma fracionária.
Veja a tabela:

8. Exercícios

9. 1. Calcule o valor de x em cada um dos
triângulos retângulos:
A) B)

10. 2. Calcule a altura da árvore, considerando
= 1,7 .3

11. 3. Qual é o comprimento da escada?

12. 4. Uma escada de 8m é encostada em uma
parede, formando com ela um ângulo de 60º.
A que altura da parede a escada se apóia?

13. 5. No triângulo retângulo da figura, calcule:
a) sen A
b) cos A
c) tg A
d) sen B
e) cos B
f) tg B

14. 6. No triângulo retângulo da figura, calcule:
a) sen E
b) cos E
c) tg E
d) sen G
e) cos G
f) tg G

15. 7. Quanto vale a tangente de α ?

16. 8. Calcule x e y:
a)
b)

17. 9. Um avião levanta vôo sob um ângulo de 30º em
relação à pista. Qual será a altura do avião quando
este percorrer 4000 m em linha reta?

18. 10. Qual a altura do prédio?

19. 11. Calcule a altura do balão de gás,
considerando = 1,7.3

20. 12. Quanto vale x ?

21. 13. Calcule o perímetro do retângulo,
considerando =1,7.3

22. 14. Calcule o perímetro da figura,
considerando =1,7.3

23. 15. Calcule a soma dos catetos do triângulo
retângulo da figura, sabendo que AB=10 e
cos=α=3 .
5

24. um observador coloca-se a 30m de distância
e assim o observa segundo um ângulo de 30º,
conforme mostra a figura. Calcule a altura do
edifício medida a partir do solo horizontal.

25. 17. Observe a figura:
a) Qual é o comprimento da rampa?
b) Qual é a distância do início da rampa ao barranco?

26. 18. Qual era a altura desse pinheiro?