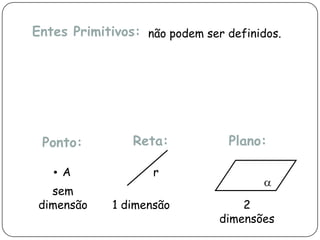
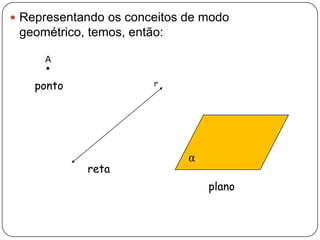
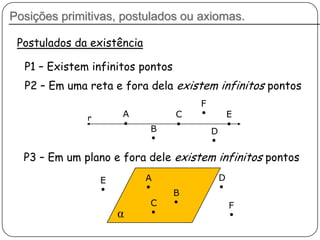
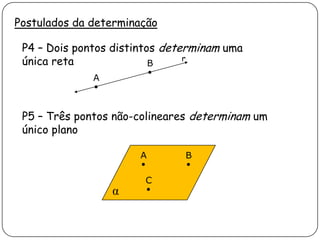
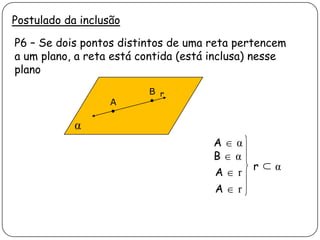
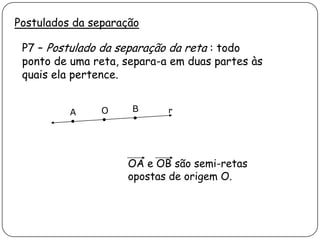
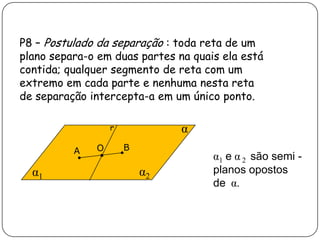
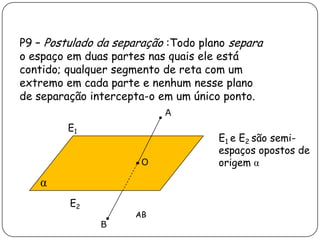
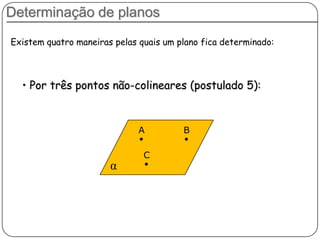
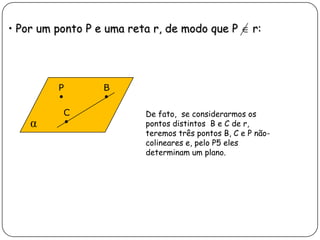
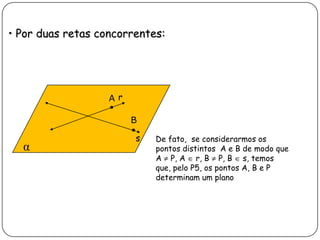
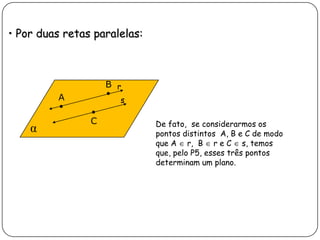
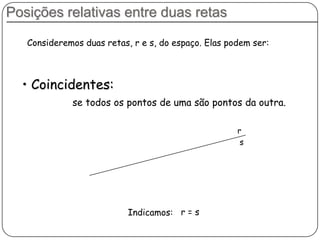
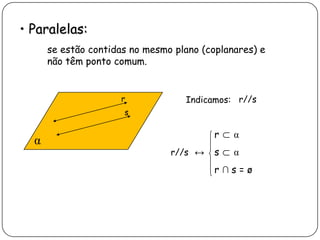
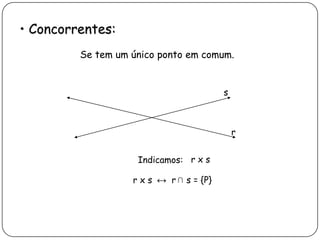
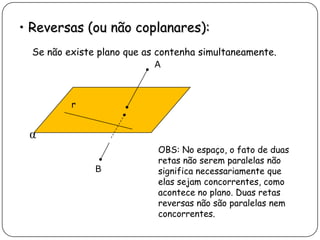
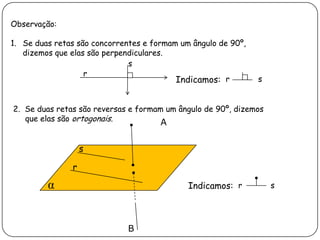
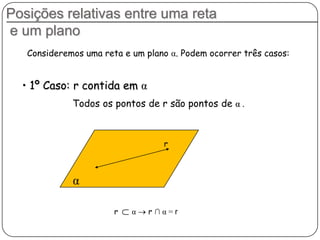
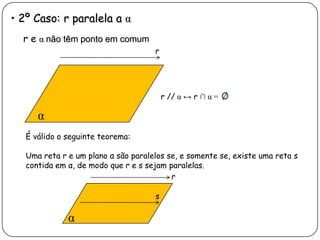
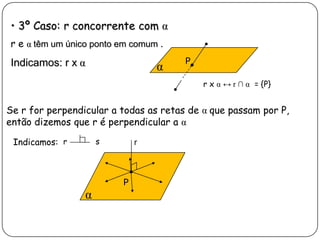
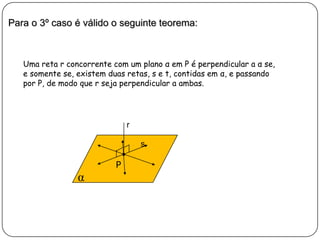
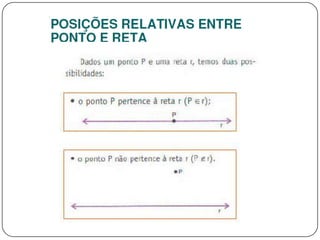
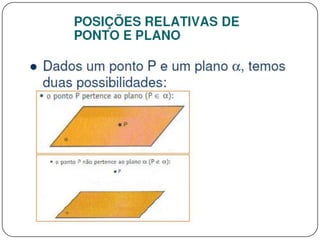
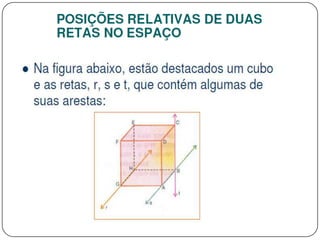
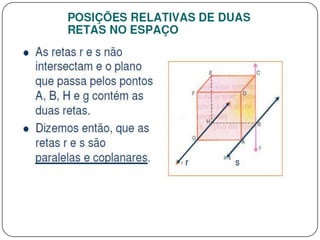
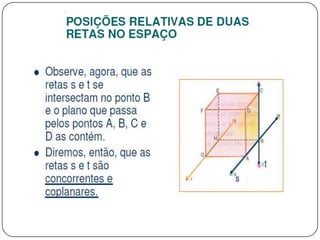
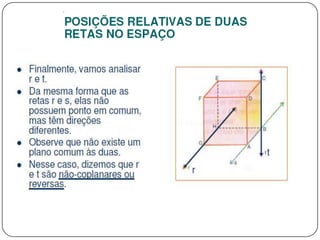
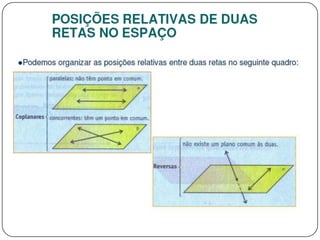
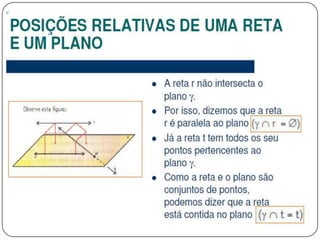
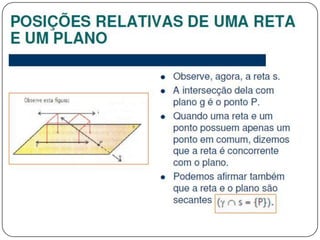
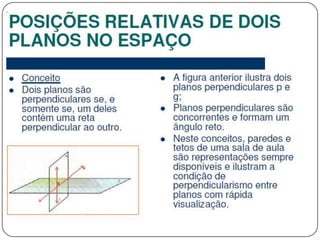
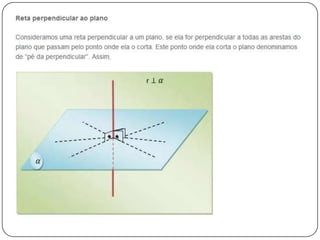
1) O documento descreve conceitos primitivos da geometria como ponto, reta e plano e suas propriedades. 2) Apresenta postulados da geometria de posição sobre a existência, determinação e separação de pontos, retas e planos no espaço. 3) Discorre sobre posições relativas entre retas e entre reta e plano, podendo ser coincidentes, paralelas, concorrentes ou reversas.

1. Conceitos primitivos
Geometria de Posição
Professora Rosana Quirino

2. Entes Primitivos: não podem ser definidos.
A
Ponto:
r
Reta: Plano:
sem
dimensão 1 dimensão 2
dimensões

3. Postulado: propriedade que não possui
demonstração.
Teorema: propriedade que possui
demonstração.

4. Conceitos primitivos
 A partir do mundo real, matemáticos da
antiguidade, como Euclides (séc. III a.C.)
estabeleceram entes com os quais
construíram a geometria. Três desses
entes destacam-se por serem
conhecidos intuitivamente. São eles: o
ponto, a reta e o plano.

5. O Ponto
 Olhando-se a noite para um céu estrelado
vêem-se as estrelas, que, intuitivamente,
podem ser consideradas pontos. Em
geometria, o ponto, elemento concebido sem
dimensão, massa nem volume, é uma noção
primitiva.

6. A Reta
 Suponha agora que fosse possível esticar,
indefinidamente e nos dois sentidos, um fio
de elástico. Em nossa imaginação, e apenas
nela, visualizaríamos o que chamamos de
reta. Em geometria, o conceito de reta –
concebido intuitivamente – também é uma
noção primitiva.

7. O Plano
 Considere o tampo liso de uma mesa, sem
nenhum tipo de fresta ou ondulação. Esse
tampo possibilitaria a visualização concreta
de um plano. Entretanto, o conceito
geométrico de plano implica que, por
intuição, ele seja entendido ilimitadamente
em todas as direções. Plano é uma noção
primitiva.

8.  Representando os conceitos de modo
geométrico, temos, então:
A
ponto r
reta
α
plano

9.  A proposição usada por Hilbert (1862 –
1943), e normalmente adotada por nós, é a
seguinte:
• Os pontos são indicados por letras
maiúsculas (A, B, C etc.).
• As retas são indicadas por letras
minúsculas (r, s, t etc.).
• Os planos são indicados por letras gregas
(α,β,γ etc.).

10. Posições primitivas, postulados ou axiomas.
Postulados da existência
P1 – Existem infinitos pontos
P2 – Em uma reta e fora dela existem infinitos pontos
A C E
DB
F
P3 – Em um plano e fora dele existem infinitos pontos
α
A
B
C
E
F
D
r

11. Postulados da determinação
P4 – Dois pontos distintos determinam uma
única reta r
A
B
P5 – Três pontos não-colineares determinam um
único plano
α
A B
C

12. Postulado da inclusão
P6 – Se dois pontos distintos de uma reta pertencem
a um plano, a reta está contida (está inclusa) nesse
plano
α
r
A
B
A α
B α
A r
A r
r α
∩

13. Postulados da separação
P7 – Postulado da separação da reta : todo
ponto de uma reta, separa-a em duas partes às
quais ela pertence.
A BO r
OA e OB são semi-retas
opostas de origem O.

14. P8 – Postulado da separação : toda reta de um
plano separa-o em duas partes na quais ela está
contida; qualquer segmento de reta com um
extremo em cada parte e nenhuma nesta reta
de separação intercepta-a em um único ponto.
α1 α2
r
OA B
α
α1 e α 2 são semi -
planos opostos
de α.

15. P9 – Postulado da separação :Todo plano separa
o espaço em duas partes nas quais ele está
contido; qualquer segmento de reta com um
extremo em cada parte e nenhum nesse plano
de separação intercepta-o em um único ponto.
α
E1
E2
A
B
O
E1 e E2 são semi-
espaços opostos de
origem α
AB

16. Posições relativas entre duas retas
Consideremos duas retas, r e s, do espaço. Elas podem ser:
se todos os pontos de uma são pontos da outra.
• Coincidentes:
r
s
Indicamos: r = s

17. • Paralelas:
se estão contidas no mesmo plano (coplanares) e
não têm ponto comum.
α
r
s
Indicamos: r//s
r//s ↔
r α
s α
r ∩ s = ø
∩∩

18. • Concorrentes:
Se tem um único ponto em comum.
r
s
Indicamos: r x s
r x s ↔ r s = {P}∩

19. • Reversas (ou não coplanares):
Se não existe plano que as contenha simultaneamente.
α
A
B
r
OBS: No espaço, o fato de duas
retas não serem paralelas não
significa necessariamente que
elas sejam concorrentes, como
acontece no plano. Duas retas
reversas não são paralelas nem
concorrentes.

20. Observação:
1. Se duas retas são concorrentes e formam um ângulo de 90º,
dizemos que elas são perpendiculares.
Indicamos:
r
s
r s
2. Se duas retas são reversas e formam um ângulo de 90º, dizemos
que elas são ortogonais.
α
A
B
r
s
Indicamos: r s

21. Determinação de planos
Existem quatro maneiras pelas quais um plano fica determinado:
• Por três pontos não-colineares (postulado 5):
α
A B
C

22. • Por um ponto P e uma reta r, de modo que P r:
α
P B
C De fato, se considerarmos os
pontos distintos B e C de r,
teremos três pontos B, C e P não-
colineares e, pelo P5 eles
determinam um plano.

23. • Por duas retas concorrentes:
α
s
r
De fato, se considerarmos os
pontos distintos A e B de modo que
A P, A r, B P, B s, temos
que, pelo P5, os pontos A, B e P
determinam um plano
A
B

24. • Por duas retas paralelas:
α
r
sA
B
C De fato, se considerarmos os
pontos distintos A, B e C de modo
que A r, B r e C s, temos
que, pelo P5, esses três pontos
determinam um plano.

25. Posições relativas entre uma reta
e um plano
Consideremos uma reta e um plano α. Podem ocorrer três casos:
Todos os pontos de r são pontos de α .
• 1º Caso: r contida em α
α
r
r α r ∩ α = r
∩

26. • 2º Caso: r paralela a α
r e α não têm ponto em comum
α
r // α ↔ r ∩ α =
r
É válido o seguinte teorema:
Uma reta r e um plano α são paralelos se, e somente se, existe uma reta s
contida em α, de modo que r e s sejam paralelas.
α
r
s

27. • 3º Caso: r concorrente com α
r e α têm um único ponto em comum .
Indicamos: r x α α
P
r x α ↔ r ∩ α = {P}
Se r for perpendicular a todas as retas de α que passam por P,
então dizemos que r é perpendicular a α
Indicamos: r s
α
r
P

28. Para o 3º caso é válido o seguinte teorema:
Uma reta r concorrente com um plano α em P é perpendicular a α se,
e somente se, existem duas retas, s e t, contidas em α, e passando
por P, de modo que r seja perpendicular a ambas.
α
r
P
s